500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

I would like to begin today with a few simple definitions of terms that appear in number theory problems on the SAT. All too often I have students attempting SAT math problems from the College Board Blue Book without even knowing what some of these terms mean. So here are a few essential definitions that you should make sure you are very familiar with.

Definitions:

The integers are the counting numbers together with their negatives.

…,-4, -3, -2, -1, 0, 1, 2, 3, 4,…

The positive integers consist of the positive numbers from the above list.

1, 2, 3, 4,…

Next we have prime numbers.

A prime number is a positive integer that has exactly two factors (1 and itself). Here is a list of the first few primes:

2, 3, 5, 7, 11, 13, 17, 19, 23,…

Note that 1 is not prime. It only has one factor.

A little trick:

Here is a quick trick for determining if a large number is prime: take the square root of the integer and check if the integer is divisible by each prime up to this square root. If not, the number is prime.

For example let’s try to figure out if 3001 is a prime number. Note that when we take the square root of 3001 in our calculator we get approximately 54.8. Now with our calculators we divide 3001 by 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, and 53 (all the prime numbers below 54.8). Since none of these are integers, 3001 is prime.

The Fundamental Theorem of Arithmetic

The fundamental theorem of arithmetic says “every integer greater than 1 can be written “uniquely” as a product of primes.”

The word “uniquely” is written in quotes because prime factorizations are only unique if we agree to write the primes in increasing order.

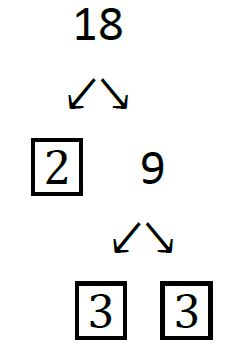
For example, 6 can be written as 2 · 3 or as 3 · 2. But these two factorizations are the same except that we changed the order of the factors. To make things as simple as possible we always agree to use the canonical representation. The word “canonical” is just a fancy name for “natural,” and the most natural way to write a prime factorization is in increasing order of primes. So the canonical representation of 6 is 2 · 3. As another example, the canonical representation of 18 is 2 · 3 · 3. We can tidy this up a bit by rewriting 3 · 3 as 3². So the canonical representation of 18 is 2 · 3². If you are new to factoring, you may find it helpful to draw a factor tree. For example here is a factor tree for 18:

To draw this tree we started by writing 18 as the product 2 · 9. We put a box around 2 because 2 is prime, and does not need to be factored anymore. We then proceeded to factor 9 as 3 · 3. We put a box around each 3 because 3 is prime. We now see that we are done, and the prime factorization can be found by multiplying all of the boxed numbers together. Remember that we will usually want the canonical representation, so write the final product in increasing order of primes.

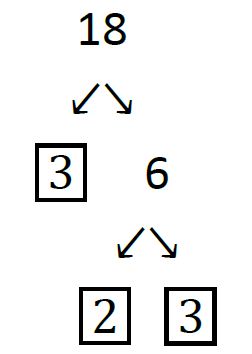
By the Fundamental Theorem of Arithmetic above it does not matter how we factor the number – we will always get the same canonical form. For example, here is a different factor tree for 18:

For practice, why don’t you try to draw a factor tree for 6137? Note that this is much more challenging than any number you will have to factor on the SAT. I’ll have the solution for you next week, so we can compare notes then. Remember, I am not looking for artistic merit – just make your factors clear in your drawing.

How many prime numbers are there?

This is going off on a bit of a tangent, but there are an infinite number of prime numbers. This was first proved by the ancient Greek mathematician Euclid.

Interestingly, the largest prime number found so far is  2^57,885,161 – 1. That’s a number with 17 million digits! I dare you to find the next one greater than that.

In the meantime, if you want to learn mathematical strategies to efficiently answer SAT math questions, I would suggest that you take a look at my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Speak to you soon!

Differences of Large Sums

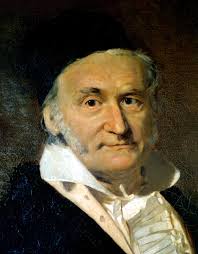
The College Board sometimes likes to put seemingly difficult problems on the SAT where you are asked to find two large sums and then subtract them.

These problems always remind me of a little story about a young boy named Karl Gauss. The story actually directly relates to the strategy I will be discussing, so it’s worth taking this little detour.

The Boy Karl Gauss

In a math class, a teacher set her students to a task to keep them busy for a few minutes.

In an attempt to keep the class quiet, the teacher asked the students to take out a piece of paper and add up the integers from 1 to 100 by hand.

The teacher was hoping for the students to painstakingly write down 1, 2, 3, 4, 5 etc… to 100, and then add the numbers together to get an answer. The teacher knew that this problem would take some time to complete as she, herself, took several minutes to get the answer.

However, one of her students, Karl, handed the teacher a piece of paper with the correct answer almost immediately. In the top left corner of the sheet, he had neatly written 5,050.

Nothing else.

Surprised that the student had the correct answer so quickly, the teacher asked how he did it.

“Oh, this was really easy” said Karl, “1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, 4 + 97 = 101… and so on. I could see that there are 100 pairs of numbers that add up to 101. So I multiplied 101 by 100 to get 10,100. I then divided by 2 because I added each number twice. So I wrote down the answer 5050.”

Let’s take one last look at Karl’s computation in an easy to read format as we will be using this format to solve SAT problems in just a moment.

    1   +   2   +  3   + … + 100
100 + 99  + 98  + … +  1
101 + 101 + 101 + … + 101

101 + 101 + 101 +…+ 101 = 100(101) = 10,100

10,100/2 = 5050

We are going to simulate Karl Gauss’s method above to get the answer to some seemingly difficult SAT math questions quickly and without making careless computational errors. Don’t worry – I will explain everything step by step.

This method is best understood with examples So let’s jump right in with SAT problems.

Example 1:

1. If x denotes the sum of the integers from 10 to 70 inclusive, and y denotes the sum of the integers from 80 to 140 inclusive, what is the value of y – x?

First, we write out each sum formally and line them up with y above x.

  80 + 81 + 82 + … + 140
10 + 11 + 12 + … + 70

Next subtract term by term.

  80 + 81 + 82 + … + 140
10 + 11 + 12 + … + 70
70 + 70 + 70 + … + 70

Now notice that we’re adding 70 to itself 70 – 10 + 1 = 61 times (by the fence-post formula – see last week’s blog post). This is the same as multiplying 70 by 61. So we get (70)(61) = 4270.

Example 2:

2. Let x ♦ y be defined as the sum of all integers between x and y. For example, 1 ♦ 4 = 2 + 3 = 5. What is the value of (60 ♦ 900) – (63 ♦ 898)?

As above, we write out each sum formally, line them up so that the numbers match up, and then subtract term by term.

     61 + 62 + 63 + 64 + … + 897 + 898 + 899
          64 + … + 897 
61 + 62 + 63 + 0 + …  … + 0 + 898 + 899

So the answer is 61 + 62 + + 63 + 898 + 899 = 1983.

Note that in each of the above problems, the numbers were lined up in different ways. It is usually pretty clear how to line up the numbers properly.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

Speak to you soon!

Fence-posts in Advanced SAT Math Problems

It’s been a few weeks since I have provided you with some mathematical content, as I’ve been spreading the word on the release of my new book: The SAT Prep Official Study Guide Math Companion. Make sure you click on the below picture if you need detailed solutions to the problems from the ten practice tests in the College Board’s Blue Book.

Today I want to get a little more specific than usual and discuss a math concept that can be used to solve certain types of problems that appear every now and then on the SAT. Tutors tend not to spend much time (if any) helping students prepare for this type of problem as it seldom appears. But if you want an 800, then you want to be able to recognize all problem types and be able to answer them correctly (and quickly!).

This problem type involves what I like to call “Fence-Posting,” a technique that allows us to count the number of integers in a consecutive list.

The Fence-post Formula

The number of integers from a to b, inclusive, is b – a + 1.

The word inclusive means that we include the extreme values. For example, if we want to count the integers from 1 to 3, inclusive, we can easily see that there are 3 of them. Note that we do include the extreme values 1 and 3. Using the fence-post formula we get 3 – 1 + 1 = 3.

The most common error when attempting to count the integers in a list is to simply subtract the smallest value from the largest value (without adding 1). Note that in the previous example, this would give an incorrect answer of 2.

As another simple example, let’s count the number of integers from 5 to 12, inclusive, in two ways – directly and by fence-posting. First directly – the integers from 5 to 12 are 5, 6, 7, 8, 9, 10, 11, 12, and we see that there are 8 of them. Now using the fence-post formula we have 12 – 5 + 1 = 8. Note that the computation 12 – 5 gives an incorrect answer of 7.

If you ever happen to forget this little formula test it out on a small list of numbers as I just did in the two examples above. But it’s nice to have this one committed to memory so that it is there for you when you need it.

Let’s take a look at a couple of examples where we can use fence-posting to obtain an answer efficiently.

Example 1:

1. Set X contains only the integers 0 through 180 inclusive. If a number is selected at random from X, what is the probability that the number selected will be greater than the median of the numbers in X?

So first of all we need to find out how many integers there are in the set X. By the fence-post formula there are 180 – 0 + 1 = 181 integers in this set.

The median of the numbers in set X is 90 (note that in a set of consecutive integers the median is equal to the average of the first and last integer). Again, by the fence-post formula, we see that there are 180 – 91 + 1 = 90 integers greater than the median.

From this we see that the desired probability is 90/181 ~ 0.4972375691.

So we grid in .497. (Note that this is a grid-in question because I have not provided answer choices).

Remember with grid in problems, we have only four slots available. We can simply truncate the final answer that we get in our calculator to fit in the four slots.

Example 2:

2. How many numbers between 72 and 356 can be expressed as 5x + 3, where x is an integer?

This problem is more complicated than the first example, but we can use fence-posting to solve this one too: Let’s start by guessing x-values until we find the smallest and largest values of x satisfying 72 < 5x + 3 < 356. Since we have 5(13) + 3 = 68 and also 5(14) + 3 = 73 we see that 14 is the smallest value of x satisfying the inequality. Since 5(70) + 3 = 353 and 5(71) + 3 = 358, the largest value of x satisfying the inequality is 70. It follows by fence-posting that the answer is 70 – 14 + 1 = 57.

Note that we also used the strategy of taking a guess to solve this problem. I discussed this strategy in a previous blog post. You can find that information by clicking on the link.

Algebraic Solution:

Although I am not a fan of students using algebra on the day of the SAT, it is true that we could have also found the two extreme x-values algebraically:

72 < 5x + 3 < 356
69 < 5x < 353
69/5 < x < 353/5
13.8 < x < 70.6
14 ≤ x ≤ 70

We get the last inequality because x must be an integer. Notice that this last inequality is not strict. For those of you not familiar with this piece of math lingo, an inequality that is not strict means that it is ‘less than or equal to’ rather than just ‘less than’.

Next week, I will be showing a quick method for computing differences of large sums. You will also see how the fence-post formula can sometimes be useful in solving these types of problems. Click the following link to read this article: Differences of Large Sums

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I hope all is well with you today.

I was with a friend of mine who was telling me a story about her son in his junior year of high school who is SAT obsessed.

This student has every problem in every available big brand name SAT prep book memorized. He can recite paragraphs of text relating to SAT concepts that are discussed in these prep guides.

However, when this student took the SAT and got his results he was shocked. And not shocked in a good way!

You see, even though this student studied and put in time (probably too much time in my opinion) he never studied by practicing problems that are exactly like those on the actual SAT. He was ‘unfamiliar’ with the  look/style of the problems. 

I, of course, recommended that my friend’s son practice problems found within the The Official Guide.

No matter who is helping students with their SAT prep – tutors, teachers, or even other students – we all agree that the practice tests in The Official Study Guide should be used during their preparation.

The reason for this is simple. The Official Guide, also known as the Blue Book, is the only SAT prep product written by The College Board, the same organization that creates the SAT. The 10 tests in the Blue Book contain problems similar to those that you can expect to see on test day.

Any student that is not practicing problems from the Blue Book is putting themselves at a serious disadvantage.

However, you may have noticed the distinct lack of detailed solutions with The College Board’s problems in the tests.

Although the problems in the blue book are fantastic, the solutions provided by the College Board are not so fantastic. In the actual Blue Book there are no solutions at all, and if you do have access to the College Board’s solutions then you have only a single solution (often involving time sapping complicated algebra) that may not be the best way to solve to the problem.

Before my students commence tutoring sessions with me they always complain that The Official Guide has no solution explanations.

This is why I have created The Complete Official SAT Study Guide Companion.

This book contains explanations for all the math problems in the tests in the Blue Book. My solutions are detailed, and often I show how problems can be solved in several different ways so that you can choose the methods that suit you the most on test day. 

Remember, unlike The College Board, I am not a fan of using tedious, time-consuming and complicated algebra to solve a question. My methods are quick, efficient and (dare I say!) fun. I use mathematical tricks, tips and strategies to solve problems and I detail my methods in a step by step way.

I have been tutoring SAT math for over 13 years now, and none of my students use complex methods to solve problems on test day. My students would much rather use the quickest and simplest method to solve a problem and then use the time they have left over to “recheck” their answers using a different method to make sure that they have not made a careless error.

My students are always happy with the score they get in SAT math!

You should certainly be using College Board practice tests to make sure that you are implementing strategies correctly and using your time wisely under pressure. You can easily use this guide to provide explanations to any problems you get incorrect during your practice. By reattempting the problems you get wrong with my methods, you will see how you have internalized more efficient ways to solve problems correctly.

This means you can expect a higher score on results day!

Problems to all 10 tests are here in this guide. You also get access to my solutions to the problems in the Official DVD Test.

All in all, I have provided you with the most effective and efficient solutions to every problem in 11 tests.

Click on this link to take you to the product page – you can buy an electronic or paperback version of the book.

Feel free to ask me any questions you may have about this new book.

All the best!

Hi all.

You may be aware that I have a YouTube channel featuring many of my SAT Math videos offering advice, tips and strategies as well as other test prep related material.

I would love for you to take a look at the channel and even subscribe to it so that you can be updated whenever I upload new content.

Below are all the videos I have made and uploaded to the channel so far. I am showing you these here in case you have not seen them before. A lot of the content in these videos is aimed at students who want advice to achieve an 800 score.

This first video details preparing for the SAT math in the correct way. This is actually my most popular video with the most views. It seems to me that YouTube viewers must like the content in this video. I hope you find this (and all the others) useful.

This second video shows the important SAT math formulas you need to remember to get a perfect or near perfect score in SAT math.

Next I have this video on how to make sure that you get those last few math questions on any math section of the SAT correct.

The video below is one of my first videos showing an SAT math strategy. The styling is different in this video compared to the others, but the content is just as good!

Here I am completing an SAT math section. I have done this to show how easy it is to finish the test with plenty of time left over to check your answers.

And here I am completing another SAT math section.

And here is the final SAT math test section being completed.

Next, I have a video providing advice on how best to take the SAT for an 800 in math.

This video is all about my latest series of books 28 SAT Math Lessons to Improve Your Score in One Month. These books are rather unique and so I felt as if I should explain what these SAT math prep books are and who they are for.

Whenever you are taking expert advice from someone you should always make sure that they are qualified to be giving such advice. This next video describes my SAT math qualifications and credentials.

Students often incorrectly use their first instinct to answer SAT problems on test day. Here I explain that using your gut instinct can be a dangerous method to answer SAT math problems – ultimately lowering your SAT math score.

Finally, here is video giving the pros and cons of paying for a professional SAT math prep course.

I hope you enjoy these videos and find them useful. I would really appreciate if you would ‘like’ each of the videos by pressing the thumbs up button, share them, and make comments. Of course, please subscribe to the channel as well.

Until next week!

Two weeks ago I mentioned that I wrote and released my detailed solutions to Test 8 in the College Board’s Official Guide (also known as the Blue Book). I released Test 8 first because my brand new laptop crashed just as I was completing Test 7. I’m still hurting from the loss, and do not want to re-write Test 7 just yet!  See last week’s post for details if you didn’t read it.

Today I would like to announce that I have completed the solutions to Test 9 in the College Board’s Blue Book. The Official SAT Study Guide Companion – Test 9 is now available.

As usual, this guide  often gives several different ways to solve a given problem. I always say that being able to solve any specific SAT math problem is not that important. After all, you will never see that specific problem on an SAT again. It is more important to learn as many techniques as possible that can be applied to a wide range of problems. This is what you will get in my solution guides.

The link to purchase this book is here. Solutions to tests 2,3 ,4, 5, 6 and 8 can also be found through the same link. These are available for $3 each. The solutions to the College Board’s Blue Book – Test 1 can be downloaded for free by subscribing to the 800 Initiation – a free online SAT math e-mail course that I know will boost your SAT scores on test day provided you internalize the advice and review the problems within it.

Turn Wrong Answers Into Right Answers

Today I want to discuss a common mistake that students make which leads to bad preparation.  The type of mistake I am about describe is especially common during preparation for standardized tests, and in particular the SAT (also note that this information is just as relevant to the ACT).

Although many SAT problems can be very difficult to solve, it is usually not very hard to understand the solutions. After getting a problem wrong, a good student will go over the solution until they understand it completely. Very often, however, the same student will misinterpret understanding the solution as being able to reproduce the solution on their own.

If after a student gets a question wrong I explain the correct way to do it and they understand my explanation, then more than likely if I ask them to solve the question 5 minutes later they will be able to do so. But it is important to realize that this does not mean that they will be able to solve a similar question (or even the exact same question) two months later during their SAT.

Understanding a solution and being able to reproduce it using short term memory does not necessarily lead to long term retention.

So what is the answer? How does a student make sure that they do not make the same mistake on their actual exam that they had made during their preparation?

The answer is quite simple.

During preparation, anytime you get a question wrong mark it off. You should have a special mark that is easy to see and recognize. Students of mine use stars, spirals or even sad faces.

Yes, the marks above were created in MS Paint! But I’m sure, you get the idea…

It is very important to mark off every single question you have gotten wrong regardless of the reason. Even if the only reason you got it wrong is because you accidentally hit a wrong button in your calculator or even if you got it wrong because you just misread one of the numbers in the problem – mark it off anyway! It is very easy to say “oh that was just a silly mistake – I know how to do this,” and then to never look at that problem again. This is a huge mistake. Let me repeat this one more time. Mark off EVERY question you get wrong. Every question! Not just the ones you do not understand. Every single one!

You must reattempt each question you get wrong at least four days later. Do not reattempt the problem the next day, or the day after that. If you only wait one or two days you may be getting the problem correct for the wrong reason. The question is too fresh in your mind. You need time to forget how you solved it. This way you can be sure that you understand how to solve the problem, as opposed to simply recalling the solution.

If you get the problem correct you can “unmark” it and remove it from the list of problems you need to redo. If you get it wrong again, then leave it marked off and reattempt it again at least four days later. You need to keep reattempting each problem you get wrong with at least four days between attempts. You should only stop reattempting a problem once you get it completely correct on your own without recalling exactly how the problem was solved. Only then can you know for certain that you have internalized the technique necessary to solve that problem.

If you follow the advice I have given here, then every time you get a problem right that you had previously gotten wrong, you will be one step closer to a perfect score.

I want you to treat this message in the same way as I recommend you treat a question you answer incorrectly. Come back to this in 4 days time. Re-read and internalize. I am certain you will benefit from the information here if you make it a part of your long term memory..

And if if you would like lots of practice problems I suggest you take a look at my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

The title of this post may seem a bit strange, but I do have an explanation for you… In the future I may look back on the following story and laugh, but right now that’s not the case.

I have been releasing my detailed solutions to the tests in the College Board’s Official SAT Study Guide in numerical order. I planned to write Test 1 first and Test 10 last.

My master plan was going well. I released the solutions to SAT 1 through 6 and I had just completed Test 7.

But then my laptop crashed. Not just crashed as in “froze” or “displayed the blue screen of death” – my laptop’s innards were utterly destroyed; cut down in the prime of its life – it was only a month old!

Anyway, upon restarting my computer, my data was gone. All wiped away. Nothing left. All my previous work disappeared. My so-close-to-completion solution guide for Test 7 was gone. Not only did I lose the work I put into my Get 800 SAT math books, but I also lost a month’s worth of research related to my work at Hofstra University.

The ironic thing is that I just started backing up my data when this happened!

I took my laptop to an expert to see if the data could be recovered, but there was no hope. Accepting that you have lost all your data is a a tough pill to swallow. But I quickly moved on to creating my solutions to Test 8. I do not want to rewrite my solutions to Test 7 just yet, as I am still mourning the loss of the work I had put in to creating it.

So today I would like to announce that I have completed the solutions to Test 8 in the College Board’s Blue Book. “The Official SAT Study Guide Companion – Test 8” is now available.

This guide that I have written often has several different ways to solve a given problem. I always say that being able to solve any specific SAT math problem is not that important. After all, you will never see that specific problem on an SAT again. It is more important to learn as many techniques as possible that apply to a wide range of problems. This is what you will get in my solution guides.

Here is the link to purchase the solutions to Test 8 of the College Board’s Blue Book. Solutions to tests 2, 3, 4, 5 and 6 can also be found through the same link. These are all available for $3 each. The solutions to Test 1 can be downloaded for free by subscribing to the 800 Initiation – a free online SAT math e-mail course that I know will boost your SAT scores on test day provided you internalize the advice and review the problems within it.

Changing Averages To Sums

A problem involving averages often becomes much easier when we first convert the averages to sums. We can easily change an average to a sum using the following simple formula.

Sum = Average · Number

Many problems with averages involve one or more conversions to sums, followed by a subtraction.

Examples:

Try to answer the following question using this strategy. Do not check the solution until you have attempted this question yourself.

1. The average (arithmetic mean) of three numbers is 100. If two of the numbers are 80 and 130, what is the third number?

               (A)   70
               (B)   80
               (C)   90
               (D)   100
               (E)   110

In this case we are averaging 3 numbers. So the Number is 3. The Average is given to be 100. Thus, the Sum of the 3 numbers is 10 · 3 = 300. Since two of the numbers are 80 and 130, the third number is 300 – 80 – 130 = 90, choice (C).

Got it? Well here is another, slightly more advanced, problem where this technique is useful:

2. The average of x, y, z  and w is 15 and the average of z and w is 11. What is the average of x and y?

The Sum of x, y, z and w is 15 · 4 = 60. The Sum of z and w is 11 · 2 = 22. Thus, the Sum of x and y is 60 – 22 = 38. Finally the Average of x and y is 38/2 = 19.

Notice how we actually used the formula “Sum = Average · Number” twice here. For those of you that require further clarification, here are the calculations in more detail.

If you liked this article, please share it with your Facebook friends:

Changing Averages To Sums

More On Remainders

Welcome to the third and final part of this thread on remainder problems. In the first part we discussed some calculator algorithms for finding remainders. You can review that article here: SAT Remainder Problems – Part 1

Last week we discussed the cyclical nature of remainders. You can review that article here: SAT Remainder Problems – Part 2

I decided to spend three blog posts on this subject because many of my students in a mid-level scoring range seem to have a difficult time with SAT remainder questions.

Solution To Last Week’s Remainder Problem

So where were we? I left you with an SAT math problem to solve using the information I provided regarding the cyclical nature of remainders. Let’s find out how you did.

The problem again:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

We first find the least positive integer greater than 4 that is divisible by both 6 and 8. This is the least common multiple of 6 and 8 which is 24.

We now simply add the remainder.

24 + 4 = 28.

Thus, the answer is 28.

If you don’t know how to find the least common multiple of two numbers, it’s okay. You can just let your TI-84 calculator do it for you. In your calculator press MATH, scroll right to NUM, and press 8 for lcm. Then type 6,8) and you will get an output of 24. So lcm(6,8)=24.

For more information on the lcm, see the following article: Greatest Common Divisor (GCD) And Least Common Multiple (LCM)

Remainders In Disguise

The College Board loves to put their remainder problems in disguise. In fact, most remainder problems on the SAT do not even have the word “remainder” in the question! So how can you be expected to know when to find a remainder? The answer is quite simple. If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Remember this and you will recognize a remainder problem every time. In fact, this is such a key point I am going to repeat this in bold for you!

If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Let’s take a look at a standard example of such a question:

Cards numbered from 1 through 2013 are distributed, one at a time, into nine stacks. The card numbered 1 is placed on stack 1, card number 2 on stack 2, card number 3 on stack 3, and so on until each stack has one card. If this pattern is repeated, each time beginning with stack one, on which stack will the card numbered 2013 be placed?

So this is the end of this three part thread on remainders. If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

See you soon!