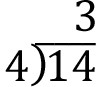500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Remainder Problems

Last week I introduced the idea of solving remainder problems without using long division. We may as well take advantage of the fact that we can use our T-84 calculator on the SAT to solve seemingly difficult SAT math questions with ease. If you haven’t done so already, please read part 1 before continuing with this article: SAT Remainder Problems – Part 1

Solution To Last Week’s Problem

In the last post I left you with a cliffhanger of a problem to solve with your calculator. Below is the solution. Let’s see if you got the problem correct and which method you used to solve the problem.

Here is the question again:

What is the remainder when 15,216 is divided by 73?

If you recall I gave three methods to solve such a problem, the first of which is by using long division. Since this post is about solving problems without using long division, let’s skip that method and jump straight to the much quicker and more efficient calculator algorithms – great for use on test day!

Method 2 – First Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Multiply the integer part of this answer by the divisor:

73*208 = 15,184

Step 3: Subtract this result from the dividend to get the remainder:

15,216 – 15,184 = 32.

And here is an alternative:

Method 3 – Second Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Subtract off the integer part of this result:

ANS – 208 ~ .438

Step 3: Multiply this result by the divisor:

73*ANS = 32.

Did you get this problem correct? Which method did you use? Try using both methods and then choose the one that you will be most comfortable with on the day of the SAT. And remember: the best way to get comfortable with a new technique is to practice with it!

When we divide 3 by 3 we get a quotient of 1 and a remainder of 0. In other words,

3 = 3(1) + 0.

When we divide 4 by 3 we get a quotient of 1 and a remainder of 1. In other words,

4 = 3(1) + 1.

Now we have to be careful. When we divide 6 by 3, the quotient is now 2 and the remainder is 0. That is, 6 = 3(2) + 0.

Now let’s see if you can apply this information to an actual SAT math problem – the type you can expect to see in the College Board’s Blue Book. Here is a nice medium difficulty problem I like to give to my own SAT math students:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

Do you know how to go about solving this? You can find the answer in part 3 of this article here: SAT Remainder Problems – Part 3

You may want to check out my 28 SAT Math Lessons Series for more SAT math remainder problems. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

And now read part 3 of this article here: SAT Remainder Problems – Part 3

I’m sitting here with a Japanese friend of mine who is a math teacher and also has a nice website offering free math help to Japanese high school students.

I’m looking at the kind of math that an equivalent 10^th grade student would have to study (1st grade in Japan) – and it’s mind blowing. It’s the kind of material that an SAT Mathematics Level 2 Subject Test student would have to master to get a top score in the exam.

I just wanted to share his website with you: 13^th Note. 

You probably will not be able to read much of it, as it is in Japanese. But I did want to spread the word for the good work that he is doing – in Japan, the math books that one has to learn from are set by the Government and are even more dull than the College Board’s books. His free books are becoming very, very popular in Japan as they are easy to understand and very concise.

I feel that the work we are doing is very similar, albeit in different countries.

Perhaps if you are a Japanese student in America, you can take a look at this site and see how different the subjects are.

Keep up the good work, Kutomi!

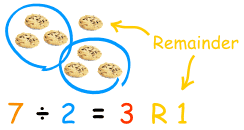SAT Remainder Problems

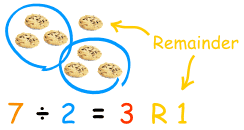
For the next few weeks I would like to help you to understand SAT math problems involving remainders. This will be the first of three such articles.

SAT math problems with remainders seem to give students a difficult time and limit SAT scores. This is mostly because a fundamental step in solving the problem is often missed – performing long division.

You cannot solve a remainder problem by simply dividing in your calculator. There are, however, calculator algorithms that can give you the answer very quickly. We will talk about these a bit later in this post.

A common error that students make is to perform a division calculation on their TI-84 calculator or similar device, and simply take the first number after the decimal point and use this digit as the answer to the problem. This will usually result in a wrong answer.

Example:

Suppose we are asked “Find the remainder when 14 is divided by 4.”

In your calculator, 14/4 = 3.5.

Penciling the number 5 as your answer would be incorrect – seriously incorrect. This “5” is actually part of the answer to the question “What is 14 divided by 4?” But it has nothing to do with the remainder.

Students that are currently scoring in the mid-range in PSAT/SAT math seem to have the biggest problem with remainder questions. Many cannot perform long division correctly, and some do not even realize that long division is needed. This keeps many students from getting their SAT scores to the next level.

Let’s take a look at how we can solve the problem of finding the remainder when 14 is divided by 4 in three different ways. This problem may seem very basic for some of you, but let’s go over it anyway to make sure we have a strong foundation before solving more difficult remainder problems.

Method 1 – Long Division: So 4 goes into 14 three times with 2 left over. In other words, 14 = 4(3) + 2. So we see that the remainder when we divide 14 by 4 is 2.

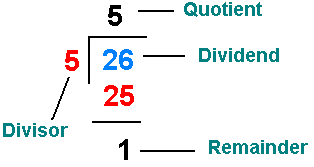
Let’s break this down step by step:

Count the number of groups of 4 objects that can be formed from 14 objects. Place this number over the 4 that is inside the division symbol.

Multiply this resulting  number 3 by the divisor 4. Place this number below the 4 that is inside the division symbol.

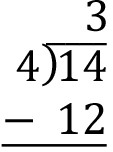
Subtract the resulting number 12 from the dividend 14.

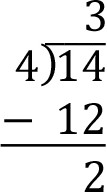
The quotient 3 appears above the division symbol and the remainder 2 appears at the bottom.

Below is a visual representation of 14 divided by 4. In the figure below we are grouping 14 objects 4 at a time. Note that we wind up with 3 groups (the quotient) and 2 extra objects (the remainder).

Method 2 – First Calculator Algorithm:

Step 1: Perform the division in your calculator: 14/4 = 3.5

Step 2: Multiply the integer part of this answer by the divisor: 4*3 = 12

Step 3: Subtract the above result from the dividend to get the remainder:

14 – 12 = 2.

Method 3 – Second Calculator Algorithm:

Step 1: Perform the division in your calculator: 14/4 = 3.5

Step 2: Subtract off the integer part of this result: ANS – 3 = .5

Step 3: Multiply this result by the divisor: 4*ANS = 2.

Note that these calculator algorithms work exactly the same no matter how large the numbers are that you are dividing.

Exercise:

As an additional exercise you should try to find the remainder when 15,216 is divided by 73 by using one of these calculator algorithms. Figure out which of the two algorithms you prefer. You can find solutions here: SAT Remainder Problems – Part 2

More information on remainders can be found in my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

For part two of this article please click the following link: SAT Remainder Problems – Part 2

Those of you that have been following this blog will have noticed that I have been furiously releasing new SAT math products that will help you to increase your score on test day and to improve your overall application to get into college.

Today I would like to announce that I have completed the solutions to Test 6 in the College Board’s Blue Book. “The Official SAT Study Guide Companion – Test 6” is now available.

Maybe you are wondering why I am working so hard to create these solutions. Well, in the blue book there are no solutions provided at all, and if you do have access to the College Board’s solutions then you have only a single solution which, in my opinion, may not always be the best way to solve that problem. The College Board’s solution is often a very ‘mechanical’ way to solve the problem without the use of any of my  efficient and effective strategies (i.e. mathematical hints, tips and tricks).

This guide that I have written often has several different ways to solve a given problem. I always say that being able to solve any specific SAT math problem is not that important. After all, you will never see that specific problem on an SAT again. It is more important to learn as many techniques as possible that apply to a wide range of problems. This is what you will get in my solution guides.

The link to purchase this book is here. Solutions to tests 2,3 ,4, and 5 can also be found through the same link. These are all available for $3 each. The solutions to the College Board’s Blue Book – Test 1 can be downloaded for free by subscribing to the 800 Initiation – a free online SAT math e-mail course that I know will boost your SAT scores on test day provided you internalize the advice and review the problems within it.

Helping Others

This week I would like to share an approach to improving your own SAT math score by helping other students to improve their score. Every student I tutor is encouraged to pass along their knowledge to other students as there are many benefits for both students.

I believe that if you want to take yourself to the next level without too much effort, simply teach what you already know to someone else. Helping someone else to learn something new requires a much deeper understanding of the underlying material than simply having superficial knowledge of the subject matter. By engaging with someone else with less understanding than you, you will find that you often have to be creative with your explanations in order to get the other person to acquire a complete understanding of what you are trying to teach. This will force you to think about the subject matter in different ways. A nice side effect of this process is an overall improvement in both your current knowledge and your critical reasoning skills.

This is especially useful for SAT prep and also mathematics in general where it often helps to solve problems by thinking “outside the box.” By helping others to understand how to solve problems you will be forced to review the tips, tricks and techniques that you already know. This will help you to internalize them more quickly so that you will be able to more easily identify problems where a specific strategy will be useful, and you will become more adept at using them.

Ways To Help Others

There are several ways to help others:

1. You can find students in your school (or elsewhere) whose current score levels are below yours and offer to tutor them in a formal setting.
2. You can let other students know that whenever they are stuck on an SAT problem, they should see you, and you will be happy to do your best to provide a solution for them.
3. You can answer questions on forums where students post SAT questions. Feel free to answer questions in the Get 800 SAT/ACT Prep Forum, and post the questions that you are having trouble with yourself.

Benefits Of Helping Others

And now here are some of the benefits of helping others with their SAT prep:

1. You will be forced to review SAT material that you have already learned.
2. You will be more likely to internalize strategies that you are familiar with so that they’re application becomes faster and more reliable.
3. You will begin developing a deeper understanding of the underlying mathematics leading to a higher level of mathematical maturity.
4. You will improve your problem solving and critical reasoning skills at a faster rate than by simply learning new material.
5. You will be providing a service to others by helping them improve their SAT scores.

So get out there and offer your tutoring services to someone who needs your help. You will be providing an invaluable service to another person. They will certainly be grateful for your help.

Of course, this applies not only to improving your SAT math score but to anything in life that you want to perform well in: be it college, sports, or even just playing video games!

And what about the fact that primarily you’re actually helping yourself to get into your college of choice? Well, we’ll keep that as our little secret.

This week I had a question posted up on my Facebook Timeline by a student in regards to being able to increase one’s math score by the next SAT in March.

In the same question the student states that most of his errors are just “careless” mistakes. I redirected him to my article on avoiding careless mistakes, but let me just repost our whole conversation here as it has information relevant to a lot of other students. I hope you find this useful…

Student: Hi Dr. Steve, I feel as if I have hit a plateau because I can’t really score higher than a 710. I always do practice sections from the College Board Blue Book and miss around 1-2 questions per section. The questions I get incorrect are usually medium questions and not hard. I believe I make careless mistakes… What should I do? I also tend to do A LOT of practice sections. Could this negatively affect my score? My exam is on March 9th and I would like to score 750+(preferably an 800). Is increasing from a 700 to 750+ in just weeks impractical?

Dr Steve: The increase you are looking for is definitely possible. It sounds like all of your prep right now consists of doing practice tests from the College Board’s Blue Book. You should stop this and start prepping in a more efficient way. Now I also need to know what you mean by the word “usually” when you say that you usually get medium questions incorrect. Does that mean on any given practice test you get more medium questions wrong, or that you practically never get hard questions wrong at all? This distinction is important. Let me start with a few suggestions to get you on the right path.

1. If you haven’t done so already, read my article on avoiding careless errors here.
   
2. Go back through all the practice tests you took and start posting up the questions you got wrong here on my Facebook wall. Also explain what the error you made was, no matter how silly or careless you think the errors were. We can then discuss several different ways to solve these problems and how to avoid these errors in the future.
3. Are you proficient in the really basic strategies such as plugging in answer choices, picking numbers, taking guesses, etc. If not, then you need to start practicing lots of problems using these strategies even if you know more efficient ways to solve them. The Intermediate Course from my “28 Lessons” series emphasizes these strategies in a systematic way. The Advanced Course reviews these strategies very quickly in the first lesson, but still gives solutions using these techniques throughout the book. In your case, if you did decide to get one of these, I would probably recommend the Advanced, but make sure you are practicing solving as many of these problems as you can using both basic and advanced strategies. If you choose to continue using only the materials you already have, then again, make sure you are practicing both basic and advanced techniques.
4. Let me emphasize that as you practice solving SAT math questions, try to solve each one in 2 to 4 ways. Possibly using a basic strategy, a more advanced strategy, the way you would do it in school, and/or the quickest way you can think of. Remember – you will never see any specific math problem that you do on your SAT – it’s more important to learn techniques than it is to solve a specific problem.
5. To really improve your score do every problem you get wrong about once per week until you get that question right on your own without making any “careless” errors. Make sure you wait at least several days before reattempting a problem you have gotten wrong. You don’t want to get it right because you recall the mistake you made. You want to get it right because you are no longer falling into the trap you previously fell for.

Student: Well I can confidently say that I know most, if not all, of your strategies (I bought your book and went through the level 5 questions of your book since I got all level 4 questions correct) and that I know all the math involved in most, if not all problems. Out of all the sections I have ever taken, I have only been totally clueless in only like 2 problems (I’ll try to find them; they are questions from the online Free practice test by the College Board). By “usually” I mean I practically never get a hard question wrong unless I make a silly mistake or get tricked, which is quite rare. Since I know not to follow my intuition on hard questions, I tend to check over my work like 2-3 times. On medium questions, however, I tend to work really fast through them. The reason I do this is because it can sometimes take me quite a while to solve some hard questions even if I’m using strategies. Another thing, the way I attack the SAT math section is by just going once through the whole section. Even if I feel that I got all the answers right, I somehow made a mistake in one without noticing. I have question: What is the maximum amount of questions I can miss and still get a 750 or higher? Or does that change from test to test?

Oh wow, I looked back to a problem that I was totally clueless on and solved it in less than 30 seconds.

Dr Steve: To guarantee a 750 you can only get 2 questions wrong (omitting them or getting them wrong is equivalent here since the .5 loss will be rounded up). However, the scaling at the high end is very inconsistent, so depending on the overall difficulty of the test you may be able to omit 1 or possibly even 2 more.

Based upon your last response, here are a few suggestions:

1. Have you watched the 3 videos of me completing the 3 math sections of an SAT from the College Board Blue Book in about 9 minutes each? I think it would be useful to just observe my process. Especially pay attention to how I move quickly but how I do not rush and I even look over my work pretty often before moving on. It is very important not to rush through easier questions. Don’t try to emulate what I’m doing – you need to develop speed at your own pace – just observe.
2. For at least the next week focus on one problem at a time (no full practice tests). Go back and pick out problems that have taken you more than 1 minute. Really take the time to work out the problem several different ways and try to really internalize these methods. Then pay special attention to the one that was quickest.
3. In about a week take another practice test and really focus on NOT RUSHING. Pace yourself correctly meaning if you are working on a problem for about 30 seconds and you’re still confused by it, mark it off and move on – come back to it later – don’t worry – you’ll get to it, and as long as you’re pacing yourself correctly you will have plenty of time to finish the section, go back and work on the ones you skipped, and you may even have several minutes to go back and redo many of the problems one more time. You may want to read this article.”

The student replied that he would look at the additional material.

I wish him and all other students taking the March 2013 SAT the best of luck in achieving an exceptional math score..

Teachers and tutors may have their own personal philosophies, but there is one thing that they all agree on – every student that wants to improve their score in SAT math should be attempting the questions from the practice tests given in “The Official SAT Study Guide” by the College Board.

Despite this, my colleagues and I have always wanted more from the infamous blue book. The problems in the Official Guide are fantastic – they are exactly the types of questions you will encounter on the SAT. The explanations to the problems, however, are not so fantastic. In the blue book there are no explanations at all, and if you do have access to the College Board’s solutions then you have only a single solution which, in my opinion, may not always be the best way to solve that problem. This is why I have created “The Official SAT Study Guide Companions.”

The Official SAT Study Guide Companions contain solutions to the SATs in the Official SAT Study Guide. As usual, I give simple, efficient, in-depth solutions to each of these problems, and most problems are solved using several different methods.

I have created the guides in response to the teachers, tutors and students that have found the College Board’s solutions to these problems to be unsatisfactory.

Tests 1, 2, 3 and 4 are already available; Test 1 is available for free by subscribing to my free 12 part SAT math prep email course. If you have not subscribed to this course called the 800 Initiation, you are missing out an a great opportunity to improve your score. And Tests 2, 3 and 4 can be found here.

I have just released my solutions to Test 5, which is available as an electronic download for $3.

I’m working as quickly as I can to get the next 5 tests out for you to use – keep an eye on this space for more solutions to help you to, ultimately,  get a higher score. You can expect test 6 to be available in the next month or so.

Let’s keep in touch!

This book will guide students in a step by step fashion to increase their SAT math scores within one month – providing the lesson schedule is adhered to.

I have created this book to provide quick results to students that want to dramatically improve their scores in a short period of time.

If you are currently scoring below 500 in SAT math and you wish to get to the next score level quickly and efficiently, then this new book is for you.

When this book is used by students for self study a significant rise in SAT math score will result as long as each lesson is completed and the content is internalized.

The Intermediate and Advanced versions of this book are already available, but this book is specifically designed for students that are currently scoring below 500 in SAT/PSAT Math.

After the lessons have been completed, I believe a student should get closer to a score of 600.

This book is perfect for those students that only have a limited time for study. It takes all the guesswork out of what to study. If you are familiar with my work, you know that I am extremely thorough with the solutions to problems I provide as practice. My years of experience have enabled me to create this guide that will take you to a higher SAT math score.

Click on this link to take you to the product page – you can buy an electronic or paperback version of the book for a limited time only. The electronic version of this book is only $5.

That’s right, only $5!! The usual price is $24 dollars for the electronic version, so be quick with your purchase…

Picking Numbers In Percent Problems

Last week we looked at the basic but important strategy of picking numbers. Click the following link to view that post: Picking Numbers – A Basic SAT Math Strategy

At the end of that post, I did say that we would be applying this strategy to percent problems.

When picking a number in percent problems, the best choice is usually the number 100. After all, the word percent literally translates to “out of 100.”

Example 1:

Let’s take a look at an SAT problem involving percents:

There are b bricks that need to be stacked. After k of them have been stacked, then in terms of b and k, what percent of the bricks have not yet been stacked?

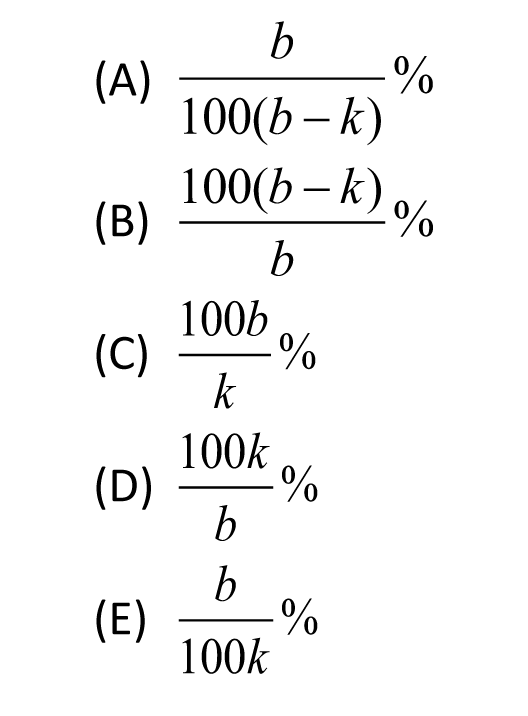
Since this is a percent problem let’s choose 100 for the total number of bricks. So we have b = 100. For k, let’s choose 25, so that 25 bricks have been stacked, and so that means 100 – 25 = 75 have not been stacked. Since we started with 100 as our total, 75% of the bricks have not been stacked. Remember to put a big, dark circle around 75%. We make the substitutions b = 100 and k = 25 into each answer choice.

 

We now compare each of these percents to the percent that we put a nice big, dark circle around. Since (A), (C), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice (B).

As I always like to stress: (B) is not the correct answer simply because it is equal to 75%. It is correct because all four of the other choices are not 75%. You absolutely must check all five choices!

Example 2:

Now let’s look at a percent problem without answer choices. Even though there is no variable in the problem to pick a number for, we can still use the number 100 to solve the problem quickly and easily.

If Matt’s weight increased by 30 percent and Lisa’s weight decreased by 20 percent during a certain year, the ratio of Matt’s weight to Lisa’s weight at the end of the year was how many times the ratio at the beginning of the year?

Again, 100 is the magic number – let’s choose 100 pounds for both Matt’s weight and Lisa’s weight at the beginning of the year. Matt’s weight at the end of the year was then 100 + 30 = 130 pounds and Lisa’s weight at the end of the year was 100 – 20 = 80 pounds. We then have that the ratio of Matt’s weight to Lisa’s weight at the beginning of the year was 100/100 = 1, and the ratio of Matt’s weight to Lisa’s weight at the end of the year was 130/80 = 13/8. We can therefore grid in 13/8.

Side note: 13/8 is equal to 1.625 as a decimal. Thus, we can also grid in 1.62 or 1.63. We get 1.62 by truncating the decimal, and 1.63 by rounding the decimal. Truncating is better because less thought is involved. Note that if you grid in 1.6 the answer will be marked wrong.

So remember the magic number ‘100’ whenever you see a problem with the word “percent” in it… but as always, practice makes perfect – so find more of these problems, such as those found in my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Picking Numbers

The strategy of “picking numbers” works on a wide range of different SAT math problems in all topics and difficulty levels. It can often be used to make a difficult problem much easier to understand, and if you are careful in its use, you will usually get the answer without too much trouble. The idea is simple – replace the unknowns in the problem with specific values.

Here are some guidelines when picking numbers.

1. Pick a number that is simple but not too simple. In general you might want to avoid picking 0 or 1 (but 2 is usually a good choice).
2. Try to avoid picking numbers that appear in the problem.
3. When picking two or more numbers try to make them all different.
4. Most of the time picking numbers only allows you to eliminate answer choices. So do not just choose the first answer choice that comes out to the correct answer. If multiple answers come out correct you need to pick a new number and start again. But you only have to check the answer choices that have not yet been eliminated.
5. If there are fractions in the question a good choice might be the least common denominator (lcd) or a multiple of the lcd.
6. In percent problems choose the number 100.
7. Do not pick a negative number as a possible answer to a grid-in question. This is a waste of time since you cannot grid a negative number.
8. If your first attempt does not eliminate 4 of the 5 choices, try to choose a number that is of a different “type.” Here are some examples of types:
   1. A positive integer greater than 1.
   2. A positive fraction (or decimal) between 0 and 1.
   3. A negative integer less than -1.
   4. A negative fraction (or decimal) between -1 and 0.
9. If you are picking pairs of numbers try different combinations from (8). For example you can try two positive integers greater than 1, two negative integers less than -1, or one positive and one negative integer, etc.

Remember that these are just guidelines and there may be rare occasions where you might break these rules. For example sometimes it is so quick and easy to plug in 0 and/or 1 that you might do this even though only some of the answer choices get eliminated.

Examples

Okay, so let’s try solving an SAT math practice problem by picking numbers:

1. For nonzero numbers a, b, and c, if c is three times b and b is 1/5 of a, what is the ratio of a² to c²?
               (A)   9 to 25
               (B)   25 to 9
               (C)   5 to 9
               (D)   5 to 3
               (E)   3 to 5

Looks scary? This SAT problem is actually pretty easy if you pick numbers.

Let’s choose a value for a, say a = 5. Then b = 1, c = 3, and therefore the ratio of a² to c² is 25 to 9, choice (B).

Simple, right? Maybe a bit too simple? You can of course solve this SAT math problem algebraically as well, but an algebraic solution is more likely to lead to careless errors, and in this problem will actually take more time than picking numbers.

Here is one more  SAT math problem for more practice:

2. If a = 3^b and b = c + 4 , what is a/27 in terms of c?
               (A)   c + 1
               (B)   3^c
               (C)   3^c+1
               (D)   3^c + 1
               (E)   3^c + 2

Using the same method as above, let’s pick a number for c, say c = 2. It follows that b = 2 + 4 = 6. So using our calculator, a = 3⁶ = 729. We then have a/27 = 729/27 = 27. Put a nice big, dark circle around this number so that you can find it easily later. We now substitute a 2 for c into each answer choice and use our calculator.

We now compare each of these numbers to the number that we put a nice big, dark circle around. Since (A), (B), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice (C).

Remember by picking a number, we can only eliminate answer choices: (C) is not the correct answer simply because it is equal to 27. It is correct because all four of the other choices are not 27. You absolutely must check all five choices!

You can see how powerful picking numbers can be to solve SAT math problems. Follow the guidelines I have provided above and you should be solving more difficult SAT math problems with ease. In next week’s post we will see how to apply the strategy of picking numbers to problems involving percents. Click the following link to view that post: Picking A Number To Solve Percent Problems

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Until then…