500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Students seem to have a lot of trouble remembering the basic rules of exponents. On the SAT, you can often do problems involving exponents by using some basic strategies that avoid using these rules altogether. Using the exponent laws, however, usually leads to the quickest solutions. Students that are trying to get an SAT math score higher than 700 will want to become more proficient in using these laws of exponents. Here is a basic review.

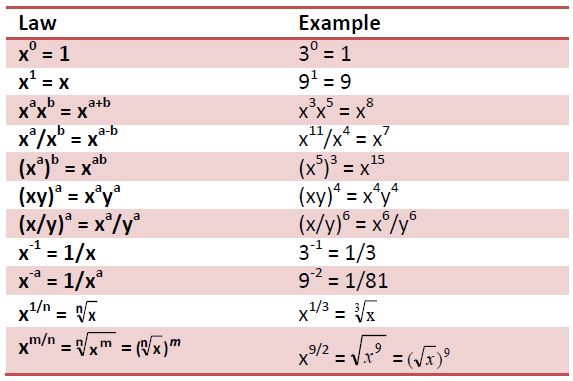
Now let’s try a level 5 question:

If y = 7^x, which of the following expressions is equivalent to 49^{x  −} 7^x+2  for all positive integer values of x?

 

The first 5 people to comment on this post with a correct answer will get an electronic copy of 28 SAT Math Lessons to Improve Your Score in One Month.

I would also like to see how you got to the answer, so please show your calculations!

Answers have to be received on this blog post by Sunday, November 18, 2012. (Answers will remain hidden until the 18th).

Winners can have a choice of the intermediate course or, the not yet released (!!), advanced course. The intermediate course is for students that are currently scoring between 500 and 600 in SAT math and want to get to the next  score level. The advanced course is for students scoring above 600 and ideally would like to get a perfect score of 800.

Good luck!

 

Plugging In Answer Choices

In many SAT math problems you can get the answer simply by trying each of the answer choices until you find the one that works. Unless you have some intuition as to what the correct answer might be, then you should always start with choice (C) as your first guess. The reason for this is simple. Answers are usually given in increasing or decreasing order. So very often if choice (C) fails you can eliminate two of the other choices as well.

There are a few exceptions to this rule. If the word least appears in the problem, then start with the smallest number as your first guess. Similarly, if the word greatest appears in the problem, then start with the largest number as your first guess.

Examples

Let’s take a look at two SAT math problems – one where we start with choice (C) and one where we do not.

1. When each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a side of the original square?

               (A)   3
               (B)   4
               (C)   5
               (D)   6
               (E)   7

Let’s start with choice (C). If the original length of a side of the square is 5, then the length becomes 8 when we increase it by 3. The original square has an area of 5²= 25 and the new square has area 8² = 64. So the area is increased by 64 – 25 = 39 square inches. Thus, we can eliminate choice (C), and most likely (A) and (B) as well.

We next try choice (D). We have 6² = 36, 9² = 81 and 81 – 36 = 45. Thus, the answer is choice (D).

Here is an algebraic solution for those of you that really want to see it.

Thus, the answer is choice (D).

For this particular question, I prefer the solution by starting with choice (C) to the more tedious and confusing algebraic solution.

Now for the second example.

2. What is the largest positive integer value of k for which 3^k divides 18⁴?

               (A)   2
               (B)   4
               (C)   6
               (D)   7
               (E)   8

Pull out your calculator. Since the question has the word “largest” in it, we will start with the largest answer choice which is choice (E), and we will divide 18⁴ by 3⁸. We type 18^4 / 3^8 into our calculator and the output is 16. Since 16 is an integer, the answer is choice (E).

Note that all five answer choices give an integer, but 8 is the largest positive integer that works.

Here is a direct solution for those of you who really want to see it.

The prime factorization of 18 is 18 = 2·3². Therefore:

18⁴ = (2·3²)⁴ = 2⁴(3²)⁴ = 2⁴3⁸.

From this prime factorization it should be clear that 3⁸ divides 18⁴, but 3⁹ does not.

Again, for this particular question, most students will prefer the easier solution of starting with choice (E) (the largest answer choice) to the more confusing algebraic solution.

More SAT Math Practice Problems

More information on this extremely useful strategy, as well as many more problems to practice with, can be found in my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Speak to you soon!

SAT/ACT Myths: 4 Techniques That Will Not Work!

You may have gotten advice from various sources regarding the SAT, the ACT, or standardized tests in general. Here are some common pieces of advice that you should not follow.

1. When in doubt choose choice (C): This strategy does not work on the SAT or ACT  (and it is unlikely to work on any standardized test). Standardized tests are carefully created so that all answer choices are equally likely. You should always take a guess on multiple choice questions if you do not know the answer (after eliminating as many choices as you can). At this point feel free to choose (C) if it has not been eliminated, but there certainly isn’t any advantage to doing so.

Look out for a future blog post about starting with choice (C) as a time saving strategy.

2. Go with your first instinct: This strategy is okay for the first few math problems in any given section, since they are meant to be easy and straightforward. But medium and especially hard questions are designed to trick you. Therefore your first instinct may very well be to fall into the exact trap they have set for you. You should be especially cautious if your “intuition” gets you an answer very quickly on one of the higher numbered problems in a section.

3. The best way to study for the SAT or ACT is by doing lots of practice tests: Although taking practice tests is not a bad thing, it is not the most efficient way to increase your performance on a standardized test. The best way to increase your SAT score is by doing just a few SAT problems a day over a period of several months, and similarly for the ACT.

Taking a practice test will be most effective if you make sure that you go over all the problems that you got wrong, understand your mistakes, and (most importantly) you periodically redo the problems you got wrong until you can do each one yourself without referring back to the solution.

When doing this, remember to focus on problems that are within and slightly above your current ability level. If you’re struggling with Level 2 Geometry problems, then you shouldn’t be worrying about Level 4 and 5 Geometry problems at all.

I am by no means implying that you should not take any practice tests. You should take at least four before the actual exam (as stated above), but this is not the time that you are improving your mathematical and reasoning ability.

4. Take the test during an “off” month because it’s easier. There is no evidence that suggests that you will get a better score on the SAT or ACT if you take it in one month as opposed to another month. Take the test when you are ready, preferably after you have done at least three months of consistent preparation. Try to take the test for the first time in your junior year.

Best of luck on whichever exam you choose to take!

If you are looking for a tutor in New York City you may want to check out Prima Tutoring.  Prima’s tutors will travel within the 5 boroughs and Long Island. They offer tutoring in a variety of subjects including SAT math, and their SAT tutors are encouraged to use my books.

I am really pleased that a tutoring company as professional as Prima Tutoring is using my books with their SAT students.

Gaining Mathematical Maturity

Today I would like to talk about mathematical maturity and how it relates to your performance in SAT math. Although there is no single agreed upon definition of mathematical maturity, I would define it as “one’s ability to analyze, understand, and communicate mathematics.”

There is no strict measure of mathematical maturity, but let’s examine what various levels of mathematical maturity might look like:

• Level 1: These students can do basic high school math when taught in a classroom setting. Students at level 1 can solve basic algebra and geometry problems by following the procedures that were taught to them. If such a student were asked, “Why does this work?” they will not be able to verbalize a satisfactory answer. Most high school students are at this level.

• Level 2: These students can learn basic mathematics without any outside help. Students at level 2 can read an algebra or precalculus book on their own  and can probably explain basic mathematics to other students. If shown how to do a problem, they will be able to solve problems that are similar using the same strategy. These students would have no problem in a Calculus course.

• Level 3: These students can learn advanced mathematics on their own. Students at level 3  can not only do problems, but can also explain why the methods they are using work. They can often solve problems in several different ways and develop their own techniques for solving problems. These students will be able to solve problems of a type that they have never seen before as long as they know the appropriate definitions and relevant background material.

These “levels” are just here to illustrate a point. It is often hard to pinpoint the exact level of a student. Some students naturally have a higher level of mathematical maturity than others. For example, students taking AP Calculus usually have a higher level of mathematical maturity than a student in remedial algebra. As such, the AP Calc student is more likely to do better in math on the SAT.

Simply knowing more mathematics is not enough to guarantee a higher level of mathematical maturity. An AP Calculus student does not have a higher level of mathematical maturity simply because they know more math. It is because they have been attempting problems that require a higher level of thinking.

The good news is that mathematical maturity can be increased. Doing so will greatly improve your problem solving ability as well as increase your math score on the SAT. Here are a few ways you can increase your level of mathematical maturity.

• Do SAT math problems. If you can currently only solve Level 1 geometry problems, and a month from now you can solve Level 2 geometry problems, then guess what—you have increased your level of mathematical maturity. So keep doing SAT problems a level above your current ability until the day of the test. If you only have about 3 months before your test, then this is the method you should employ most, if not exclusively.

• Learn some mathematics by yourself. This may seem contrary to what has already been stated—but it is not. Knowing more mathematics will probably not raise your score very much, especially if the math is handfed to you. But the process of learning mathematics will increase your mathematical maturity. What kind of math should you learn? It does not matter! Pick something you find the most enjoyable, and try to learn it on your own. If you get stuck, then ask for help—but developing the skill to learn math yourself will definitely increase your mathematical maturity. This strategy is more long term and you should consider it if you have 6 months or more before your SAT.

• Attempt difficult math problems. There are a lot of challenging math problems out there that only require the math that you already know. There are math magazines (yes, I know these sound like a lot of fun!), websites, and books full of problems. Pick a few and struggle with them. Just trying difficult problems and developing strategies will increase your mathematical maturity, even if you never solve a single one on your own. Also, solving problems using the advanced methods that are described in the books I have written will boost your level of mathematical maturity.

I can still remember the day I got back my first real analysis homework as a first year graduate student at Rutgers University. I received a 62. This is by far the lowest grade I had ever received in mathematics. The worst part was that I had spent many hours on this homework, and I thought that it was completely correct. I remember approaching my teacher explaining that I never received such a low math grade, begging for him to tell me what to do. But he did not have an answer for me. I was on my own.

That whole first year of graduate school was a struggle. I wound up with B’s in most of my classes despite working harder than I had ever worked in my life. I was  unprepared for how difficult graduate school was, especially after receiving a 4.0 Math GPA as an undergraduate with very little effort.

This was quite disheartening and I thought that there was no way I would be able to do mathematical research and get my Ph.D. I just was not smart enough.

But an interesting thing happened during my second year. Apparently my hard work paid off. All of a sudden nothing seemed difficult anymore — I was back at the top of my class. Despite the fact that I was taking even harder classes than the previous year I was breezing through them with very little effort.

All of a sudden I was able to read advanced graduate texts on my own and do the problems at the end of each section without any help from others. What happened? Did I all of a sudden accumulate a massive amount of mathematical knowledge. The answer is no. In fact, this would not have helped. The mathematical language in my new classes was actually quite different from what I had learned the previous year.

What happened is that by struggling so hard the year before with little to no help from others, I managed to increase my level of mathematical maturity. Things that I did not stand a chance of understanding just a year earlier now made perfect sense. Other students were now coming to me for help, and I was able to help every single one of them. To think just a year earlier I was considering dropping out because it was just too hard. What a shame that would have been.

My level of mathematical maturity had to take several more jumps before I would graduate. Mathematical research is highly sophisticated and requires a clever mind that is willing to think in unconventional ways. The one thing that my years at graduate school have taught me is that anyone is capable of doing anything that they set their mind to.

Just don’t give up and you will persevere!

P.S. If you are preparing for the SAT you might want to take a look at the Get 800 collection of SAT math books.

Good luck for those who are taking the SAT tomorrow.

If you are feeling anxious or nervous about the test, please see this article on eliminating test-taking anxiety.

In this article there are tips on:

1. Being prepared for the SAT
2. Increasing confidence
3. Knowing how to take the SAT correctly
4. Taking practice SATs
5. Getting yourself in the test taking ‘zone’
6. Staying out of your own way
7. Warming up the morning of the SAT
8. Releasing tension right before the test.

I wish you all the best.

If you want to take the SAT in October, then today is your last day to register.

Today is also the last day to make changes to your previous registration.

To register direct via the College Board click on this link.

As always, I wish you all the best of luck with your SAT prep leading up to test day. If you do need extra help then please take a look at the articles I have written to help you prepare for SAT math.

In addition to this blog, there are many other free resources I offer, such as the 800 Initiation, my 12 part 6 week free email prep course. Also check out my Facebook and Twitter pages. There is a lot of great SAT math info on these pages too.

In my book The 32 Most Effective SAT Math Strategies, I suggest “picking numbers” as a method for solving many types of SAT math problems. Using this particular strategy on SAT math problems is not always the quickest way to arrive at a solution, but it does have several points in its favor:

(1) By replacing variables with specific numbers a difficult SAT problem often becomes much easier to understand.

(2) If you do your computations carefully, this method will help you avoid careless errors and will guide you to the correct solution quite easily.

(3) This is the perfect “fallback method.” Use it on problems that are a bit above your ability level to squeeze out a few more correct answers on the SAT.

PWN The SAT has written a nice blog post on this particular strategy (although he refers to it as “plugging in”). Check out the example he provides and attempt to solve it in two ways. First try to solve it by “plugging in,” and then try to solve it algebraically (the way you would do it in school). Compare your answers to the solutions he provides.

I am planning to begin posting articles on the various SAT math strategies that are described in my book – so keep an eye out for those! Until then, keep plugging in those numbers to get a higher SAT math score.

General Graphing Calculator Advice for the SAT/ACT

• I always recommended that you use a TI-84 or comparable graphing calculator for the SAT or ACT.
• It is important that you are comfortable with your calculator on test day, so make sure that you are consistently practicing with the calculator you plan to use.
• Make sure that your calculator has fresh batteries the day of the test. Nobody will supply a calculator for you if yours dies.
• You may have to switch between DEGREE and RADIAN modes during the test. If you are using a TI-84 (or equivalent) calculator press the MODE button and scroll down to the third line when necessary to switch between modes.

Graphing Calculator Features You Should Know for the SAT/ACT

Below are the most important things you should practice on your graphing calculator.

(1) Practice entering complicated computations in a single step, and know when to insert parentheses. In general, there are 4 instances when you should use parentheses in your calculator. Around numerators of fractions Around denominators of fractions Around exponents Whenever you actually see parentheses in the expression

• Around numerators of fractions
• Around denominators of fractions
• Around exponents
• Whenever you actually see parentheses in the expression

Examples: We will substitute a 5 in for x in each of the following examples.

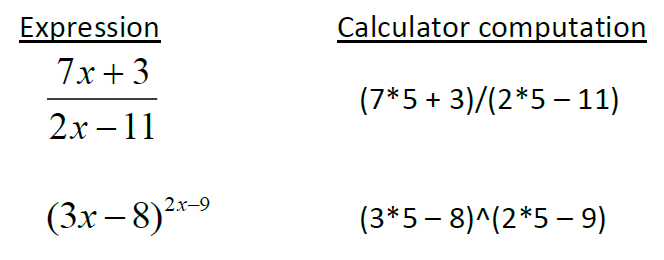
(2) Clear the screen before using it in a new problem. The big screen allows you to check over your computations easily.

(3) Press the ANS button (2^nd (-) ) to use your last answer in the next computation.

(4) Press 2^nd ENTER to bring up your last computation for editing. This is especially useful when you are plugging in answer choices, or guessing and checking.

(5) You can press 2^nd ENTER over and over again to cycle backwards through all the computations you have ever done.

(6) Know where the ,√ ,π and ^ buttons are so you can reach them quickly.

(7) Change a decimal to a fraction by pressing MATH ENTER ENTER.

(8) Press the MATH button – in the first menu that appears you can take cube roots and nth roots for any n. Scroll right to NUM and you have lcm( and gcd(.

(9) Know how to use the SIN, COS and TAN buttons as well as SIN^-1, COS^-1 and TAN^-1.

The following items are less important but can be useful.

(10) Press the Y= button to enter a function, and then hit ZOOM 6 to graph it in a standard window.

(11) Practice using the WINDOW button to adjust the viewing window of your graph.

(12) Practice using the TRACE button to move along the graph and look at some of the points plotted.

(13) Pressing 2nd TRACE (which is really CALC) will bring up a menu of useful items. For example selecting ZERO will tell you where the graph hits the x-axis, or equivalently where the function is zero. Selecting MINIMUM or MAXIMUM can find the vertex of a parabola. Selecting INTERSECT will find the point of intersection of 2 graphs.

And now it’s time to start practicing lots of SAT math problems. For this you may want to take a look at the Get 800 collection of SAT math prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

See you in a week!

Here is some basic stuff you need to remember for test day.

The full article can be found at SAT Exam Savvy.

The list includes the obvious things such as a calculator and identification, but it also contains things that you might not think of such as spare batteries for you calculator.