500 New SAT Math Problems
Just 19.99 on Amazon
Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.
The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.
The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems
If you have any questions, feel free to contact me at steve@SATPrepGet800.com
Thank you all for your continued support!
A Trick For Free Two Day Shipping
I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.
Sign Up For Amazon Prime For Free
If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.
This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.
After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.
Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.
Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:
Sign Up For Amazon Prime For Free
If you think your friends might be interested in this special offer, please share it with them on Facebook:
Thank you all for your continued support!
 |
 |
 |
 |
 |
SAT Level 5 Passport to Advanced Math Problem
Here is a difficult Passport to Advanced Math problem for the SAT. I will provide a solution soon.
Level 5 Passport to Advanced Math
g(x)=x2 + 4x – 1
h(x)=2x3 + 3x2 + x
The polynomials g and h are defined above. Which of the following polynomials is divisible by 2x – 1 ?
A) k(x) = g(x) – h(x)
B) k(x) = 12g(x) – h(x)
C) k(x) = g(x) – 10h(x)
D) k(x) = 12g(x) – 10h(x)
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
 |
SAT Level 5 Heart of Algebra Problem
Here is a hard Heart of Algebra problem for the SAT. I will provide several different solutions to this problem over the next few days.
Level 5 Heart of Algebra
A worker earns $12 per hour for the first 40 hours he works in any given week, and $18 per hour for each hour above 40 that he works each week. If the worker saves 75% of his earnings each week, what is the least number of hours he must work in a week to save at least $441 for the week?
A) 6
B) 8
C) 46
D) 47
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
SAT Level 5 Heart of Algebra Problem
Here is a hard Heart of Algebra problem for the SAT. I will provide several different solutions to this problem over the next few days.
Level 5 Heart of Algebra
A worker earns $12 per hour for the first 40 hours he works in any given week, and $18 per hour for each hour above 40 that he works each week. If the worker saves 75% of his earnings each week, what is the least number of hours he must work in a week to save at least $441 for the week?
A) 6
B) 8
C) 46
D) 47
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
Hard SAT Geometry Problem with Solution
Today I would like to solve the SAT geometry problem I posted yesterday. You can see the original post here: Hard SAT Geometry Problem
Level 5 Geometry
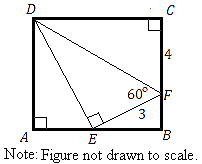
ABCD shown above is a square, m∠DFE = 60°, EF = 3, and CF = 4. What is the area of square ABCD ?
Solution: DF is the hypotenuse of a 30, 60, 90 triangle (ΔDEF). Since EF = 3, we have DF = 6.
We can now use the Pythagorean Theorem to get
DC2 = DF2 – CF2 = 62 – 42 = 36 – 16 = 20.
Notes: (1) The area of a square is A = s2, where s is the length of a side of the square.
(2) There is no need to find DC here because the area of the square is equal to DC2, and that’s what we found.
(3) The 30, 60, 90 triangle and the Pythagorean Theorem are both given to you at the beginning of each SAT math section.
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
Hard SAT Geometry Problem
Here is a hard SAT Geometry problem. Come back tomorrow for a solution.
Level 5 Geometry
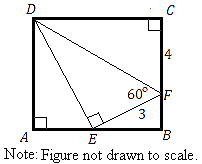
ABCD shown above is a square, m∠DFE = 60°, EF = 3, and CF = 4. What is the area of square ABCD ?
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
SAT Level 4 Passport to Advanced Math Problem with Solution
Today I would like to solve the last SAT math problem I posted. You can see the original post here: SAT Level 4 Passport to Advanced Math Problem
Level 4 Passport to Advanced Math
Let m = 2x + 7 and k = 2x – 7, and write km = cx2 + d, where c and d are constants. What is the value of c – d ?
* Solution using the difference of two squares:
km = (2x + 7)(2x – 7) = 4x2 – 49.
So, we have 4x2 – 49 = cx2 + d.
Thus, c = 4 and d = –49.
It follows that c – d = 4 – (–49) = 4 + 49 = 53.
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
SAT Level 4 Passport to Advanced Math Problem
Here is a hard Passport to Advanced Math SAT problem. Come back tomorrow for a solution.
Level 4 Passport to Advanced Math
Let m = 2x + 7 and k = 2x – 7, and write km = cx2 + d, where c and d are constants. What is the value of c – d ?
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
Inequality Word Problem for the SAT with Solutions
Today I would like to give a solution to the SAT problem from last Wednesday on Inequalities. You can see the original post here: Inequality Word Problem for the SAT
Level 5 Heart of Algebra
A worker earns $12 per hour for the first 40 hours he works in any given week, $18 per hour for each hour above 40 that he works each week. If the worker saves 75% of his earnings each week, what is the least number of hours he must work in a week to save at least $441 for the week?
A) 6
B) 8
C) 46
D) 47
* Informal solution: If $441 represents 75% of the worker’s earnings, then the worker’s total earnings is 441/0.75 = $588.
For the first 40 hours, the worker earns 12 ⋅ 40 = 480 dollars. So, the remaining amount that the worker needs to earn is 588 – 480 = 108 dollars. So, the number of additional hours above 40 that the worker will work is 108/18 = 6.
The total number of hours that the worker must work is therefore 40 + 6 = 46, choice C.
Notes: (1) We change a percent to a decimal by moving the decimal point to the left 2 places. The number 75 has a “hidden” decimal point at the end of the number (75 = 75. or 75.0). When we move this decimal point to the left two places we get .75 or 0.75.
(2) We can find the worker’s total earnings formally as follows:
We are given that 441 is 75% of the worker’s total earnings. So, we have 441 = 0.75T, where T is the worker’s total earnings. We divide each side of this equation by 0.75 to get T = 441/0.75 = 588.
(3) Be careful that you do not accidentally choose 6 as the answer. 6 is the number of hours above 40 that the worker must work. The question is asking for the total number of hours, which is 40+6.
Algebraic solution 1: Let x be the number of hours that the worker works above 40 hours. We need to solve the following inequality for x:
0.75(12⋅40 + 18x) ≥ 441
480 + 18x ≥ 441/0.75
480 + 18x ≥ 588
18x ≥ 108
x ≥ 6
So, the least number of hours the worker needs to work is 40 + 6 = 46, choice C.
Notes: (1) For the first 40 hours, the worker earns 12 ⋅ 40 = 480 dollars.
(2) For x hours above 40, the worker earns 18x dollars.
(3) using notes (1) and (2), we see that he worker earns a total of 12 ⋅ 40 + 18x = 480 + 18x dollars.
(4) We are given that 75% of the total earned must be at least 441. So, 0.75T = 441, where T = 12 ⋅ 40 + 18x (see note (2) in the previous solution).
(5) Remember that we let x represent the number of hours the worker works above 40. So, at the end, we need to add 40 to the result.
Algebraic solution 2: This time we let x be the total number of hours that the worker works, where x must be at least 40. We need to solve the following inequality for x:
0.75(12⋅40 + 18(x – 40)) ≥ 441
480 + 18x – 720 ≥ 441/0.75
18x – 240 ≥ 588
18x ≥ 828
x ≥ 46
So, the least number of hours the worker needs to work is 46, choice C.
Notes: (1) This time we are letting x represent a number greater than or equal to 40.
If x = 40, the total earnings is 12 ⋅ 40 + 18 ⋅ 0
If x = 41, the total earnings is 12 ⋅ 40 + 18 ⋅ 1
If x = 42, the total earnings is 12 ⋅ 40 + 18 ⋅ 2
Observe the relationship between x and the last number in the expression (both in bold). We subtract 40 from the x-value to get that number.
This shows that the total earnings is 12 ⋅ 40 + 18(x – 40).
(2) This time, the value that we get for x is the answer to the question.
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|
Inequality Word Problem for the SAT
Here is a hard SAT problem involving inequalities. A solution will be posted soon.
Level 5 Heart of Algebra
A worker earns $12 per hour for the first 40 hours he works in any given week, $18 per hour for each hour above 40 that he works each week. If the worker saves 75% of his earnings each week, what is the least number of hours he must work in a week to save at least $441 for the week?
A) 6
B) 8
C) 46
D) 47
Share this problem with your Facebook friends that are preparing for the SAT
If you’re preparing for the SAT, you may want to check out the Get 800 collection of SAT math books.
|
|
|
|
|
|