500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

The Discriminant of a Quadratic Equation
Part 4

Let’s continue talking about the discriminant of a quadratic equation. You can review parts 1, 2 and 3 of this discussion here:

The Discriminant of a Quadratic Equation – Part 1
The Discriminant of a Quadratic Equation – Part 2
The Discriminant of a Quadratic Equation – Part 3

Recall that the discriminant of the quadratic equation ax² + bx + c = 0 is the quantity Δ defined by

Δ = b² – 4ac

That is, the discriminant is simply the expression that appears under the square root in the quadratic formula.

Last week, I asked you to solve the following problem:

Example: Find the discriminant of x² + 4x + 8 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 4x + 8.

Make sure to try this problem yourself before reading the following solution.

Solution: In this question, we have a = 1, b = 4, and c = 8. So the discriminant is

Δ = b² – 4ac = 4² – 4(1)(8) = 16 – 32 = –16.

Since the discriminant is negative, it follows that the two roots of the quadratic equation are distinct complex numbers.

The graph of the function y = x² + 4x + 8 is an upward facing parabola that does not intersect the x-axis.

Notes: (1) In this example, we can find the two complex solutions of the quadratic equation by using the quadratic formula or by completing the square. I leave it as an exercise to show that the two solutions are –2 + 2i and –2 – 2i.

(2) Notice that the two solutions are complex conjugates of each other. This will always happen when the discriminant is negative. For more information on complex conjugates, see the following post: Complex Numbers – Division

(3) We know that the parabola opens upwards because a = 1 > 0.

(4) It’s very easy to also find the y-intercept of the parabola. We simply substitute 0 in for x into the equation. So we get y = 8. It follows that the y-intercept of the parabola is the point (0,8).

Now try the following problem which is similar to a problem found on a recent ACT:

Example: You are given the following system of equations.

dx + ey = f
y = x²

where d, e, and f are integers. For which of the following will there be more than one (x, y) solution, with real-number coordinates for the system?

A. e² + 4df < 0
B. e² – 4df < 0
C. d² – 4ef < 0
D. e² – 4df > 0
E. d² + 4ef > 0

I will post a solution to this problem tomorrow. Feel free to post your own solutions in the comments.

If you liked this article, please share it with your Facebook friends:

The Discriminant of a Quadratic Equation
Part 3

Today I would like to continue our discussion of the discriminant of a quadratic equation. You can review parts 1 and 2 of this discussion here:

The Discriminant of a Quadratic Equation – Part 1
The Discriminant of a Quadratic Equation – Part 2

Recall that the discriminant of the quadratic equation ax² + bx + c = 0 is the quantity Δ defined by

Δ = b² – 4ac

That is, the discriminant is simply the expression that appears under the square root in the quadratic formula.

Last week, I asked you to solve the following problem:

Example: Find the discriminant of x² + 8x + 7 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 8x + 7.

Make sure to try this problem yourself before reading the following solution.

Solution: In this question, we have a = 1, b = 8, and c = 7. So the discriminant is

Δ = b² – 4ac = 8² – 4(1)(7) = 64 – 28 = 36.

Since the discriminant is positive, it follows that the two roots of the quadratic equation are distinct real numbers. Furthermore, since 36 is a perfect square (6² = 36), the roots are actually rational.

The graph of the function y = x² + 8x + 7 is an upward facing parabola that intersects the x-axis at two points.

Notes: (1) In this example, we can easily find the two roots of the equation by factoring:

x² + 8x + 7 = 0
(x + 1)(x + 7) =0
x + 1 = 0        or        x + 7 =0
x = –1       or       x = –7

So the two roots are –1 and –7.

(2) We know that the parabola opens upwards because a = 1 > 0.

(3) It’s very easy to also find the y-intercept of the parabola. We simply substitute 0 in for x into the equation. So we get y = 7. It follows that the y-intercept of the parabola is the point (0,7).

Negative Discriminants

Up until now, we’ve looked at the cases where the discriminant is 0 and positive. Today let’s talk about what happens if the discriminant is negative.

If the discriminant of the quadratic equation ax² + bx + c = 0 is negative, then we wind up with a negative number under the square root in the quadratic formula. The square root of a negative number is an imaginary number. We therefore wind up with two complex solutions.

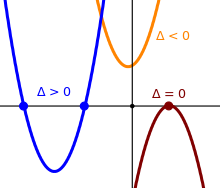
Graphically, if the discriminant is negative, the graph of the function y = ax² + bx + c is a parabola that does not intersect the x-axis.

An example is given by the yellow parabola in the image above.

Example: Find the discriminant of x² + 4x + 8 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 4x + 8.

I will post a solution to this problem tomorrow, and then discuss what happens if the determinant is negative. Feel free to post your own solutions in the comments.

If you liked this article, please share it with your Facebook friends:

The Discriminant of a Quadratic Equation
Part 2

Last week, I began discussing the discriminant of a quadratic equation. You can review that post here: The Discriminant of a Quadratic Equation – Part 1

Recall that the discriminant of the quadratic equation ax² + bx + c = 0 is the quantity Δ defined by

Δ = b² – 4ac

That is, the discriminant is simply the expression that appears under the square root in the quadratic formula.

Last week, I asked you to solve the following problem:

Example: Find the discriminant of x² + 6x + 9 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 6x + 9.

Make sure to try this problem yourself before reading the following solution.

Solution: In this question, we have a = 1, b = 6, and c = 9. So the discriminant is

Δ = b² – 4ac = 6² – 4(1)(9) = 36 – 36 = 0.

It follows that the roots of the quadratic equation are equal (in other words, there is really just one root) and rational (a fraction, where the numerator and denominator are both integers).

The graph of the function y = x² + 6x + 9 is an upward facing parabola that intersects the x-axis at one point.

Notes: (1) The unique rational root of this quadratic equation is 

x = –b/2a = –6/2 = –3.

This means that the only x-intercept of the parabola is the point (–3,0). In this case, this point also happens to be the vertex of the parabola. 

(2) We know that the parabola opens upwards because a =1 > 0.

(3) It’s very easy to also find the y-intercept of the parabola. We simply substitute 0 in for x into the equation. So we get y = 9. It follows that the y-intercept of the parabola is the point (0,9).

(4) Now that we know the x-intercepts, y-intercept, and vertex of the parabola, and we know that the parabola opens upwards, it’s very easy to sketch the graph. I leave it to the reader to draw a nice sketch.

Positive Discriminants

So far, we’ve just looked at the case where the discriminant is 0. Today let’s talk about what happens if the discriminant is positive.

If the discriminant of the quadratic equation ax² + bx + c = 0 is positive, then we wind up with a positive number under the square root in the quadratic formula. The square root of a positive number is a real number. We therefore wind up with the two real solutions

If the discriminant also happens to be a perfect square (such as 1, 4, 9, 16, etc.), then both solutions will be rational numbers.

Graphically, if the discriminant is positive, the graph of the function y = ax² + bx + c is a parabola that intersects the x-axis at two points.

An example is given by the blue parabola in the image above.

Example: Find the discriminant of x² + 8x + 7 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 8x + 7.

I will post a solution to this problem tomorrow, and then discuss what happens if the determinant is negative. Feel free to post your own solutions in the comments.

 

If you liked this article, please share it with your Facebook friends:

The Discriminant of a Quadratic Equation
Part 1

Recall that the quadratic equation ax² + bx + c = 0 can be solved using the quadratic formula:

For more information on the quadratic formula, see the following posts:

Quadratic Formula – Part 1   Quadratic Formula – Part 2

Before we go on, you may also want to review the information on square roots that can be found here:

Square Root Basics

The discriminant of the quadratic equation ax² + bx + c = 0 is the quantity Δ defined by

Δ = b² – 4ac

In other words, the discriminant is simply the expression that appears under the square root in the quadratic formula.

Although computing the discriminant of a quadratic equation does not give the roots (solutions) of the equation, it does give us a lot of information about the nature of the roots and the graph of the equation.

For example, if the discriminant of the quadratic equation ax² + bx + c = 0 is 0, then the quadratic formula simplifies to

x = –b/2a,

and we see that there is just one solution.

If the coefficients a and b are integers, then the unique solution will be a rational number.

Graphically, this means that the graph of the function y = ax² + bx + c is a parabola that intersects the x-axis at one point.

An example is given by the red parabola in the image above.

Note: The discriminant does not tell us if the parabola opens upwards or downwards. However, this is easy to determine simply by looking at the value of a.

If a > 0 (i.e. a is a positive number), then the parabola opens upwards.

If a < 0 (i.e. a is a negative number), then the parabola opens downwards.

So, the red parabola in the image above has an equation of the form y = ax² + bx + c where a < 0 and Δ = 0

Example: Find the discriminant of x² + 6x + 9 = 0. Then describe the nature of the roots of the equation, and describe the graph of the function y = x² + 6x + 9.

I will post a solution to this problem tomorrow, and then discuss other possibilities for the determinant. Feel free to post your own solutions in the comments.

 

If you liked this article, please share it with your Facebook friends:

Square Root Basics

A number a is a square root of a number x if a² = x (or equivalently, a ⋅ a = x).

Example: 3 is a square root of 9 because 3² = 3 ⋅ 3 = 9.

–3 is also a square root of 9 because (–3)² = (–3)(–3) = 9.

We see that 9 has two square roots: 3 and –3. We sometimes combine these two and say that the two square roots of 9 are ±3.

Square Root Symbol

Students sometimes get confused when using the square root symbol:

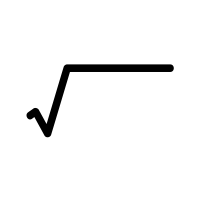
The symbol above represents the positive square root. So, for example, we have

So even though 9 has the two square roots ±3, when we put 9 under the symbol, the result is just 3 (and not –3). You may want to compare this with the Square Root Property (students often get the square root property confused with taking the positive square root of a number).

If we want the negative square root of a number, we need to place a minus sign before the square root symbol.

And if we want both square roots of a number, we should place the symbol ± before the square root symbol.

“Types” of Square Roots

All numbers, with the exception of 0, have two square roots. The number 0 has just one square root because both the positive and negative square root of 0 are both 0.

When taking positive and negative square roots of numbers, it’s worth trying to determine the “type” of number that you get. For example, whenever we take the square root of a nonzero integer (the set of integers is {…–3, –2, –1, 0, 1, 2, 3,…}), the result can be an integer, an irrational number, or a pure imaginary number (see this: Complex Numbers). When we identify the type of roots of a number we usually refer to this as determining the nature of the roots.

Examples: Determine the nature of the roots of 16, 11, –2, and 0.

Solution: Since 16 is a positive perfect square, the two square roots of 16 are integers (in fact, they are 4 and –4).

Since 11 is positive, but not a perfect square, the two square roots of 11 are irrational numbers.

Since –2 is negative, the two square roots of –2 are pure imaginary numbers.

Finally, 0 has just one square root…itself. In particular, 0 has one square root, which is an integer.

Note: If a positive integer is not a perfect square, then it’s square root will always be irrational. The proof of this result is beyond the scope of this article. I will discuss this further in a future post. 

 

If you liked this article, please share it with your Facebook friends:

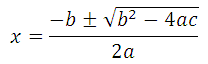Derivation of the Quadratic Formula

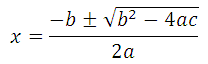
Last week we went over how to solve quadratic equations using the quadratic formula. You can see those posts here: Quadratic Formula 1   2

Recall that the solutions to the quadratic equation ax² + bx + c = 0 are

At the end of the second post, I posed the following problem:

Challenge Problem: Solve the general quadratic equation ax² + bx + c = 0 by completing the square, and note that this gives a derivation of the quadratic formula.

I will now provide a detailed solution. You may want to review the following posts before reading the following solution:

Square Root Property     Completing the Square     Solving Quadratic Equations

Solution:

 

The derivation above was challenging. Try to understand each step. If you have any question on a particular step, feel free to post your question in the comments.

If you liked this article, please share it with your Facebook friends:

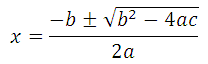The Quadratic Formula
Part 2

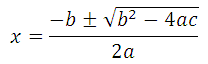
Yesterday we began discussing the quadratic formula, and I asked you to solve a specific quadratic equation using the formula. You can see that post here: Solving Quadratic Equations with the Quadratic Formula

Today I will provide the solution to that problem. For your reference, let me give you the quadratic formula one more time:

The solutions to the quadratic equation ax² + bx + c = 0 are

Example: Solve the quadratic equation x² – 2x – 15 = 0 by using the quadratic formula.

Solution:

So, the two solutions are 1 + 4 = 5, and 1 – 4 = –3

Note: This particular problem could be solved more easily by factoring. 

Why does the quadratic formula look so messy? It’s not a very pleasant looking formula. It would have been nicer if we had a simpler formula for solving a quadratic equation. But unfortunately, this is simply what it turned out to be. As a challenging exercise, I would like you to see this for yourself firsthand. I will give a full solution tomorrow:

Challenge Problem: Solve the general quadratic equation ax² + bx + c = 0 by completing the square, and note that this gives a derivation of the quadratic formula.

If you liked this article, please share it with your Facebook friends:

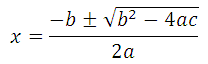Solving Quadratic Equations
with the Quadratic Formula

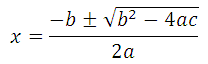
A quadratic equation has the form ax² + bx + c = 0.

The quadratic formula is a formula that gives us all solutions to a quadratic equation right away. The formula is as follows:

Example: Solve the quadratic equation x² – 2x – 15 = 0 by using the quadratic formula.

We have previously solved this problem by completing the square. You can see that solution here: Solution by Completing the Square

Try to solve this problem by using the quadratic formula. I will give the full solution tomorrow.

 

If you liked this article, please share it with your Facebook friends: