500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

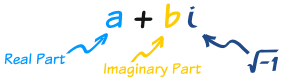
Complex Numbers
Solution to Division Problem

Several days ago I began writing a series of posts about complex numbers. You can see that post here: Complex Numbers  Addition and Subtraction  Multiplication  Division

Today I would like to provide a solution to Thursday’s division problem. Here is the problem one more time, followed by a solution:

Example:

Solution: 

 

 

For those of you that prefer videos…

 

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

Speak to you soon!

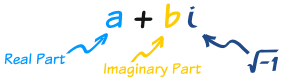
Complex Numbers
Division

A few days ago I began talking about complex numbers, and we learned how to raise the complex number i to any power. You can see that post here: Complex Numbers – Examples and Powers of i

We then reviewed how to add, subtract, and multiply complex numbers, and I gave you a problem to try involving multiplication. You can see those posts here: Addition and Subtraction  Multiplication

Today I will go over how to divide complex numbers. But first I will provide a solution to yesterday’s multiplication problem. Here is the problem one more time, followed by a solution:

Example: Compute (2 – 3i)(–5 + 6i)

Solution: (2 – 3i)(–5 + 6i) = (–10 + 18) + (12 + 15)i = 8 + 27i

 

Division

The conjugate of the complex number a + bi is the complex number a – bi.

Examples:

The conjugate of –5 + 6i is –5 – 6i.

The conjugate of 3 – 2i is 3 + 2i.

Note that when we multiply conjugates together we always get a real number. In fact, we have

(a + bi)(a – bi) = a² + b²

We can put the quotient of two complex numbers into standard form by multiplying both the numerator and denominator by the conjugate of the denominator. This is best understood with an example.

Example:

Hint: Multiply both the numerator and denominator of the fraction by the conjugate of the denominator. The denominator will them become a real number, and the resulting fraction can then be written in the form a + bi. 

I will provide a solution to this question tomorrow. Meanwhile, please post your attempted solutions in the comments below.

For those of you that prefer videos…

 

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

Speak to you soon!

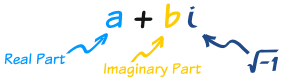
Complex Numbers
Multiplication

A couple of days ago I introduced complex numbers, and we learned how to raise the complex number i to any power. You can see that post here: Complex Numbers – Examples and Powers of i

Yesterday we reviewed how to add and subtract complex numbers, and I gave you a problem to try involving subtraction. You can see that post here: Complex Numbers – Addition and Subtraction

Today I will go over how to multiply complex numbers. But first I will provide a solution to yesterday’s problem. Here is the problem one more time, followed by a solution:

Example: When we subtract 2 – 3i from –5 + 6i we get what complex number?

Solution: (–5 + 6i) – (2 – 3i) = –5 + 6i – 2 + 3i = –7 + 9i.

 

 

Multiplication

We can multiply two complex numbers by formally taking the product of two binomials and then replacing i²  by –1. That process leads to the following formula:

(a + bi)(c + di) = (ac – bd) + (ad + bc)i

Example: Compute (2 – 3i)(–5 + 6i)

I will provide a solution to this question tomorrow. Meanwhile, please post your attempted solutions in the comments below.

For those of you that prefer videos…

 

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

Speak to you soon!

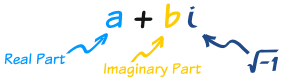
Complex Numbers
Addition and Subtraction

Yesterday we began discussing complex numbers, and I gave you a problem to try involving raising i to a power. You can see that post here: Complex Numbers – Examples and Powers of i

Today I will go over how to add and subtract complex numbers. But first I will provide a solution to yesterday’s problem. Here is the problem one more time, followed by a solution:

 

Example: Compute i⁵³.

Solution: When we divide 53 be 4 we get a remainder of 1. So i⁵³ = i¹ = i.

Notes: (1) For a review of how to compute remainders, see the following post: Remainders

(2) This computation can also be done quickly in your calculator, but be careful. Your calculator may sometimes “disguise” the number 0 with a tiny number in scientific notation. For example, when we type  i^ 53 ENTER into out TI-84, we get an output of –3E–13 + i. The expression –3E–13 represents a tiny number in scientific notation which is essentially 0. So this should be read as 0 + i = i.

 

Addition and Subtraction

We add two complex numbers simply by adding their real parts, and then adding their imaginary parts.

(a + bi) + (c + di) = (a + c) + (b + d)i

Example: The sum of the complex numbers 2 – 3i and –5 + 6i is:

(2 – 3i) + (–5 + 6i) = (2 – 5) + (–3 + 6)i = –3 + 3i

Subtraction is similar.

(a + bi) – (c + di) = (a – c) + (b – d)i

Example 5: When we subtract 2 – 3i from –5 + 6i we get what complex number?

I will provide a solution to this question tomorrow. Meanwhile, please post your attempted solutions in the comments below.

For those of you that prefer videos…

 

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

Speak to you soon!

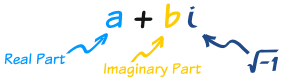
Complex Numbers

A complex number can be written in the form a + bi where a and b are real numbers and i² = –1.

Examples: The following are examples of complex numbers.

2 + 3i

3/2 + (–2i) = 3/2 – 2i

 –π + 2.6i

0 + 5i = 5i                    This is called a pure imaginary number.

17 + 0i = 17                 This is called a real number.

0 + 0i = 0                     This is zero.

Powers of i

By definition, when we raise any number to the 0 power, we get 1. So in particular, we have i⁰ = 1.

Similarly, when we raise any number to the power of 1, we just get that number. So i¹ = i.

By the definition of i, we have i² = –1.

i³ = (i²)(i) = (–1)i = –i.

i⁴ = (i²)(i²) = (–1)(–1) = 1.

i⁵ = (i⁴)(i) = (1)(i) = i.

⋯

Notice that the pattern begins to repeat.

Starting with i⁰ = 1, we have

i⁰ = 1               i¹ = i              i² = –1             i³ = –i

i⁴ = 1               i⁵ = i              i⁶ = –1             i⁷ = –i

i⁸ = 1               i⁹ = i              i¹⁰ = –1             i¹¹ = –i

⋯

In other words, when we raise i to a nonnegative integer, there are only four possible answers:

1, i, –1, or –i

To decide which of these values is correct, we can find the remainder upon dividing the exponent by 4.

Example: Compute i⁵³.

I will provide a solution to this question tomorrow. Meanwhile, please post your attempted solutions in the comments below.

For those of you that prefer videos…

 

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

Speak to you soon!

28 SAT Math Lessons – Beginner – Half Price

I’ve just updated the cover of the third book in my 28 SAT Math Lessons series. The book is currently available on Amazon for half of the regular price. Click the following link to get to the book’s Amazon page:

28 SAT MATH LESSONS – BEGINNER

Inverse Variation Question 4 with Solution

Last week, I went over inverse variation, and I gave you four inverse variation problems to try on your own. You can see that post here: Inverse Variation

Today I would like to give a solution to the last of those four problems. You can see a solution to the first three problems here: Q1  Q2  Q3

Example: Suppose that z varies directly as x² and inversely as y³. If z = 9 when x = 3 and y = 2, what is y when z = 4.5 and x = 6 ?

Try to solve the problem yourself before checking the solution below.

Solution: We are given that z =  kx²/y³   for some constant k. Since z = 9 when x = 3 and y = 2, we have 9 =  k(3)²/2³   =  9k/8. So k = 8, and z =  8x²/y³ . We now substitute z = 4.5 and x = 6 to get 4.5 =  8(6)²/y³ . So y³ =  8(36)/4.5  = 64, and therefore y = 4, choice D.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Inverse Variation Question 3 with Solution

Last week, I went over inverse variation, and I gave you four inverse variation problems to try on your own. You can see that post here: Inverse Variation

Today I would like to give a solution to the third of those four problems. You can see a solution to the first two problems here: Q1  Q2

Example: If x ≠ 0 and x is directly proportional to y, which of the following is inversely proportional to  1/y² ?

A) x²
B) x
C) 1/x
D) 1/x²

Try to solve the problem yourself before checking the solution below.

Solution: Since x is directly proportional to y, x = ky for some constant k.

Taking the reciprocal of each side of this equation gives us 1/x = 1/ky.

Cross multiplying yields ky = x. 

So k = x(1/y). Squaring each side of this last equation gives k² = x²(1/y²).

Since k² is a constant, x² is inversely proportional to 1/y². So the answer is choice A.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends: