500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Inverse Variation Question 2 with Solution

Last week, I went over inverse variation, and I gave you four inverse variation problems to try on your own. You can see that post here: Inverse Variation

Today I would like to give a solution to the second of those four problems. You can see a solution to the first problem here: Inverse Variation Q1

Example: If x varies inversely as y², and x is 3 when y is 5, then what is x when y is 3 ?

Try to solve the problem yourself before checking the solution below.

Solution: We are given that y = 5 when x = 3. Since  x varies inversely as y², we have that xy² is a constant. So we get the following equation: (3)(25) = x(9). So 75 = 9x, and therefore x = 75/9 = 25/3.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Inverse Variation Question 1 with Solutions

Last week, I went over inverse variation, and I gave you four inverse variation problems to try on your own. You can see that post here: Inverse Variation

Today I would like to give a solution to the first of those four problems. I will give solutions to the other three problems throughout this week.

Example: If y = k/x and y = 9 when x = 14, then what is y when x = 6 ?

Try to solve the problem yourself before checking the solutions below.

Solutions: 

(1) We are given that y = 9 when x = 14, so that 9 = k/14, or k = 126. Thus, y = 126/x. When x = 6, we have y = 126/6 = 21.

(2) Since y varies directly as x,  xy  is a constant. So, we get the following equation:  (14)(9) = 6y. So, 126 = 6y, and y = 126/6 = 21.

(3) (14)(9)/6 = 21.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Inverse Variation

Last week, I gave you several posts on direct variation. You can see those posts by clicking the following links: Direct Variation  Q1  Q2  Q3

Today I would like to talk about inverse variation.

The following are all equivalent ways of saying the same thing:

(1) y varies inversely as x. 
(2) y is inversely proportional to x.
(3) y = k/x for some constant k.
(4)  xy  is constant.

The following is a consequence of (1), (2), (3), or (4)

(5) the graph of y = f(x) is a hyperbola

Note: (5) is not equivalent to (1), (2), (3), or (4).

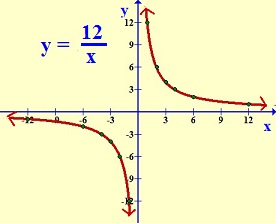
Example: In the equation y = 12/x, y varies inversely as x. Here is a partial table of values for this equation.

Note that we can tell that this table represents an inverse relationship between x and y because (1)(12) = (2)(6) = (3)(4) = (4)(3) = 12. Here the constant of variation is 12.

Here is a graph of the equation. On the left, you can see the full graph. On the right, we have a close-up in the first quadrant.

The various equivalent definitions of direct variation lead to several different ways to solve problems.

Example: If y = k/x and y = 8 when x = 3, then what is y when x = 6 ?

Try to solve the problem yourself before checking the solutions below.

Solutions: 

(1) We are given that y = 8 when x = 3, so that 8 = k/3, or k = 24. Thus, y = 24/x. When x = 6, we have y = 24/6 = 4.

(2) Since y varies directly as x,  xy  is a constant. So, we get the following equation:  (3)(8) = 6y. So, 24 = 6y, and y = 24/6 = 4.

(3) (8)(3)/6 = 4.

 

Here are a few more problems for you to try. I will provide solutions to these over the next few days.

1. If y = k/x and y = 9 when x = 14, then what is y when x = 6?

2. If x varies inversely as y², and x is 3 when y is 5, then what is x when y is 3

3. If x ≠ 0 and x is directly proportional to y, which of the following is inversely proportional to  1/y² ?

A) x²
B) x
C) 1/x
D) 1/x²

4. Suppose that z varies directly as x² and inversely as y³. If z = 9 when x = 3 and y = 2, what is y when z = 4.5 and x = 6 ?

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Direct Variation Question 3 with Solutions

Last week, I went over direct variation, and I gave you three direct variation problems to try on your own. You can see that post here: Direct Variation

Today I would like to give a solution to the last of those three problems. You can see solutions to the first two problems here: Q1  Q2

Example: If y is directly proportional to x, which of the following could express y in terms of x ?

A) 7x
B) x⁷
C) x + 7
D) 7/x

Try to solve the problem yourself before checking the solutions below.

Solution: Since  is directly proportional to , we have that  is a constant times . The only answer choice that satisfies this requirement is choice A.

 

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Direct Variation Question 2 with Solutions

Last week, I went over direct variation, and I gave you three direct variation problems to try on your own. You can see that post here: Direct Variation

Today I would like to give a solution to the second of those three problems. You can see solutions to the first problem here: Direct Variation Q1.

Example: The amount of revenue that an online magazine retailer makes in a month is directly proportional to the number of active subscribers to the magazine. In July, the magazine had a total of 1200 subscribers, and the retailer reported revenue of $7200. In August, the online magazine had a total of 1500 subscribers. How much revenue did the retailer make?

Try to solve the problem yourself before checking the solutions below.

Solutions: 

(1) Since the revenue, R, is directly proportional to the number of subscribers, x, R = kx for some constant k. We are given that R = 7200 when x = 1200, so that 7200 = k(1200), or k = 7200/1200 = 6. Thus, y = 6x. When x = 1500, we have y = 6 ⋅ 1500 = 9000.

(2) Since R is directly proportional to x,  R/x  is a constant. So we get the following ratio:  7200/1200 = R/1500. Cross multiplying gives 1200R = 7200 ⋅ 1500, or equivalently, R = (7200⋅1500)/1200 = 9000.

(3) The graph of R = f(x) is a line passing through the points (0, 0) and (1200, 7200). The slope of this line is  (7200 – 0)/(1200 – 0) = 6. Writing the equation of the line in slope-intercept form we have y = 6x. As in solution 1, when x = 1500, we have y = 6 ⋅ 1500 = 9000.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Direct Variation Question 1 with Solutions

Yesterday, I went over direct variation, and I gave you three direct variation problems to try on your own. You can see that post here: Direct Variation

Today I would like to give a solution to the first of those three problems. I will give solutions to the other two problems throughout this week.

Example: If y = kx and y = 7 when x = 11, then what is y when x = 33?

Try to solve the problem yourself before checking the solutions below.

Solutions: 

(1) We are given that y = 7 when x = 11, so that 7 = k(11), or k = 7/11. Therefore y = 7x/11. When x = 33, we have y = 7(33)/11 = 21.

(2) Since y varies directly as x,  y/x  is a constant. So, we get the following ratio:  7/11 = y/33. Cross multiplying gives 231 = 11y, so that y = 21.

(3) The graph of y = f(x) is a line passing through the points (0,0) and (11, 7) The slope of this line is  (7 – 0)/(11 – 0) = 7/11. Writing the equation of the line in slope-intercept form we have y = 7/11 x. As in solution 1, when x = 33, we have y = 7(33)/11 = 21.

(4) To get from x = 11 to x = 33 we multiply x by 3. So we have to also multiply y by 3. We get 3(7) = 21.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Direct Variation

Today I would like to talk about direct variation – a topic that shows up on standardized tests such as the ACT, SAT, and GRE.

The following are all equivalent ways of saying the same thing:

(1) y varies directly as x. 
(2) y is directly proportional to x.
(3) y = kx for some constant k.
(4)  y/x  is constant.
(5) the graph of y = f(x) is a nonvertical line through the origin.

Example: In the equation y = 5x, y varies directly as x. Here is a partial table of values for this equation.

Note that we can tell that this table represents a direct relationship between x and y because  5/1 = 10/2 = 15/3 = 20/4. Here the constant of variation is 5.

Here is a graph of the equation.

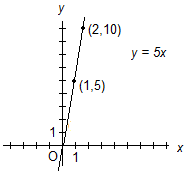
Note that we can tell that this graph represents a direct relationship between x and y because it is a nonvertical line through the origin. The constant of variation is the slope of the line, in this case m = 5.

The various equivalent definitions of direct variation lead to several different ways to solve problems.

Example: If y = kx and y = 5 when x = 8, then what is y when x = 24 ?

Try to solve the problem yourself before checking the solutions below.

Solutions: 

(1) We are given that y = 5 when x = 8, so that 5 = k(8), or k = 5/8. Therefore y = 5x/8. When x = 24, we have y = 5(24)/8 = 15.

(2) Since y varies directly as x,  y/x  is a constant. So, we get the following ratio:  5/8 = y/24. Cross multiplying gives 120 = 8y, so that y = 15.

(3) The graph of y = f(x) is a line passing through the points (0,0) and (8,5) The slope of this line is  (5 – 0)/(8 – 0) = 5/8. Writing the equation of the line in slope-intercept form we have y = 5/8 x. As in solution 1, when x = 24, we have y = 5(24)/8 = 15.

(4) To get from x = 8 to x = 24 we multiply x by 3. So we have to also multiply y by 3. We get 3(5) = 15.

 

Here are a few more problems for you to try. I will provide solutions to these over the next few days.

1. If y = kx and y = 7 when x = 11, then what is y when x = 33?

2. The amount of revenue that an online magazine retailer makes in a month is directly proportional to the number of active subscribers to the magazine. In July, the magazine had a total of 1200 subscribers, and the retailer reported revenue of $7200. In August, the online magazine had a total of 1500 subscribers. How much revenue did the retailer make?

3. If y is directly proportional to x, which of the following could express y in terms of x ?

A) 7x
B) x⁷
C) x + 7
D) 7/x

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends: