
500 New SAT Math Problems
Just 19.99 on Amazon
Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.
The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.
The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems
If you have any questions, feel free to contact me at steve@SATPrepGet800.com
Thank you all for your continued support!
A Trick For Free Two Day Shipping
I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.
Sign Up For Amazon Prime For Free
If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.
This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.
After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.
Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.
Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:
Sign Up For Amazon Prime For Free
If you think your friends might be interested in this special offer, please share it with them on Facebook:
Thank you all for your continued support!
 SAT Chemistry Problem with Solution –
SAT Chemistry Problem with Solution –
Product and Reactant Relationships

Today I would like to give a solution to yesterday’s SAT Chemistry problem. You can see the original question here: SAT Chemistry Problem – Product and Reactant Relationships
This problem is from the book 320 SAT Chemistry Problems arranged by Topic and Difficulty Level. Here is the problem one more time, followed by the solution.
Level 4 Product and Reactant Relationships
How many moles of water can be produced by the reaction of 4 moles of hydrogen gas with 4 moles of oxygen gas?
A) 2
B) 4
C) 8
D) 10
E) 16
*Solution: According to the stoichiometry, hydrogen is the limiting reactant. Only 2 moles of water will be produced, choice A.
Remarks: (1) The first step for this problem is to write out the chemicals involved and create a balanced equation. This will allow us to determine the relationship between the reactants. It is important to know the coefficients of the reaction because it is very likely that one reactant will be the limiting reagent or limiting reactant. The unbalanced equation will be H2 + O2 → H2O. For a review of balancing equations, see problem 12 in 320 SAT Chemistry Problems. The balanced reaction ends up being 2H2 + O2 → 2H2O.
(2) Even though there is an equal amount of moles of hydrogen and oxygen given, the hydrogen will run out first. This is because the reaction uses twice as much hydrogen as oxygen. We can compare limiting reagent problems to building sandwiches. In this hypothetical, we will say that a sandwich is two slices of bread and three slices of cheese. The stoichiometry would be 2 Bread + 3 Cheese → 1 sandwich.
If you were given 10 slices of bread and 10 slices of cheese and told to make as many sandwiches as possible, you would see that the cheese runs out first. We can define this mathematically by dividing the total amount of each sandwich ‘reactant’ by its coefficient. Looking at the bread ‘reactant’, we get (10 slices of bread)/(2 slices per sandwich) = 5 sandwiches. Looking at the cheese ‘reactant’, we get (10 slices of cheese)/(3 slices per sandwich) = 3 . 3 sandwiches. We would run out of cheese and have leftover bread. This is what it means for a reactant to be limiting. It prevents the use of the other reactant because it runs out.
More Test Prep Books from Get 800
Check out the other SAT subject test books from the Get 800 collection here: Get 800 SAT Subject Test Books
Thank you all for your continued support!
 SAT Chemistry Problem –
SAT Chemistry Problem –
Product and Reactant Relationships

Today I would like to give you an SAT Chemistry problem from the book 320 SAT Chemistry Problems arranged by Topic and Difficulty Level. I will post a full solution tomorrow.
Level 4 Product and Reactant Relationships
How many moles of water can be produced by the reaction of 4 moles of hydrogen gas with 4 moles of oxygen gas?
A) 2
B) 4
C) 8
D) 10
E) 16
More Test Prep Books from Get 800
Check out the other SAT subject test books from the Get 800 collection here: Get 800 SAT Subject Test Books
If you think your friends might be interested in this article, please share it with them on Facebook:
Thank you all for your continued support!
 Draw Your Own Figure
Draw Your Own Figure
Question 4 with Solution

Last week, I went over a strategy for solving certain math problems on standardized tests by drawing a figure, and I gave you four problems to try on your own. You can see that post here: Math Strategy: Draw Your Own Figure
Today I would like to give a solution to the last of those four problems. You can see solutions for the first three problems here: Draw Your Own Figure: Q1 Q2 Q3.
Example: In rectangle PQRS, point T is the midpoint of side PQ. If the area of quadrilateral QRST is 0.8, what is the area of rectangle PQRS ?
Try to solve the problem yourself before checking the solution below.
Solution: Let’s begin by drawing a picture.
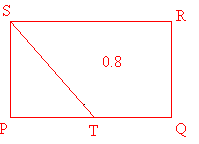
This picture alone really sheds some light on the situation. Lets now chop up our picture into 4 equal parts.
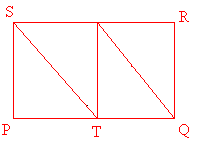
To get the area of one of those pieces simply divide 0.8 by 3. In our calculator we get
.266666666666667 or 4/15 if we change back to a fraction.
This is 1/4 of the area of the rectangle, so we simply multiply this result by 4 to get the answer 16/15.
More Problems with Explanations
If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
 Draw Your Own Figure
Draw Your Own Figure
Question 3 with Solution

Last week, I went over a strategy for solving certain math problems on standardized tests by drawing a figure, and I gave you four problems to try on your own. You can see that post here: Math Strategy: Draw Your Own Figure
Today I would like to give a solution to the third of those four problems. You can see solutions for the first two problems here: Draw Your Own Figure: Q1 Q2.
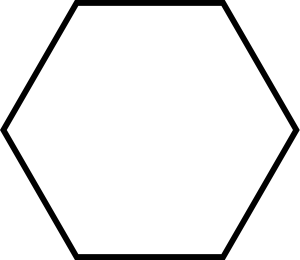
Example: Point A is a vertex of a 6-sided polygon. The polygon has 6 sides of equal length and 6 angles of equal measure. When all possible diagonals are drawn from point A in the polygon, how many triangles are formed?
Try to solve the problem yourself before checking the solution below.
Solution: We draw a picture.
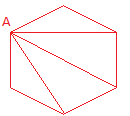
Observe that the number of triangles is 4.
More Problems with Explanations
If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
 Draw Your Own Figure
Draw Your Own Figure
Question 2 with Solution

Last week, I went over a strategy for solving certain math problems on standardized tests by drawing a figure, and I gave you four problems to try on your own. You can see that post here: Math Strategy: Draw Your Own Figure
Today I would like to give a solution to the second of those four problems. You can see a solution for the first problem here: Draw Your Own Figure: Question 1.
Example: If line m is perpendicular to segment PQ at point R, and PR = RQ, how many points on line m are equidistant from point P and point Q ?
A) One
B) Two
C) Three
D) More than three
Try to solve the problem yourself before checking the solution below.
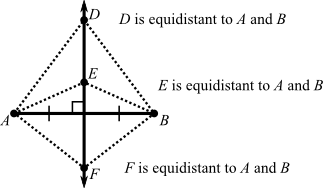
Solution: Recall first that equidistant means at the same distance. So we’re looking for points on line m that are at the same distance from P as they are from Q. Let’s begin by drawing a picture:
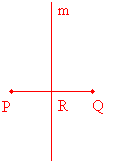
Notice that R is equidistant from P and Q, so there is at least one. Let’s draw some more.
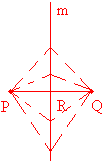
Since there are 5 shown in the above picture, the answer is choice D.
Note: Every point on line m is actually equidistant from P and Q. m is the perpendicular bisector of line segment PQ.
The perpendicular bisector of a line segment is a line perpendicular to the segment that passes through the midpoint of the segment.
More Problems with Explanations
If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
 Draw Your Own Figure
Draw Your Own Figure
Question 1 with Solution

Last week, I went over a strategy for solving certain math problems on standardized tests by drawing a figure, and I gave you four problems to try on your own. You can see that post here: Math Strategy: Draw Your Own Figure
Today I would like to give a solution to the first of those four problems. I will give solutions to the other three problems throughout this week.
Example: What is the area of a right triangle whose sides have lengths 14, 48, and 50?
Try to solve the problem yourself before checking the solution below.
Solution: Let’s begin by drawing a picture
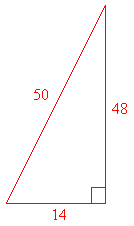
Remember: The hypotenuse of a right triangle (the side opposite the right angle) is always longer than both legs.
In a right triangle we can always take the two legs to be the base and the height (in either order). So b = 14, h = 48, and
A = 1/2 bh = 1/2(14)(48) = 336.
More Problems with Explanations
If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
 Draw Your Own Figure
Draw Your Own Figure

Today I would like to remind you of a very simple but effective strategy for solving math problems on standardized tests such as the ACT, SAT, and GRE.
If a math problem does not have a figure above it, then do not hesitate to draw your own. Sometimes drawing a quick picture of a situation makes a problem very easy, or at least easier. This is especially helpful with geometry problems.
Example: Segment PQ has midpoint M. If the length of PM is t, what is the length of PQ in terms of t ?
Try to solve the problem yourself before checking the solution below.
Solution: Let’s begin by drawing a picture
![]()
From the picture, we see that PQ has twice the length of PM. Thus, the length of PQ is 2t.
Here are a few more problems for you to try. Try to draw a picture. I will provide solutions to these over the next few days.
1. What is the area of a right triangle whose sides have lengths 14, 48, and 50?
2. If line m is perpendicular to segment PQ at point R, and PR = RQ, how many points on line m are equidistant from point P and point Q ?
A) One
B) Two
C) Three
D) More than three
3. Point A is a vertex of a 6-sided polygon. The polygon has 6 sides of equal length and 6 angles of equal measure. When all possible diagonals are drawn from point A in the polygon, how many triangles are formed?
4. In rectangle PQRS, point T is the midpoint of side PQ. If the area of quadrilateral QRST is 0.8, what is the area of rectangle PQRS ?
More Problems with Explanations
If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:


