500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hard GRE Math Arithmetic Problems

Hello everybody. I think it’s time for all of you to do a little more work. Here are three challenging Level 5 GRE arithmetic questions. Note that all three of these questions are free response questions (or grid-ins). Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve each of these problems. I will post full solutions tomorrow.

Level 5 GRE Arithmetic Problems

1. If n is a positive integer such that the units (ones) digit of n² + 4n is 7 and the units digit of n  is not 7, what is the units digit of n + 3?

2. The sum of the positive odd integers less than 200 is subtracted from the sum of the positive even integers less than or equal to 200. What is the resulting difference?

3. The positive number k is the product of four different positive prime numbers. If the sum of these four prime numbers is a prime number greater than 20, what is the least possible value for k?

More Hard GRE Math Practice Problems

For many more hard GRE math problems like these, each with several fully explained solutions, check out 320 GRE Math Problems arranged by Topic and Difficulty Level. 

And if you think your friends would like to try these problems, please share:

Talk soon!

Differences of Large Sums –

An Advanced Math Strategy

Today I would like to show you how to solve math problems where you are asked to find two large sums and then subtract them.

These problems always remind me of a little story about a young boy named Karl Gauss. The story actually directly relates to the strategy I will be discussing, so it’s worth taking this little detour.

The Boy Karl Gauss

In a math class, a teacher set her students to a task to keep them busy for a few minutes.

In an attempt to keep the class quiet, the teacher asked the students to take out a piece of paper and add up the integers from 1 to 100 by hand.

The teacher was hoping for the students to painstakingly write down 1, 2, 3, 4, 5 etc… to 100, and then add the numbers together to get an answer. The teacher knew that this problem would take some time to complete as she, herself, took several minutes to get the answer.

However, one of her students, Karl, handed the teacher a piece of paper with the correct answer almost immediately. In the top left corner of the sheet, he had neatly written 5,050.

Nothing else.

Surprised that the student had the correct answer so quickly, the teacher asked how he did it.

“Oh, this was really easy” said Karl, “1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, 4 + 97 = 101… and so on. I could see that there are 100 pairs of numbers that add up to 101. So I multiplied 101 by 100 to get 10,100. I then divided by 2 because I added each number twice. So I wrote down the answer 5,050.”

Let’s take one last look at Karl’s computation in an easy to read format as we will be using this format to solve math problems in just a moment.

      1  +  2 + 3 + …+ 100
100+99+98+ … +  1
101+101+101+…+ 101

101+101+101+…+101

= 100(101)

= 10,100

10,100/2 = 5050

We are going to simulate Karl Gauss’s method above to get the answer to some seemingly difficult math questions quickly and without making careless computational errors. Don’t worry – I will explain everything step by step.

This method is best understood with examples So let’s jump right in with some problems.

Example 1

If x denotes the sum of the integers from 10 to 70 inclusive, and y denotes the sum of the integers from 80 to 140 inclusive, what is the value of y – x?

First, we write out each sum formally and line them up with y above x.

  80 + 81 + 82 + … + 140
10 + 11 + 12 + … + 70

Next subtract term by term.

  80 + 81 + 82 + … + 140
10 + 11 + 12 + … + 70
70 + 70 + 70 + … + 70

Now notice that we’re adding 70 to itself

70 – 10 + 1 = 61

times (by the fence-post formula – see yesterday’s blog post).

This is the same as multiplying 70 by 61. So we get 

(70)(61) = 4270.

Example 2

Let x ♦ y be defined as the sum of all integers between x and y. For example, 1 ♦ 4 = 2+3=5. What is the value of

(60 ♦ 900) – (63 ♦ 898)?

As above, we write out each sum formally, line them up so that the numbers match up, and then subtract term by term.

     61 + 62 + 63 + 64 + … + 897 + 898 + 899
          64 + … + 897 
61 + 62 + 63 + 0 + …  … + 0 + 898 + 899

So the answer is

61 + 62 + + 63 + 898 + 899

= 1983.

Note that in each of the above problems, the numbers were lined up in different ways. It is usually pretty clear how to line up the numbers properly.

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

The Fence-Post Formula 

Today I want to  discuss a math concept that can be used to solve certain types of problems that appear every now and then on standardized tests. Tutors tend not to spend much time (if any) helping students prepare for this type of problem as it seldom appears. But if you want a perfect math score, then you want to be able to recognize all problem types and be able to answer them correctly (and quickly!).

This problem type involves what I like to call “Fence-Posting,” a technique that allows us to count the number of integers in a consecutive list.

Fence-post formula: The number of integers from a to b, inclusive, is

b – a + 1.

The word inclusive means that we include the extreme values.

For example, if we want to count the integers from 1 to 3, inclusive, we can easily see that there are 3 of them. Note that we do include the extreme values 1 and 3. Using the fence-post formula we get

3 – 1 + 1 = 3.

The most common error when attempting to count the integers in a list is to simply subtract the smallest value from the largest value (without adding 1). Note that in the previous example, this would give an incorrect answer of 2.

As another simple example, let’s count the number of integers from 5 to 12, inclusive, in two ways – directly and by fence-posting. First directly – the integers from 5 to 12 are 5, 6, 7, 8, 9, 10, 11, 12, and we see that there are 8 of them. Now using the fence-post formula we have

12 – 5 + 1 = 8.

Note that the computation 12 – 5 gives an incorrect answer of 7.

If you ever happen to forget this little formula test it out on a small list of numbers as I just did in the two examples above. But it’s nice to have this one committed to memory so that it is there for you when you need it.

Let’s take a look at a couple of examples where we can use fence-posting to obtain an answer efficiently.

Example 1

Set X contains only the integers 0 through 180 inclusive. If a number is selected at random from X, what is the probability that the number selected will be greater than the median of the numbers in X?

So first of all we need to find out how many integers there are in the set X. By the fence-post formula there are

180 – 0 + 1 = 181

integers in this set.

The median of the numbers in set X is 90 (note that in a set of consecutive integers the median is equal to the average of the first and last integer). Again, by the fence-post formula, we see that there are

180 – 91 + 1 = 90

integers greater than the median.

From this we see that the desired probability is

90/181 (approximately 0.4972375691).

So we grid in .497. (Note that this is a grid-in question because I have not provided answer choices).

Remember with grid in problems, we have only four slots available. We can simply truncate the final answer that we get in our calculator to fit in the four slots.

Example 2

How many numbers between 72 and 356 can be expressed as 5x + 3, where x is an integer?

This problem is more complicated than the first example, but we can use fence-posting to solve this one too: Let’s start by guessing x-values until we find the smallest and largest values of x satisfying

72 < 5x + 3 < 356.

Since we have 5(13) + 3 = 68 and also 5(14) + 3 = 73 we see that 14 is the smallest value of x satisfying the inequality.

Since 5(70) + 3 = 353 and 5(71) + 3 = 358, the largest value of x satisfying the inequality is 70. 

It follows by fence-posting that the answer is 70 – 14 + 1 = 57.

Note that we also used the strategy of taking a guess to solve this problem. I discussed this strategy in a previous blog post. You can find that information by clicking on the link.

Algebraic solution: 

72 < 5x + 3 < 356
69 < 5x < 353
69/5 < x < 353/5
13.8 < x < 70.6
14 ≤ x ≤ 70

We get the last inequality because x must be an integer. Notice that this last inequality is not strict. For those of you not familiar with this piece of math lingo, an inequality that is not strict means that it is ‘less than or equal to’ rather than just ‘less than’.

Finally, t follows by fence-posting that the answer is 70 – 14 + 1 = 57.

Tomorrow I will be showing a quick method for computing differences of large sums. You will also see how the fence-post formula can sometimes be useful in solving these types of problems. Click the following link to read this article: Differences of Large Sums

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

AP Calculus AB Mean Value Theorem

Problem with Solution

Today I will provide a solution for yesterday’s AP Calculus AB Mean Value Theorem Problem. Once again here is the question: 

Let f(x) = –3x² + x – 5. A value of c that satisfies the conclusion of the Mean Value Theorem for f on the interval [–2,2] is

(A) –2
(B) –1/2
(C) –1/6
(D) 0

Solution: f ‘ (x)= –6x + 1, so that f ‘ (c) = –6c + 1.

f(2) = -3(2)² + 2 – 5 = –3(4) – 3 = –12 – 3 = –15.

f(–2) = –3(–2)² – 2 – 5 = –3(4) – 7 = –12 – 7 = –19. 

We now solve the equation f ‘ (c) = (f(2) – f(–2)) / (2 – (–2))  to get

–6c + 1 = (–15 – (–19)) / (2 + 2) = (–15 + 19) / 4 = 4 / 4 = 1

So –6c = 1 – 1 = 0, and c=0, choice (D).

Notes: (1) The Mean Value Theorem says that if f is a function that is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there is a real number c with a < c < b such that f ‘ (c) = (f(b) – f(a)) / (b – a).

In this problem a = –2, b = 2, and f(x) = –3x² + x – 5.

(2) Note that the function f(x) = –3x² + x – 5 is a polynomial. It is therefore continuous and differentiable everywhere. In particular, it is continuous on [–2,2] and differentiable on (–2,2). Therefore by the Mean Value Theorem, there is a c between –2 and 2 such that

f ‘ (c) = (f(2) – f(–2)) / (2 – (–2)).

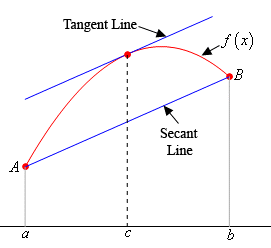
(3) Geometrically, f ‘ (c) is the slope of the tangent line to the graph of the function f at c, and (f(b) – f(a)) / (b – a)  is the slope of the secant line passing through the points A(a,f(a)), and B(b,f(b)).

The Mean Value Theorem says that the slopes of these two lines are the same. In other words, they are parallel.

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

AP Calculus AB – Mean Value Theorem

AP Calculus students tend to find problems involving the Mean Value Theorem very difficult. I often tell my students “If you don’t know what a problem is asking for, try using the Mean Value Theorem.”  This is due to the fact that most problems where the Mean Value Theorem is needed never actually mention the theorem in the problem itself.

Let’s try a very basic AP Calculus AB Mean Value Theorem problem (note that any Calculus AB problem can also appear on the BC exam). I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 2 Mean Value Theorem Problem

Let f(x) = –3x² + x – 5. A value of c that satisfies the conclusion of the Mean Value Theorem for f on the interval [–2,2] is

(A) –2
(B) –1/2
(C) –1/6
(D) 0

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

Hard Heart of Algebra Problem with Solutions

Yesterday I gave you a Level 5 “Heart of Algebra” problem for the SAT to try. Today I will provide a solution for this problem. If you have not yet attempted the problem go back and take a look at it first so you can try it on your own. Here is the link: Hard Heart of Algebra Problem for the SAT

Level 5 – Heart of Algebra

Here is the problem once again followed by several solutions:

3x – 7y = 12
kx + 21y = -35

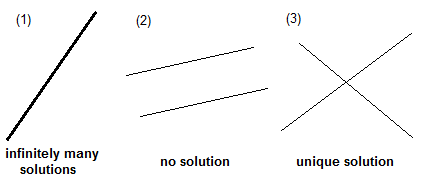
For which of the following values of k will the system of equations above have no solution?

(A)  9
(B)  3
(C) -3
(D) -9

Solution: The system of equations

ax + by = c
dx + ey = f

has no solution if a/d = b/e ≠ c/f. So we solve the equation 3/k = -7/21.  Cross multiplying yields 63 = -7k  so that k = 63/-7 = -9, choice (D).

Note: In this problem b/e ≠ c/f. Indeed, -7/21 ≠ 12/-35. This guarantees that the system of equations has no solution instead of infinitely many solutions.

* Quick solution: We multiply -7 by -3 to get 21. So we have k = (3)(-3) = -9, choice (D).

Note: The general form of an equation of a line is ax + by = c where a, b, and c are real numbers. More information about this type of equation can be found in New SAT Math Problems arranged by Topic and Difficulty Level.

Feel free to add your own solutions to the comments.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out the Get 800 collection of SAT math books. Click on the picture below for more information about these books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

Hard Heart of Algebra Problem for the SAT

Today I would like to provide an example of a hard “Heart of Algebra” problem that could show up on the revised SAT.

Level 5 – Heart of Algebra

3x – 7y = 12
kx + 21y = -35

For which of the following values of k will the system of equations above have no solution?

(A)  9
(B)  3
(C) -3
(D) -9

Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve the problem. I will post solutions to this problem next week.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out the Get 800 collection of SAT math books. Click on the picture below for more information about these books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

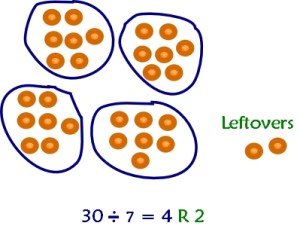
Hard Remainder Problem with Solution

Today I will provide a solution for the difficult remainder problem I asked you to attempt yesterday. Once again, you may want to read some of my older posts about remainders before going over the solution here.  You can find those posts by using the following links:

Can We Solve Remainder Problems Without Using Long Division?

The Cyclical Nature of Remainders

Remainders in Disguise

And now here is the question once more, followed by a complete solution.

Level 6 Remainder Problem

Find the remainder when 2¹²⁰ is divided by 3.

Solution by recognizing a pattern: 

2¹ = 2, remainder = 2
2² = 4, remainder = 1
2³ = 8, remainder = 2
2⁴ = 16, remainder = 1
2⁵ = 32, remainder = 2
2⁶ = 64, remainder = 1
2⁷ = 128, remainder = 2

Note that we evaluated the first 7 powers of 2, and then gave each of the remainders upon division by 3.

For example, 16 = 3(5) + 1, and so the remainder when 16 is divided by 3 is 1.

Now simply observe that all even powers of 2 give a remainder of 1 when divided by 3. Therefore, the answer is 1.

Remark: So how do we know with absolute certainty that the pattern we produced will continue indefinitely? After all, isn’t it possible that the pattern can stop at any time? Just because a pattern holds for the first 7 positive integers, it may not necessarily still hold for the 8th positive integer, or any other integer thereafter. But in this case it does.

Let’s prove two more general theorems that will imply that the pattern holds.

Theorem 1: If an integer gives a remainder of 1 when divided by 3, then twice that integer gives a reminder of 2 when divided by 3.

Proof: Let n be an integer that gives a remainder of 1 when divided by 3.

Then there is an integer k such that n = 3k + 1.

So 2n = 2(3k + 1) = 6k + 2 = 3(2k) + 2.

Since 2k is an integer, we have shown that 2n gives a remainder of 2 when divided by 3.

Theorem 2: If an integer gives a remainder of 2 when divided by 3, then twice that integer gives a reminder of 1 when divided by 3.

Proof: Let n be an integer that gives a remainder of 2 when divided by 3.

Then there is an integer k such that n = 3k + 2.

So 2n = 2(3k + 2) = 6k + 4 = 6k + 3 + 1 = 3(2k + 1) + 1.

Since 2k + 1 is an integer, we have shown that 2n gives a remainder of 1 when divided by 3.

After going through the proofs of these theorems, you should reflect back and make sure you understand why these two theorems imply that the pattern holds.

More Remainder Practice Problems

Don’t forget to take a look at the Get 800 collection of test prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

Hard Remainder Problem

Students are always asking me to solve some difficult problems. Today I would like to give you a difficult remainder problem similar to one a student recently asked me about. Before attempting this problem you may want to read some of my older posts on remainders. You can find them by using the following links:

Can We Solve Remainder Problems Without Using Long Division?

The Cyclical Nature of Remainders

Remainders in Disguise

And now here is a challenging problem for you to try. This problem is probably a little more difficult than any that would actually show up on a standardized test, but it’s always worth struggling with these harder problems a bit to help raise your level of mathematical maturity. Feel free to post your attempted solutions in the comments. I will provide a complete solution tomorrow.

Level 6 Remainder Problem

Find the remainder when 2¹²⁰ is divided by 3.

More Remainder Practice Problems

Don’t forget to take a look at the Get 800 collection of test prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

Solutions To Yesterday’s Hard Geometry Problems

Today I would like to post solutions to the three hard geometry questions I posted yesterday. If you still want further explanation after reading the below solutions please do not hesitate to ask.

Level 5 Geometry Problems

1. The lengths of the sides of a triangle are x, 16 and 31, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?

Solution: By the triangle rule, x lies between 31 – 16 = 15 and 31 + 16 = 47. That is, we have 15 < x < 47. But we are also given that x is the length of the shortest side of the triangle. So x < 16.Therefore we can grid in any number between 15 and 16. For example, we can grid in 15.1.

For more information on the triangle rule see the following article: The Triangle Rule

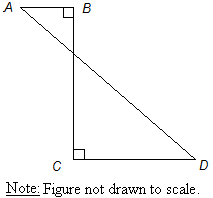
2. In the figure above, if AB = 4, BC = 24, and AD = 26, then CD =

Solution: The problem becomes much simpler if we “move” BC to the left and AB to the bottom as shown below.

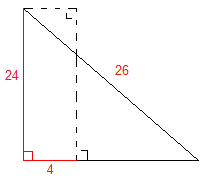
We now have a single right triangle and we can either use the Pythagorean Theorem, or better yet notice that 26 = (13)(2) and 24 = (12)(2). Thus the other leg of the triangle is (5)(2) = 10. So we see that CD must have length 10 – 4 = 6.

Remark: If we didn’t notice that this was a multiple of a 5-12-13 triangle, then we would use the Pythagorean Theorem as follows.

(x + 4)² + 24² = 26²
(x + 4)² + 576 = 676
(x + 4)² = 100
x + 4 = 10
x = 6

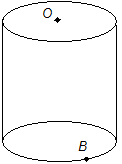
3. The figure above shows a right circular cylinder with diameter 6 and height 9. If point  O is the center of the top of the cylinder and B lies on the circumference of the bottom of the cylinder, what is the straight-line distance between  O and B?

Solution: We draw a right triangle inside the cylinder as follows:

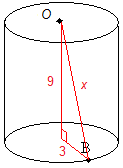
Note that the bottom leg of the triangle is equal to the radius of the circle (not the diameter) which is why it is 3 and not 6. We can now use the Pythagorean Theorem to find x.

x² = 3² + 9² = 9 + 81 = 90

Taking the square root gives x approximately equal to 9.4868. So we grid in 9.48 or 9.49.

More Geometry Practice Problems

For more hard geometry problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books.

If you think your friends would like to try these problems, please share:

Speak to you soon!