500 New SAT Math Problems – Just 19.99 Today Only

June 30, 2024

$500 New SAT Math Problems$

500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

~~The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.~~

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hard Geometry Problems

July 13, 2016

Hard Geometry Problems

I think it’s about time for all of you to do a little work. Here are three challenging Level 5 geometry questions. Problems like these can appear on the SAT, ACT or GRE (although on the ACT they would be multiple choice instead of free response). Note that all three of these questions are free response questions (or grid-ins). Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve each of these problems.

Level 5 Geometry Problems

The lengths of the sides of a triangle are x, 16 and 31, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?

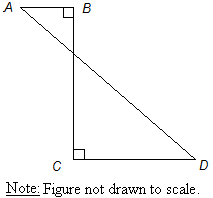
intersecting triangles

In the figure above, if AB = 4, BC = 24, and AD = 26, then CD =

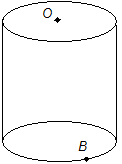
cylinder

The figure above shows a right circular cylinder with diameter 6 and height 9. If point O is the center of the top of the cylinder and B lies on the circumference of the bottom of the cylinder, what is the straight-line distance between O and B?

$320 SAT Math Problems$
320 SAT Math Problems – New Edition

Today I would like to announce my new math prep book for the new SAT: 320 SAT Math Problems arranged by Topic and Difficulty Level – Second Edition

This book will be released in about two weeks at a promotional price of about $5.50.

This sale may last for only a few hours, and once the sale ends the price will go up to $34.99. Amazon will automatically raise the price once a predetermined number of copies has been sold. If you want to take advantage of the sale price I strongly recommend that you get on the email notification list.

To be added to the notification list, simply send an email to steve@SATPrepGet800.com with “Notify me” written in the subject line.

In the meantime, you can take a look at my product page to see all of the other books from the Get 800 collection: Get 800 Product Page

If you think your friends might be interested in being notified of this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hard GRE Math Comparison Problem with Solution

July 11, 2016

Hard GRE Math Comparison Problem

with Solution

Yesterday I posted a Level 4 GRE math comparison problem. Click the following link to see that post: Hard GRE Math Comparison Problem

Some of you already figured out how to solve this one. Today I will provide a solution to the problem.

Level 4 Arithmetic Comparison Problem

p is a prime number greater than 2.

Quantity A: The number of distinct prime factors of 27p
Quantity B: The number of distinct prime factors of 49p

A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

* Solution by picking numbers: If we let p = 3, then 27p = 27 ⋅ 3 = 3⁴, and 49p = 49 ⋅ 3 = 3 ⋅ 7². So Quantity A is 1 and Quantity B is 2. Therefore, Quantity B is greater than Quantity A.

Now, if we let p = 7, then 27p = 27 ⋅ 7 = 3³ ⋅ 7, and 49p = 49 ⋅ 7 = 7³. So Quantity A is 2 and Quantity B is 1. Therefore, Quantity A is greater than Quantity B.

So the answer is D.

Notes: (1) The only prime factor of 27 is 3 (27 = 3³), and the only prime factor of 49 is 7 (49 = 7²). So it seems natural to try 3 and 7 for p.

(2) If we choose any number for p other than 3 or 7, then Quantities A and B will be the same (they will both be equal to 2). Try setting p = 5, for example. I leave the details to the reader.

Hard GRE Math Comparison Problem

Today I would like to give you a Level 4 GRE math comparison problem . Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve each of these problems. I will be giving a full solution to this problem tomorrow.

Level 4 Arithmetic Comparison Problem

p is a prime number greater than 2.

Quantity A: The number of distinct prime factors of 27p
Quantity B: The number of distinct prime factors of 49p

A. Quantity A is greater.
B. Quantity B is greater.
C. The two quantities are equal.
D. The relationship cannot be determined from the information given.

New SAT Verbal Prep Book

The New SAT Verbal Prep Book for Reading and Writing Mastery gives you the most effective tips, tricks and tactics from Get 800, a prep company of doctors dedicated to their students achieving their dream SAT scores.

Click the following link to get to the book’s Amazon page: New SAT Verbal Prep Book

If you would like to take a look at a free sample of this book, click the following link: New SAT Verbal Free Sample

Take a look at my product page to see all of my books: Get 800 Product Page

A Trick For Free Two Day Shipping

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Please share this information with your Facebook friends:

The Features You Should Learn How to Use On Your Graphing Calculator

July 7, 2016

General Graphing Calculator Advice for the SAT/ACT

I always recommend that you use a TI-84 or comparable graphing calculator for the SAT or ACT.
It is important that you are comfortable with your calculator on test day, so make sure that you are consistently practicing with the calculator you plan to use.
Make sure that your calculator has fresh batteries the day of the test. Nobody will supply a calculator for you if yours dies.
You may have to switch between DEGREE and RADIAN modes during the test. If you are using a TI-84 (or equivalent) calculator press the MODE button and scroll down to the third line when necessary to switch between modes.

Graphing Calculator Features You Should Know for the SAT/ACT

Below are the most important things you should practice on your graphing calculator.

(1) Practice entering complicated computations in a single step, and know when to insert parentheses. In general, there are 4 instances when you should use parentheses in your calculator. Around numerators of fractions Around denominators of fractions Around exponents Whenever you actually see parentheses in the expression

Around numerators of fractions
Around denominators of fractions
Around exponents
Whenever you actually see parentheses in the expression

Examples: We will substitute a 5 in for x in each of the following examples.

TI-84 Graphing Calculator Examples

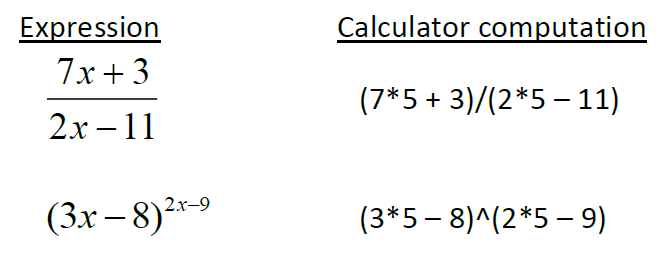
(2) Clear the screen before using it in a new problem. The big screen allows you to check over your computations easily.

(3) Press the ANS button (2^nd (-) ) to use your last answer in the next computation.

(4) Press 2^nd ENTER to bring up your last computation for editing. This is especially useful when you are plugging in answer choices, or guessing and checking.

(5) You can press 2^nd ENTER over and over again to cycle backwards through all the computations you have ever done.

(6) Know where the ,√ ,π and ^ buttons are so you can reach them quickly.

(7) Change a decimal to a fraction by pressing MATH ENTER ENTER.

(8) Press the MATH button – in the first menu that appears you can take cube roots and nth roots for any n.

(9) Know how to use the SIN, COS and TAN buttons as well as SIN^-1, COS^-1 and TAN^-1.

ACT only

The following features are necessary for the ACT only.

(10) Press the MATH button. Scroll right to NUM and you have lcm( and gcd(. Scroll right to PRB and you have nPr, nCr, and ! to compute permutations, combinations and factorials very quickly.

(11) Know where LOG button is so you can reach it quickly.

Advanced Features

The following items are less important but can be useful for both the SAT and ACT.

(12) Press the Y= button to enter a function, and then hit ZOOM 6 to graph it in a standard window.

(13) Practice using the WINDOW button to adjust the viewing window of your graph.

(14) Practice using the TRACE button to move along the graph and look at some of the points plotted.

(15) Pressing 2nd TRACE (which is really CALC) will bring up a menu of useful items. For example selecting ZERO will tell you where the graph hits the x-axis, or equivalently where the function is zero. Selecting MINIMUM or MAXIMUM can find the vertex of a parabola. Selecting INTERSECT will find the point of intersection of 2 graphs.

And now it’s time to start practicing lots of math problems. For this you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

See you tomorrow!

SAT Math Solutions – Part 2

July 6, 2016

SAT Math Solutions – Part 2

Two days ago I gave you two math problems for the revised SAT. To see that post click the following link:

SAT Math Problems for the Revised SAT

You can find a solution to the first problem here:

SAT Math Problems and Solutions for the Revised SAT

Today I will solve the second problem.

Level 2 Data Analysis

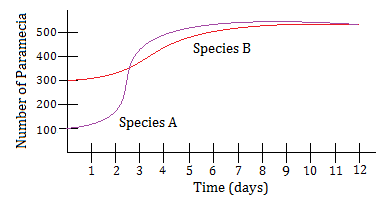
A puddle with an area of 500 cm², is monitored by scientists for the number of paramecia present. The scientists are interested in two distinct species, let’s call them “species A” and “species B.” At time t = 0, the scientists measure and estimate the amount of species A and species B present in the puddle. They then proceed to measure and record the number of each species of paramecium present every hour for 12 days. The data for each species, were then fit by a smooth curve, as shown in the graph above. Which of the following is a correct statement about the data above?

(A) At time t = 0, the number of species B present is 150% greater than the number of species A present.
(B) At time t = 0, the number of species A present is 75% less than the number of species B present.
(C) For the first 3 days, the average growth rate of species B is higher than the average growth rate of species A.
(D) The growth rate of both species A and species B decreases for the last 8 days.

Solution: The last 8 days correspond to times t = 4 through t = 12. During this time, the growth rate of both species is decreasing. So the answer is choice (D).

Notes: (1) 300 = 200 + 2(100), and therefore 300 is 200% greater than 100. This eliminates choice (A).

(2) We can also use the percent change formula

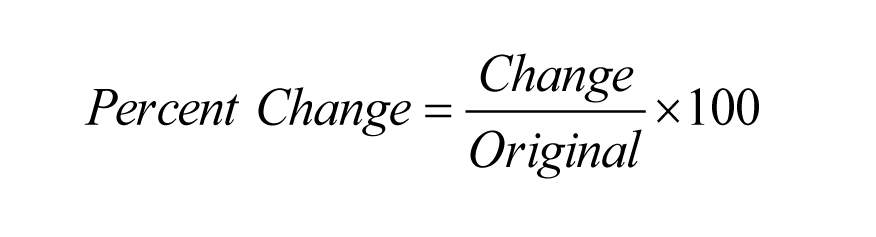
Here the original value is 100 and the change is 300 – 100 = 200. It follows that Percent Change = (200/100)*100 = 200%.

(3) To eliminate choice (B) we can use the percent change formula again with original value 300 and change 300 – 100 = 200:

.Percent Change = (200/300)*100 = 200/3 = 66 2/3%.

(4) We can compute the average growth rate over the interval from t = a to t = b, by computing the slope of the line passing through the points (a,f(a)) and (b,f(b)). That is, we would compute m =(f(b) – f(a))/(b – a).

For example, over the first 3 days, the average growth rate of species A is approximately (400 – 100)/(3 – 0) = 300/3 = 100 paramecia per day. The two points we used here were (0,100) and (3,400).

Similarly, over the first 3 days, the average growth rate of species B is approximately (350 – 300)/(3 – 0) = 50/3 = 16 2/3 paramecia per day. The two points we used here were (0,300) and (3,350).

This eliminates choice (C).

(5) It should be noted that we do not actually need to compute the growth rates to determine which growth rate is higher. We can simply look at the “steepness” of the two curves. An easy way to do this is to draw a “tangent line” to each curve at the point where we wishto examine the growth rate. Here is an example of such an analysis at t = 2:

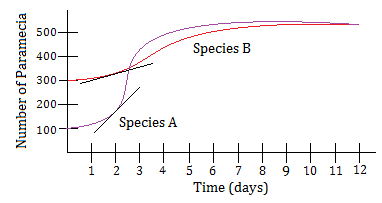
Notice that the tangent line for species A rises faster than the tangent line for species B. This shows that species A is growing faster than species B at time t = 2.

(6) We can use a similar analysis as we did in note 5 to see that the growth rate is decreasing for each species between times t = 4 and t = 12. Here as an example of such an analysis for Species B:

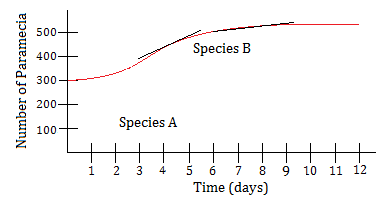
Notice that the tangent line at time t = 4 is steeper then the tangent line at time t = 8. This suggests that the growth rate of species B is decreasing from t = 4 to t = 12.

If you liked this article, please share it with your Facebook friends:

And don’t forget to check out my social media pages:

SAT Math Problem with Solution

July 5, 2016

SAT Math Problem with Solution

Today I would like to provide you with a sample question and solution for the revised SAT. This one is a Level 2 Problem Solving question.

Level 2 Problem Solving

A chemist has a supply of 5.2 liter bottles of a certain solvent that must be shipped to a central warehouse. The warehouse can accept the solvent at the rate of 3 hectoliters per minute for a maximum of 8 hours per day. If 1 hectoliter equals 100 liters, what is the maximum number of bottles that the warehouse could receive from the chemist each day.

(A) 461
(B) 462
(C) 27,692
(D) 83,200

Solution: The warehouse can receive 3 ∙ 60 ∙ 8 hectoliters of the solvent per day, or equivalently, 1440 ∙ 100 = 144,000 liters of the solvent per day. Therefore the number of bottles that can be accepted each day is 144,000/5.2 which is approximately 27,692.30769. The maximum number of bottles that the warehouse can accept in one day is therefore 27,692, choice (C).

Notes: (1) Since there are 60 minutes in an hour, “3 hectoliters per minute” is the same as 3 ∙ 60 = 180 hectoliters per hour.

Similarly, since the warehouse can accept the solvent for a maximum of 8 hours per day, “180 hectoliters per hour” is equivalent to a maximum of 180 ∙ 8 = 1440 hectoliters per day.

(2) In the above solution we combined the two conversions given in note 1 into a single conversion: “3 hectoliters per minute” is equivalent to a maximum of 3 ∙ 60 ∙ 8 = 1440 hectoliters per day.

(3) Since 1 hectoliter equals 100 liters, we can convert hectoliters to liters by multiplying by 100. So 1440 hectoliters is equal to 1440 ∙ 100 = 144,000 liters.

(4) We can convert between hectoliters and liters more formally by setting up a ratio. The two things being compared are “liters” and “hectoliters.”

liters 100 x
hectoliters 1 1440

Now draw in the division symbols and equal sign, cross multiply and divide the corresponding ratio to find the unknown quantity x.

100/1 = x/1440

1x = 100 ∙ 1440

x = 144,000

(5) Instead of converting 1440 hectoliters to 144,000 liters, and then dividing by 5.2, we can instead convert 5.2 liters to hectoliters, and then divide 1440/.052, giving the same answer of 27,692, choice (C).

If you liked this article, please share it with your Facebook friends:

For daily SAT preparation, take a look at the Get 800 collection of SAT math prep books.

SAT Math Problems

July 4, 2016

SAT Math Problems

Today I would like to give you two SAT math questions. Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve each of these problems. I will begin giving full solutions to these problems tomorrow.

Level 2 Problem Solving

(A) 461
(B) 462
(C) 27,692
(D) 83,200

Level 2 Data Analysis

Hard Geometry Problem with Solution

for the SAT

Yesterday I gave you a Level 4 Geometry problem for the revised SAT to try. Today I will provide a solution for this problem. If you have not yet attempted the problem go back and take a look at it first so you can try it on your own. Here is the link: Hard Geometry Problem for the Revised SAT

Level 4 – Geometry

Here is the problem once again followed by a solution:

The head of a copper “hexagon head screw bolt” (one cross section of which is shown above) has the shape of a cylinder with a hole shaped like a regular hexagon. The cylindrical head is 2 cm thick with a base diameter of 3 cm. The hexagonal hole is only half the thickness of the entire head, and each side of a hexagonal cross section has a length of 1 cm. Given that the density of copper is 8.96 grams per cubic cm, and density is mass divided by volume, find the mass of the head to the nearest gram.

Solution: We first compute the volume of the head. There are two parts to the volume.

The bottom half of the head is a cylinder with height 2/2 = 1 cm and base radius 3/2. It follows that the volume is

V = πr²h = π(3/2)²(1) = 9π/4 cm³.

The top half of the head consists of the same cylinder as the bottom half, but this time we have to subtract off the volume of a hexagonal prism. The regular hexagonal face can be divided into 6 equilateral triangles, each with area

A = s²√3/4 = 1²√3/4 = √3/4.

So the volume of the hexagonal prism is

V = Bh = (6√3/4)(1) = 3√3/2 cm³

and the volume of the top half of the head is

9π/4 – 3√3/2 cm³

It follows that the total volume of the head is

9π/4 + (9π/4 – 3√3/2) = 18π/4 – 3√3/2 = (9π – 3√3)/2 cm³.

Finally,

D = M/V → 8.96 = M / [(9π – 3√3)/2] → M = 8.96 ∙ (9π – 3√3)/2 ≈ 103.39 grams.

To the nearest gram, the answer is 103.

For an even more detailed solution to this problem check out New SAT Math Problems arranged by Topic and Difficulty Level.

Feel free to add your own solutions to the comments.

$500 New SAT Math Problems$