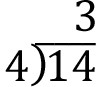500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

AP Calculus BC Geometric Series Problem

With Solution

Yesterday I gave an AP Calculus BC problems involving a geometric series. You can find that post here: AP Calculus BC Problem – Geometric Series.

Today I will provide a solution to that problem. First, here is the question one more time.

Level 2 Series

 

If g is the function given above, then g(π/3) =

(A) 3
(B) 1
(C) 3/4
(D) 1/2

Solution:








Note:

is an infinite geometric series with first term a = 3/4  and common ratio r = 3/4. Watch the video above for more information on geometric series.

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

AP Calculus BC Problem- Geometric Series

AP Calculus BC problems involving series tend to be difficult for students. I thought I would start things off easy today with a level 2 problem involving geometric series. Those of you that have forgotten the basics of geometric series should find the video above helpful.

Let’s now try an AP Calculus BC series problem. AB students do not need to worry about this one. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 2 Series

 

If g is the function given above, then g(π/3) =

(A) 3
(B) 1
(C) 3/4
(D) 1/2

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

Remainder Problems – Part 3

Welcome to the third and final part of this thread on remainder problems. In the first part we discussed some calculator algorithms for finding remainders. You can review that article here: SAT Remainder Problems – Part 1

Yesterday we discussed the cyclical nature of remainders. You can review that article here: SAT Remainder Problems – Part 2

I decided to spend three posts on this subject because many of my students in a mid-level scoring range seem to have a difficult time with ACT and GRE remainder questions.

Solution To Last Week’s Remainder Problem

So where were we? I left you with an ACT math problem to solve using the information I provided regarding the cyclical nature of remainders. Let’s find out how you did.

The problem again:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

Solution: We first find the least positive integer greater than 4 that is divisible by both 6 and 8. This is the least common multiple of 6 and 8 which is 24.

We now simply add the remainder.

24 + 4 = 28.

Thus, the answer is 28.

If you don’t know how to find the least common multiple of two numbers, it’s okay. If you’re taking the ACT, you can just let your TI-84 calculator do it for you. In your calculator press MATH, scroll right to NUM, and press 8 for lcm. Then type 6,8) and you will get an output of 24. So lcm(6,8)=24.

If you are taking the GRE, or you just want to learn other ways to compute the lcm, see the following article: Greatest Common Divisor (GCD) And Least Common Multiple (LCM)

Remainders In Disguise

Test makers’ love to put their remainder problems in disguise. In fact, many remainder problems on standardized tests do not even have the word “remainder” in the question! So how can you be expected to know when to find a remainder? The answer is quite simple. If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Remember this and you will recognize a remainder problem every time. In fact, this is such a key point I am going to repeat this in bold for you!

If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Let’s take a look at a standard example of such a question:

Example

Cards numbered from 1 through 2013 are distributed, one at a time, into nine stacks. The card numbered 1 is placed on stack 1, card number 2 on stack 2, card number 3 on stack 3, and so on until each stack has one card. If this pattern is repeated, each time beginning with stack one, on which stack will the card numbered 2013 be placed?

A. 3^rd stack
B. 4^th stack
C. 5^th stack
D. 6^th stack
E. 7^th stack

Solution: We are actually being asked to find the remainder when 2013 is divided by 9. Let’s do this using the first calculator algorithm that I showed you.

Step 1: Perform the division in your calculator

2013/9 ~ 223.667

Step 2: Multiply the integer part of this answer by the divisor:

9*223 = 2007

Step 3: Subtract this result from the dividend to get the remainder:

2013 – 2007 = 6.

So the card numbered 2013 will be placed on the 6^th stack, choice D.

Notice that the word remainder is never mentioned in this problem. The giveaway that this is a remainder problem in disguise is at the beginning of the last sentence where it says “If this pattern is repeated…”

So this is the end of this three part thread on remainders.

More Remainder Problems with Explanations

If you are preparing for the ACT, the GRE, or an SAT math subject test, you may want to take a look at one of the following books.

If you liked this article, please share it with your Facebook friends:

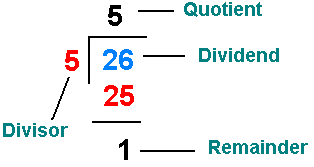Remainder Problems – Part 2

Last week I introduced the idea of solving remainder problems without using long division. We may as well take advantage of the fact that we can use a calculator on the ACT (a TI-84 or equivalent) and GRE (the basic calculator they give you) to solve seemingly difficult math questions with ease. If you haven’t done so already, please read part 1 before continuing with this article: Remainder Problems – Part 1

Solution To Yesterday’s Problem

Yesterday I left you with a cliffhanger of a problem to solve with your calculator. Below is the solution. Let’s see if you got the problem correct and which method you used to solve the problem.

Here is the question again:

What is the remainder when 15,216 is divided by 73?

If you recall I gave three methods to solve such a problem, the first of which is by using long division. Since this post is about solving problems without using long division, let’s skip that method and jump straight to the much quicker and more efficient calculator algorithms – great for use on test day!

Method 2 – First Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Multiply the integer part of this answer by the divisor:

73*208 = 15,184

Step 3: Subtract this result from the dividend to get the remainder:

15,216 – 15,184 = 32.

And here is an alternative:

Method 3 – Second Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Subtract off the integer part of this result:

ANS – 208 ~ .438

Step 3: Multiply this result by the divisor:

73*ANS = 32.

Did you get this problem correct? Which method did you use? Try using both methods and then choose the one that you will be most comfortable with on the day of your standardized math test. And remember: the best way to get comfortable with a new technique is to practice with it!

The Cyclical Nature Of Remainders

Today let’s talk a bit about the cyclical nature of remainders. If you can understand this, then solving many ACT and GRE remainder problems will become second nature to you.

Let’s see what happens when we divide various positive integers by the number 3.

When we divide 3 by 3 we get a quotient of 1 and a remainder of 0. In other words,

3 = 3(1) + 0.

When we divide 4 by 3 we get a quotient of 1 and a remainder of 1. In other words,

4 = 3(1) + 1.

When we divide 5 by 3 we get a quotient of 1 and a remainder of 2. In other words,

5 = 3(1) + 2.

Now we have to be careful. When we divide 6 by 3, the quotient is now 2 and the remainder is 0. That is, 6 = 3(2) + 0.

So the remainders start over. When dividing by 3, the remainders cycle from 0 to 2 then back to 0.

0, 1, 2, 0, 1, 2, 0, 1, 2…

The easiest way to find a positive integer that has a certain remainder is to start with one that is evenly divisible, and then add the remainder. For example, suppose we want to find a positive integer that has a remainder of 7 when divided by 9. We can start with a number evenly divisible by 9, such as 9 itself, and then add 7. Since 9 + 7 = 16, we see that 16 is such a number. In fact,

16 = 9(1) + 7.

That is, when we divide 16 by 9 the quotient is 1 and the remainder is 7.

Since 18 is also divisible by 9, 18 + 7 = 25 is another positive integer that has a remainder of 7 when divided by 9. There are infinitely many possibilities!

Note that 0 is actually divisible by 9 as well. Indeed, we have

0 = 9(0) + 0.

Thus, 0 + 7 = 7 is a number that gives a remainder of 7 when divided by 9. In other words, we can actually just use the remainder itself!

Exercise

Now let’s see if you can apply this information to an actual ACT math problem. Here is a nice medium difficulty problem I like to give to my own ACT math students:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

Do you know how to go about solving this? You can find the answer in part 3 of this article here: Remainder Problems – Part 3

More Remainder Problems with Explanations

If you are preparing for the ACT, the GRE, or an SAT math subject test, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

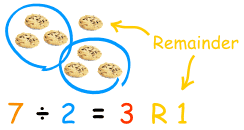Can We Solve Remainder Problems

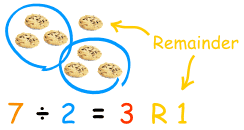
Without Using Long Division?

For the next three days I would like to help you to understand math problems involving remainders. These types of problems appear on standardized tests such as the ACT, GRE, and SAT math subject tests.

ACT and GRE math problems with remainders seem to give students a difficult time. This is mostly because a fundamental step in solving the problem is often missed – performing long division.

You cannot solve a remainder problem by simply dividing in your calculator. There are, however, calculator algorithms that can give you the answer very quickly. We will talk about these a bit later in this post.

A common error that students make is to perform a division calculation on their calculator, and simply take the first number after the decimal point and use this digit as the answer to the problem. This will usually result in a wrong answer.

Example

Suppose we are asked “Find the remainder when 14 is divided by 4.”

In your calculator, 14/4 = 3.5.

Penciling the number 5 as your answer would be incorrect – seriously incorrect. This “5” is actually part of the answer to the question “What is 14 divided by 4?” But it has nothing to do with the remainder.

Students that are currently scoring in the mid-range in ACT/GRE math seem to have the biggest problem with remainder questions. Many cannot perform long division correctly, and some do not even realize that long division is needed. This keeps many students from getting their scores to the next level.

Let’s take a look at how we can solve the problem of finding the remainder when 14 is divided by 4 in three different ways. This problem may seem very basic for some of you, but let’s go over it anyway to make sure we have a strong foundation before solving more difficult remainder problems.

Method 1 – Long Division: So 4 goes into 14 three times with 2 left over. In other words, 14 = 4(3) + 2. So we see that the remainder when we divide 14 by 4 is 2.

Let’s break this down step by step:

Count the number of groups of 4 objects that can be formed from 14 objects. Place this number over the 4 that is inside the division symbol.

Multiply this resulting  number 3 by the divisor 4. Place this number below the 4 that is inside the division symbol.

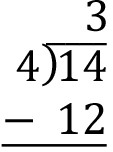
Subtract the resulting number 12 from the dividend 14.

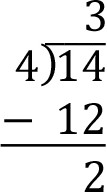
The quotient 3 appears above the division symbol and the remainder 2 appears at the bottom.

Below is a visual representation of 14 divided by 4. In the figure below we are grouping 14 objects 4 at a time. Note that we wind up with 3 groups (the quotient) and 2 extra objects (the remainder).

Method 2 – First Calculator Algorithm:

Step 1: Perform the division in your calculator:

14/4 = 3.5

Step 2: Multiply the integer part of this answer by the divisor:

4*3 = 12

Step 3: Subtract the above result from the dividend to get the remainder:

14 – 12 = 2.

Method 3 – Second Calculator Algorithm:

Step 1: Perform the division in your calculator:

14/4 = 3.5

Step 2: Subtract off the integer part of this result:

ANS – 3 = .5

Step 3: Multiply this result by the divisor:

4*ANS = 2.

Note that these calculator algorithms work exactly the same no matter how large the numbers are that you are dividing.

Exercise

As an additional exercise you should try to find the remainder when 15,216 is divided by 73 by using one of these calculator algorithms. Figure out which of the two algorithms you prefer. You can find solutions here: SAT Remainder Problems – Part 2

More Remainder Problems with Explanations

If you are preparing for the ACT, the GRE, or an SAT math subject test, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

AP Calculus AB Related Rates Problem with Solution

Yesterday I posted a Level 4 related rates problem for the AP Calculus AB exam (although this problem is a pretty standard Calculus problem that you may come across in any Calculus course). You can see that post here: AP Calculus AB Problem – Related Rates

Today I would like to provide a full explanation for this problem. Here is the problem one more time:

The radius of a spherical balloon is decreasing at a constant rate of 0.5 centimeters per second. At the instant when the volume V becomes 288π cubic centimeters, what is the rate of decrease, in square centimeters per second, of the surface area of the balloon?

(A) 24π
(B) 48π
(C) 64π
(D) 72π

Solution: Recall that the volume of a sphere with radius r is

V = 4/3 πr³,

and the surface area of a sphere with radius r is

S = 4πr².

We are given that  dr/dt = –0.5, and we are being asked to find  dS/dt  when V = 288π.

First note that when V = 288π, we have

288π = 4/3 πr³
3/4 ⋅ 288π = πr³
216 = r³
6 = r

Now,

dS/dt = 8πr ⋅ dr/dt = 8πr(–0.5) = –4πr.
dS/dt (at r = 6) = –4π(6) = –24π.

So the surface area of the balloon is decreasing at a rate of 24π cm²/sec. Therefore, the answer is choice (A).

Notes: (1) Observe that one can get the formula for the surface area of a sphere by differentiating the formula for the volume of a sphere. This is just a little trick that can be used to reduce the number of formulas to memorize.

(2) Remember that the word rate generally indicates a derivative. “Increasing at a rate of” indicates a positive derivative, and “decreasing at a rate of” indicates a negative derivative.

(3) A radius is a length and is therefore measured in single units (in this case centimeters). Area (and in particular, surface area) is measured in square units. Volume is measured in cubic units.

The type of units being mentioned usually gives a big hint as to what measurement is being given or asked for.

(4) This is a related rates problem. In a related rates problem we differentiate the independent and dependent variables with respect to a new variable, usually named t, for time.

(5) A related rates problem can be pictured as a dynamic (moving) process that gets fixed at a specific moment in time.

For this problem we can picture a sphere shaped balloon deflating. We then freeze time at the moment when the volume is 288π cm³.

At this moment in time we want to know what the rate of decrease of the surface area is. The word “rate” indicates that we want the derivative of surface area with respect to time,  dS/dt.

Don’t forget to apply the chain rule when differentiating the right hand side. In this case, the derivative of r is  dr/dt.

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

AP Calculus AB – Related Rates 

Students that are taking AP Calculus (or any Calculus course) usually find related rates word problems to be difficult. The concept however is really not so hard to understand. The idea is that you have two or more quantities that are changing with time, and those two quantities are related in some way. In a Precalculus problem, we would explore the relationship between those two quantities. But in a Calculus problem we explore the relationship between the rates at which those quantities are changing.

Let’s try a typical AP Calculus AB related rates problem (note that any Calculus AB problem can also appear on the BC exam). I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 4 Related Rates Problem

The radius of a spherical balloon is decreasing at a constant rate of 0.5 centimeters per second. At the instant when the volume V becomes 288π cubic centimeters, what is the rate of decrease, in square centimeters per second, of the surface area of the balloon?

(A) 24π
(B) 48π
(C) 64π
(D) 72π

More AP Calculus Problems with Explanations

If you are preparing for one of the AP Calculus exams, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends:

The Differences Between the ACT and the SAT

The ACT and SAT are both standardized tests that are used for college admissions. Students should be aware that they have a choice in which standardized test they choose to take. Years ago, the SAT was the more popular choice on the east and west coasts, and the ACT was more popular throughout the rest of the country. Last year, when the College Board debuted a new version of the SAT, these numbers changed significantly. In 2016, more than 2 million high schools students took the ACT and slightly less than a million-and-a-half students took the “new” SAT. But every student should realize that the final decision as to which test to focus on is entirely up to them. This article provides important information about the differences between the two tests so that you can make a more well-informed decision.

Test Length and Structure

The ACT consists of 5 sections. Only 4 of these sections must be completed. The fifth section – writing – is optional. For the required sections, there is a 45 minute english section, a 60 minute math section, a 35 minute reading section, and a 35 minute science section. You are given 40 minutes for the optional writing section. This gives a total required testing time of 45 + 60 + 35 + 35 = 175 minutes, or 2 hours and 55 minutes. With the optional writing section, the total testing time increases to 3 hours and 35 minutes.

The SAT is a longer test than the ACT. It also consists of 5 sections, one being optional (the essay). For the required sections, there is a 65 minute reading section, a 35 minute grammar section, a 25 minute math section where a calculator is not allowed, and a 55 minute math section where a calculator is allowed. You are given 50 minutes for the optional essay section. This gives a total required testing time of 65 + 35 + 25 + 55 = 180 minutes, or 3 hours. With the optional essay, the total testing time is 3 hours and 50 minutes.

On both the ACT and SAT, the essay is optional, and it is NOT factored into the final score. Many schools do however require the essay, so if you are not yet certain about all the schools you will be applying to you may want to take the essay as a precaution.

Scoring

The ACT is graded out of 36 points. The overall score is the average of the scores on each of the 4 required sections. Each of these is also graded out of 36 points.

The SAT is graded out of 1600 points. The overall score is the sum of the scores for verbal and math each consisting of a total of 800 points (note that the verbal score is made from both the reading and grammar sections, and the math score is made from the two math sections).

Conversion charts are easy to find for comparing ACT and SAT scores. For example, take a look here: ACT/SAT Conversion Chart (pages 7 and 15)

Pacing

The ACT requires a faster pace than the SAT to get through each section. Let’s look at math as an example, and assume that a student is pacing themselves to answer every single math question. The student has an average of 1 minute to complete each math question on the ACT, compared to an average of 1 minute and 15 seconds per question on the “no calculator” math section on the SAT, and an average of about 1 minute and 25 seconds per question on the “calculator allowed” math section of the SAT.

It should be noted that for many students it may be counterproductive to attempt every question on a standardized test, but this kind of advice lies outside the scope of this article.

Science Section

The ACT has a science section and the SAT does not. It should be noted that the science section is really more about reading comprehension and interpreting data found in charts, figures and tables. Very little knowledge of science is actually required (although it could be argued that students with a stronger science background are at an advantage here).

Free Response Questions

Both math sections on the SAT have free response questions, also known as “grid-ins.” In these questions the student must give a numerical answer without having any choices to choose from.

Calculator Policy

On the ACT you can use a calculator for every question. There are two math sections on the SAT, one where a calculator can be used, and one where a calculator cannot be used. Students that are very calculator dependent tend to have a lot of trouble with the “no calculator” SAT math section.

Difficulty versus Trickiness and Complexity in Math

ACT math problems tend to be more straightforward than SAT problems, whereas some SAT math problems are more complex and may take more time to answer.  It is often much easier to understand ACT questions upon a first reading, whereas SAT questions tend to seem more confusing at first.

Many SAT math problems now go out of their way to model “real life” situations. In my opinion these types of questions tend to be more confusing and harder to read. The SAT also has more “multi-step” problems than the ACT (especially the more difficult problems that appear later in each section). You may have to complete 2, 3, or 4 distinct tasks to get to a solution.

Mathematics Covered

The ACT and SAT cover many of the same topics, but there are some differences. The following topics are covered on the ACT, but not on the SAT.

• Arithmetic
• Divisibility, Primes, GCD, LCM
• Sequences and Series (especially arithmetic and geometric sequences)
• Counting Problems
• Laws of Sines and Cosines
• Logarithms

Although there are no specific topics on the SAT that are not on the ACT, the SAT does place a heavier emphasis on Data Analysis, systems of equations and inequalities, and some more advanced precalculus concepts such as completing the square and divison of polynomials.

The ACT places a much heavier emphasis on Geometry than the SAT. Up to 50% of the ACT math questions can be Geometry and Trigonometry questions (much more Geometry than Trigonometry), whereas just a few math questions on the SAT  will come from these topics.

Final Note

The best way to decide which test you should focus on is to take a practice test for both the ACT and the SAT. I strongly recommend using official practice tests from the testmakers themselves. Use a score comparison chart to compare your scores and you will see firsthand where your strengths lie.

Once you decide which test you will focus on make sure you take some time to prepare. I always recommend preparing for 10 to 20 minutes per day over a period of 3 to 4 months.

If you decide that you will be taking the SAT, I suggest you take a look at my “Get 800” collection of SAT math prep books, and if you decide that you will be taking the ACT, check out 320 ACT Math Problems arranged by Topic and Difficulty Level. Click the picture below for details.

If you liked this article, please share it with your Facebook friends:

AP Calculus BC Exam Changes

The AP Calculus exams are going through a few small changes, and so I have been updating my AP Calculus prep books to account for these changes. The revised version of the book for the BC exam is now ready. Here is a link to the book’s Amazon page: 320 AP Calculus BC Problems

The following changes are being made to the AP Calculus BC exam beginning with the 2016-2017 academic year:

1. Multiple choice questions will have only 4 answer choices instead of 5.
2. The distribution of multiple choice questions will be modified slightly as follows: The “no calculator allowed” portion (Part A) will now consist of 30 questions (up from 28) and you will have 60 minutes (up from 55). The “calculator required” portion (Part B) will now consist of 15 questions (down from 17) and you will have 45 minutes (down from 50).
3. The following topics will be added: limit comparison test, absolute and conditional convergence, and the alternating series error bound.

My New AP Calculus Social Media Accounts

Don’t forget to like my new AP Calculus Facebook page, and follow my new AP Calculus Twitter account.

If you think your friends might be interested in this information, please share it with them on Facebook:

Thank you all for your continued support!

Hard SAT Math Problem with Solutions

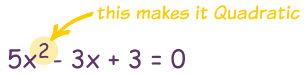
Yesterday I gave you a Level 5 SAT math problem. Today I will provide solutions for this problem. If you have not yet attempted the problem go back and take a look at it first so you can try it on your own. Here is the link: Hard SAT Math Problem

Level 5 – Passport to Advanced Math

Here is the problem once again followed by several solutions:

If x² – 8x = 209 and x < 0, what is the value of |x + 3| ?

Algebraic solution: Let’s attempt to factor the equation. We begin by subtracting 209 from each side to get x² – 8x – 209 = 0. We now factor the left hand side to get (x – 19)(x + 11) = 0.

So x = 19 or x = -11. Since we are given x < 0, we use x = -11.

Finally we have |x +3| = |-11 + 3| = |-8| = 8.

Notes: (1) There are several ways to solve a quadratic equation. A few are by (i) factoring, (ii) completing the square, (iii) the quadratic formula, (iv) guessing and checking, (v) creating a table of values in your calculator, (vi) using the graphing features of your calculator.

(2) Whenever you solve a quadratic equation by factoring or by using the quadratic formula, you need to bring everything over to one side of the equation first, leaving 0 on the other side.

(3) It can seem very difficult at first to find the factors of 209, but the following trick can help you find the factors a little easier. Since we have 15² = 225 > 209, it follows that if 209 can be factored, then it has a factor less than 15. Furthermore, since every positive integer can be factored as a product of primes, it follows that we need only check prime numbers less than 15. So we can simply check 209 for divisibility by 2, 3, 5, 7, 11, and 13.

We can use standard divisibility tricks to eliminate 2, 3, and 5 right away (if you don’t know these tricks you can learn about them here: Divisibility Tricks). You may want to try 11 next since it is pretty easy to divide by 11. In this case we have 209/11 = 19. So 209 = 11 ∙ 19.

If we happen to be allowed to use a calculator for this problem, then we could divide 209 by these numbers very quickly.

(4) Several more notes giving more insight into this solution can be found in New SAT Math Problems arranged by Topic and Difficulty Level.

Solution by guessing and checking: If we are allowed to use our calculator, there are several other ways to solve the given equation for . One way is to simply guess and check negative values for x. For example if we substitute -3 in for x on the left hand side of the equation we get (-3)^2 – 8(-3) = 33, which is too small. So let’s try x = -8 next: (-8)^2 – 8(-8) = 128 . This is still too small, but we’re heading in the right direction. We try x = -11 to get (-11)^2 – 8(-11) = 209.

It works. So x = -11  and we have |x +3| = |-11 + 3| = |-8| = 8.

For additional solutions to this problem such as completing the square, using the quadratic formula, creating a table of values, and by graphing check out New SAT Math Problems arranged by Topic and Difficulty Level. 

Feel free to add your own solutions to the comments. 

More Hard SAT Math Practice Problems

If you are preparing for the SAT or another standardized test such as the ACT or GRE, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

If you think your friends would like to try these problems, please share:

Speak to you soon!