500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

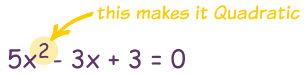Hard SAT Math Problem

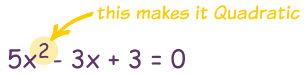
Hello everybody. I think it’s time for an example of a difficult math problem that may show up on the new SAT. This one is a Level 5 free response question (or grid-in).

Level 5 – Passport to Advanced Math

If x² – 8x = 209 and x < 0, what is the value of |x + 3| ?

Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve the problem. I will post several solutions to this problem next week.

More Hard SAT Math Practice Problems

If you are preparing for the SAT or another standardized test such as the ACT or GRE, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

If you think your friends would like to try these problems, please share:

Speak to you soon!

320 AP Calculus BC Problems – New Edition

Today I would like to announce the release of the second edition of  320 AP Calculus BC Problems arranged by Topic and Difficulty Level.

The paperback is now on sale on Amazon for only $5.74.

This sale will run for just a few hours, and once the sale ends the price will go up to $34.99. If you want to take advantage of the sale price I strongly recommend you purchase the book right away.

Click the following link to get to the book’s Amazon page: 320 AP Calculus BC Problems, 2nd Edition

Note that this book is for preparing for the May 2017 exam.

As an additional incentive to purchase this book today, I will also give you an additional book for FREE as a downloadable PDF file. You can choose ANY of my other books. So if you would like a different book, go ahead and purchase this one (as soon as it is available), forward me your Amazon confirmation email (to steve@SATPrepGet800.com) and let me know which of my books you would like for free. You will be provided with a link to download your additional free book. This offer is available until the end of today (June 20, 2016).

You can choose any book on my product page.

AP Calculus BC Exam Changes

i created new editions of my AP Calculus books because the AP Calculus exams are going through a few small changes. My new editions have been created to reflect these changes.

The following changes are being made to the AP Calculus BC exam beginning with the 2016-2017 academic year:

1. Multiple choice questions will have only 4 answer choices instead of 5.
2. The distribution of multiple choice questions will be modified slightly as follows: The “no calculator allowed” portion (Part A) will now consist of 30 questions (up from 28) and you will have 60 minutes (up from 55). The “calculator required” portion (Part B) will now consist of 15 questions (down from 17) and you will have 45 minutes (down from 50).
3. The following topics will be added: limit comparison test, absolute and conditional convergence, and the alternating series error bound.

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Combinations on the ACT and GRE

Today I would like to continue discussing more advanced methods for solving counting problems.

Two days ago we discussed some more basic methods for solving counting problems on the ACT and GRE. These methods can be viewed by clicking the following link: Listing and the Counting Principle

And yesterday we talked about permutations. This article can be viewed here: Permutations 

Today I want to focus on another more advanced counting technique – Combinations.

Combinations

A combination is just a subset containing a specific number of the elements of a particular set. The number of combinations of n things taken r at a time is

For example, the number of combinations of {1, 2, 3} taken 2 at a time is

These combinations are 12, 13, and 23.

Note that 21 is the same combination as 12 (but 12 and 21 are different permutations). More on this below…

Just like the permutation formula, you do not need to know the combination formula for the ACT. You can do this computation very quickly on your TI-84 graphing calculator. To compute ₃C₂, type 3 into your calculator, then in the Math menu scroll over to Prb and select nCr (or press 3). Then type 2 and press Enter. You will get an answer of 3.

Difference Between Permutations And Combinations

Let me quickly tell you the difference between permutations and combinations: “Permutation” is just a fancy word for arrangement. Whenever you are counting the number of ways to arrange things you can use the permutation formula that I shared with you last week (or better yet the nPr feature in your calculator). So if you want to “order” things, “stack” things, “rearrange” things, choose specific tasks for people, etc, you would use permutations.

“Combinations” are used when you want to group things together without putting them in any specific order. This happens when you split a group of objects into two piles, or form a committee of people, for example.

So the numbers 12 and 21 are different permutations, but the same combination.

Here is a very basic combination problem:

Example 1

How many committees of 4 people can be formed from a group of 9?

The order in which we choose the 4 people does not matter. Therefore this is the combination ₉C₄= 126.

Here is our first standardized test math problem where combinations can be used:

Permutations on the ACT and GRE

Today I would like to talk about some more advanced methods for solving Counting Problems. The content presented here and in tomorrow’s post is meant for more advanced students whose current ACT math score is at least a 25 or whose GRE score is at least a 148.

Last week we discussed some more basic methods which can be viewed by clicking the following link: Listing and the Counting Principle.

Please quickly review yesterday’s post before going on to the content below. Five minutes of review will really solidify the concepts from that post and will make the information in this post easier to learn.

Factorials

First let’s discuss factorials. The factorial of a positive integer n, written n!, is the product of all positive integers less than or equal to n.

n! = 1·2·3…n

0! is defined to be 1, so that n! is defined for all nonnegative integers n.

The definition for 0! may seem strange to many of you. Mathematicians have made this definition so that the formula n! = n(n – 1)! will be true for all positive integers n. Note that with this definition 1! = 1·0!

Permutations

Now a permutation is just an arrangement of elements from a set. The number of permutations of n things taken r at a time is

For example, the number of permutations of {1, 2, 3} taken 2 at a time is

These permutations are 12, 21, 13, 31, 23, and 32.

The good news is that on the ACT you do not need to know the permutation formula. You can do this computation very quickly on your graphing calculator. To compute ₃P₂, type 3 into your calculator, then in the Math menu scroll over to Prb and select nPr (or press 2). Then type 2 and press Enter. You will get an answer of 6. On the GRE, of course, you would not be able to use this calculator feature.

As always, let’s internalize these principles by putting them into practice. Here is a simple counting problem that can be solved using permutations.

Example 1

Four different books are to be stacked in a pile. In how many different orders can the books be placed on the stack?

Solution by listing: Okay, now you could imagine stacking the books in different ways. Let’s try this by listing the different permutations. To distinguish the books let’s make one red, one blue, one yellow, and one green. Let’s abbreviate each book’s color by using its first letter.

rbyg rbgy rybg rygb rgby rgyb
bryg brgy byrg bygr bgry bgyr
yrbg yrgb ybrg ybgr ygrb ygbr
grby gryb gbry gbyr gyrb gybr

We now see that there are 24 arrangements.

The thing is that on a standardized test I would rather not take the time to write out each permutation. There is a chance, under the time pressure of the test, that an error could be made or too much time could be spent checking that I have not duplicated any of the permutations.

Here are two more solutions that are much more efficient. First we can use the counting principle that we reviewed in last week’s post:

Solution using the counting principle:  There are 4 possible books for the bottom of the stack. After placing the first book, there are 3 possible books that can go on top of the bottom book, then 2 books for the next position, and then 1 book for the top of the stack. Using the counting principle we get a solution of (4)(3)(2)(1) = 24 arrangements.

Or we can solve this problem even faster by using our new knowledge of permutations:

Solution using permutations:  There are 4 books, and we are arranging all 4 of them. Therefore there are ₄P₄ = 4! = (1)(2)(3)(4) = 24 arrangements.

I think you would agree that the last solution is much faster than the original solution by listing.

Example 2

Three light bulbs are placed into three different lamps. How many different arrangements are possible for three light bulbs of different colors – one red, one green, and one yellow?

Solution by listing: Again, we can list all the possibilities, abbreviating each color by using the first letter.

rgy ryg gry gyr yrg ygr

We can easily see that there are 6 arrangements.

And again, we can also use the counting principle:

Solution using the counting principle: There are 3 possible lamps to place the red bulb in. After placing the red bulb, there are 2 lamps to place the green bulb in. Finally, there is 1 lamp left to place the yellow bulb in. By the counting principle we get (3)(2)(1) = 6 arrangements.

And finally we can solve this problem very quickly using our knowledge of permutations:

Solution using permutations: There are 3 light bulbs, and we are arranging all 3 of them. So the number of arrangements is ₃P₃ = 3! = 1·2·3 = 6.

Where To Find More Practice Problems

If you are preparing for the ACT, GRE or any other standardized test that has counting problems, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

Counting Problems on the ACT and GRE

Today I would like to start a thread on ‘counting.” Although counting sounds like it should be an easy concept, students tend to find math problems on standardized tests such as the ACT and GRE that involve counting among the most difficult.

Writing A List

Okay let’s start with the most basic strategy, namely ‘writing a list’… Sometimes the easiest way to count the number of possibilities is to simply list them all. When doing this it is important that you have a systematic way of forming your list. This will reduce the likelihood of missing something, or listing something twice.

With that said, let’s look at a simple counting problem:

Example 1

A menu lists 2 meals and 3 drinks. How many different meal drink combinations are possible from this menu?

Some of you may already be able to solve this problem very quickly, but let’s first solve this by writing a list.

Let’s make up 2 meals and 3 drinks, say chicken and fish for the meals, and water, soda, and juice for the drinks. Now let’s list all meal-drink combinations. To save time we will abbreviate each meal and drink by using its first letter.

cw  cs  cj  fw  fs  fj

We see that there are 6 meal-drink combinations.

Now, as many of you probably already realize, we can actually solve this problem very quickly by using the counting principle.

(2)(3) = 6

The Counting Principle

The counting principle says that if one event is followed by a second independent event, the number of possibilities is multiplied. The 2 events in the above problem are “choosing a meal,” and “choosing a drink.”

Now let’s get a little more advanced and look at the counting principle in full generality.

More generally, the counting principle says that if E₁, E₂, …, E_n are n independent events with m₁, m₂, …, m_n possibilities, respectively, then event E₁ followed by event E₂, followed by event E₃, …, followed by event E_n has  m₁∙m₂ ∙∙∙ m_n possibilities.

My head is spinning after looking at all these E’s and m’s, so let’s try a problem to see this principle in action.

Example 2

How many integers between 9 and 300 have the tens digit equal to 2, 3, or 4 and the units digit (ones digit) equal to 5 or 6?

Let’s first solve this using the more general version of the counting principle:

There are 2 possibilities for the ones digit (5 or 6). There are 3 possibilities for the tens digit (2, 3, or 4). There are 3 possibilities for the hundreds digit (0, 1, or 2). The counting principle says that we multiply the possibilities to get (2)(3)(3) = 18.

That’s not so bad, is it?

Note that we could also solve this problem by writing a list:

Let’s simply list all the numbers in increasing order:

25  26  35  36  45  46  125  126  135  136  145  146  225  226  235  236  245  246

And that’s it. Once again we see that the answer is 18.

Okay, let’s do a more difficult counting problem. This one is Level 5:

Example 3

How many integers between 3000 and 4000 have digits that are all different and that increase from left to right?

The best way to solve this is by writing a list:

As you can see, there are 20 integers in this list.

It would be good to take note that we only wrote down the necessary information when forming our list. For example, the second entry was just written “7” instead of “3457.” This will save a substantial amount of time.

Also a clear and definite pattern was used in forming this list. In this case the list was written in increasing order. This will minimize the risk of duplicating or leaving out entries.

Follow the advice given here with  similar problems you see on the ACT or GRE and you will be able to answer them quickly and efficiently.

For more advanced counting techniques take a look at my articles on Permutations and Combinations.

Where To Find More Practice Problems

If you are preparing for the ACT, GRE or any other standardized test that has counting problems, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

Recognizing Blocks

Today, let’s discuss a math strategy I like to call “Recognizing Blocks.” This is a strategy that can sometimes be used on standardized tests such as the ACT, SAT, GRE, and AP Calculus exams.

First, let me give my definition of a block: A block is an algebraic expression that appears more than once in a given problem.

Very often in math problems on standardized tests a block can be treated just like a variable. In particular, blocks should usually not be manipulated—treat them as a single unit.

This is simple in theory. Let’s first try it with a basic algebra  problem:

Example 1

If 3x – 5y = 7 , what is the value of 6(3x − 5y) ?

(A) 50
(B) 42
(C) 36
(D) 30
(E) 4

In this example there is a block of 3x – 5y. Let’s look at the following seemingly easier problem:

If a = 7, what is the value of 6a?

The answer to this problem is (6)(7) = 42.

But this is essentially the same problem as the one we were given. We just replaced the block by the variable a. So the answer to the original question is also 42, choice (B).

You can be really sharp by doing this problem in your head in just a few seconds: (6)(7) = 42. choice (B).

Easy, right?

Here is a more difficult problem for you:

Example 2

If b = 7(u + v + x + y +z)/5, then in terms of b what is the average (arithmetic mean) of u, v, x, y, and z?

(A) b/35
(B) b/7
(C) b/5
(D) 5b
(E) 7b

In this example there is a block of a = (u + v + x + y + z)/5 which is precisely the average of u, v, x, y, and z. So solving this problem is the same as solving the following equation for a.

b = 7a

To solve this equation for a we will simply divide both of the sides by 7 to get a = b/7, choice (B).

These problems as relatively straightforward to solve as long as you treat all blocks as variables and do not try to manipulate them.

More Problems Involving Blocks

If you are preparing for the ACT, SAT, GRE, or another standardized test, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

SHSAT Verbal Prep Book

If you or your child are planning to attend one of the specialized high schools in NYC, make sure to get your copy of the SHSAT Verbal Prep Book to Improve Your Score in Two Months. 

Click the following link to get to the book’s Amazon page: SHSAT Verbal Prep Book

For more information on the specialized high schools you may want to take a look at the following page on the Department of Education’s website: Specialized High Schools

The material in this SHSAT prep book includes:

• 40 scrambled paragraphs
• 6 logical reasoning practice quizzes
• 15 reading passages
• Full explanations for all questions.

Take a look at my product page to see all of my books: Get 800 Product Page

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

Thank you all for your continued support!

Changing Averages To Sums

On standardized tests such as the ACT, SAT, and GRE, a problem involving averages often becomes much easier when we first convert the averages to sums. We can easily change an average to a sum using the following simple formula.

Sum = Average · Number

Many problems with averages involve one or more conversions to sums, followed by a subtraction.

Try to answer the following question using this strategy. Do not check the solution until you have attempted this question yourself.

Example 1

The average (arithmetic mean) of three numbers is 100. If two of the numbers are 80 and 130, what is the third number?

(A) 70
(B) 80
(C) 90
(D) 100
(E) 110

In this case we are averaging 3 numbers. So the Number is 3. The Average is given to be 100. Thus, the Sum of the 3 numbers is 10 · 3 = 300. Since two of the numbers are 80 and 130, the third number is 300 – 80 – 130 = 90, choice (C).

Got it? Well here is another, slightly more advanced, problem where this technique is useful:

Example 2

The average of x, y, z  and w is 15 and the average of z and w is 11. What is the average of x and y?

The Sum of x, y, z and w is 15 · 4 = 60. The Sum of z and w is 11 · 2 = 22. Thus, the Sum of x and y is 60 – 22 = 38. Finally the Average of x and y is 38/2 = 19.

Notice how we actually used the formula “Sum = Average · Number” twice here. For those of you that require further clarification, here are the calculations in more detail.

So (x +y)/2 = 38/2 = 19.

Thoughts on this? Still have questions? Post them on my Facebook wall:

320 AP Calculus AB Problems – Just $5.69

Today I would like to announce the release of the second edition of 320 AP Calculus AB Problems arranged by Topic and Difficulty Level. This new edition reflects the changes that will be implemented for the exam being given next May.

The paperback is now on sale on Amazon for only $5.69.

This sale may last for only a few hours, and once the sale ends the price will go up to $34.99. Amazon will automatically raise the price once a predetermined number of copies has been sold. If you want to take advantage of the sale price I strongly recommend you purchase the book now.

Click the following link to get to the book’s Amazon page: 320 AP Calculus AB Problems

As an additional incentive to buy this book, I would like to give you an additional books for FREE as a downloadable PDF file. You can choose ANY of my other books. So if you would like a different book, go ahead and purchase this one, forward me your Amazon confirmation email (to steve@SATPrepGet800.com) and let me know which of my books you would like for free. You will be provided with a link to download your additional free book. This offer is available until the end of today (June 13, 2016).

Take a look at my product page to see all of my books: Get 800 Product Page

AP Calculus AB Exam Changes

The AP Calculus exams are going through a few small changes, and so I have been updating my AP Calculus prep books to account for these changes. The revised version of the book for the AB exam is just about ready, and so today I thought I would focus on the AB exam.

The following changes are being made to the AP Calculus AB exam beginning with the 2016-2017 academic year:

1. Multiple choice questions will have only 4 answer choices instead of 5.
2. The distribution of multiple choice questions will be modified slightly as follows: The “no calculator allowed” portion (Part A) will now consist of 30 questions (up from 28) and you will have 60 minutes (up from 55). The “calculator required” portion (Part B) will now consist of 15 questions (down from 17) and you will have 45 minutes (down from 50).
3. One new topic has been added: L’Hôpital’s rule*

* Note that there have always been problems on the AP Calculus AB exam where L’Hôpital’s rule could be used. The difference now is that problems may show up where L’Hôpital’s rule must be used. This is a very minor addition to the exam.

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hard Trigonometry Problem with Solution for the SAT

Yesterday I gave you a Level 5 trigonometry problem for the revised SAT to try. Today I will provide a solution for this problem. If you have not yet attempted the problem go back and take a look at it first so you can try it on your own. Here is the link: Hard Trigonometry Problem for the Revised SAT

Level 5 – Trigonometry

Here is the problem once again followed by a solution:

It is given that cos x = k, where π < x < 3π/2 and x is the radian measure of an angle. If cos z = –k, which of the following could not be the value of  z ?

(A) x – π
(B) π – x
(C) 2π – x
(D) 3π – x

Solution using coterminal angles and a negative identity: 

cos(2π – x) = cos(x – 2π) = cos x = k ≠ –k.

So 2π – x  could not be the value of z, choice (C).

Notes: (1) For the first equality we used the negative identity

cos(–A) = cos A

(see problem 104 in New SAT Math Problems), together with the fact that

x – 2π = –(2π – x) .

(2) In general we have a – b = -(b – a) . To see this simply distribute:

-(b – a) = –b + a = a – b. 

(3) Using notes (1) and (2) together, we have

cos(2π – x) = cos(-(x – 2π)) = cos(x – 2π).

(4) Several more notes giving more insight into this solution can be found in New SAT Math Problems arranged by Topic and Difficulty Level.

For additional solutions to this problem such as using the cosine difference identity and using the unit circle check out New SAT Math Problems arranged by Topic and Difficulty Level.

Feel free to add your own solutions to the comments.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out the Get 800 collection of SAT math prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!