500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hard Trigonometry Problem

The SAT contains a very small number of trigonometry questions. Today I would like to provide an example of a particularly hard trigonometry problem that could show up.

Level 5 – Trigonometry

It is given that cos x = k, where π < x < 3π/2 and x is the radian measure of an angle. If cos z = –k, which of the following could not be the value of  z ?

(A) x – π
(B) π – x
(C) 2π – x
(D) 3π – x

Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve the problem. I will post several solutions to this problem tomorrow.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out the Get 800 collection of SAT math prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

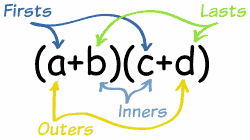To FOIL or Not to FOIL

Most students are familiar with the mnemonic FOIL to help them multiply two binomials (polynomials with 2 terms) together. As a simple example, we have

(x + 1)(x – 2) = x² – 2x + x – 2 = x² – x – 2

I do not particularly like teaching this method for multiplying binomials for the following reasons:

1. This method works ONLY for binomials. It does not extend to polynomials with more than 2 terms.
2. It requires learning something new. There is already an algorithm that works very well that simulates a method students already know.
3. Most students after learning HOW to FOIL will not be able to explain WHY it works.
4. From a theoretical point of view it is inefficient. FIOL is actually the better choice.

Some of you might be saying “But FOIL is so simple and easy to remember. What can possibly be better?” The answer is an algorithm that everyone already knows.

Quick Review of Multiplication

As a quick review, let’s multiply two 2-digit numbers together, say 12 and 32:

12
32

We begin by multiplying the 2 on the bottom by each digit on top, moving from right to left:

12
32
24

We then multiply the 3 on the bottom by each digit on top, moving from right to left. This time as we write the answers we leave one blank space on the right:

12
32
24
36     

Finally, we add:

12
32
24
36     
384

Voila!

A Better Algorithm For Multiplying Polynomials

We are now going to use essentially the same algorithm for multiplying our first two binomials above together. Notice that for multiplying numbers I chose an example where no carrying was necessary. When multiplying polynomials you will NEVER have to carry.

x + 1
x – 2

We begin by multiplying the -2 on the bottom by each term on top, moving from right to left. First note that -2 times 1 is -2:

x + 1
x – 2
     –2

Next note that -2 times x is -2x:

x + 1
x – 2
–2x – 2     

Now we multiply the x on the bottom by each term on top, moving from right to left. This time as we write the answers we leave one blank space on the right:

x + 1
x – 2
–2x – 2     
x² + x               

Finally, we add:

x + 1
x – 2
–2x – 2     
x² + x               
x² – x – 2       

A “Harder” Example

One of the nicest things about this method of multiplying polynomials is that it can be used to multiply ANY two polynomials together  (not just binomials). For example, let’s multiply the trinomials x² + 2x – 1 and 2x² – x + 3 together.

    x² + 2x – 1
    2x²  –   x + 3   
3x² + 6x – 3  
–x³ – 2x²  +  x                     
2x⁴ + 4x³ – 2x²                                    
2x⁴ + 3x³  – x²  +   7x – 3                        

Summary and Further Exploration

To summarize, the algorithm I illustrated in this post is better than FOILING for the following reasons:

1. This method works for multiplying ANY two polynomials together, whereas FOIL works ONLY for binomials.
2. Everyone already essentially knows this algorithm from elementary school.
3. It is much easier to see WHY this algorithm works. I’m going to leave the “why” as an exercise.

Let me leave you a few problems to practice on your own as well as some theoretical questions.

Exercises

1. Multiply the polynomials 3x⁴ + 5x³ – x² + x – 1 and 2x³ – 3x² + x – 4.
2. Explain why the algorithm presented here works. In particular, how is the distributive property being used?
3. Show that FOIL is equivalent to the distributive property.
4. Why is FIOL more efficient than FOIL? In other words which property of the real numbers do you need to FOIL that you DO NOT need to FIOL?

If you think your friends would like this article, please share:

 

See you tomorrow…

Right Triangle Trigonometry – Part 2

Last week I began going over the fundamentals of right triangle trigonometry. I suggest that you review the material in that post before continuing on with this one. You can find that post here: Right Triangle Trigonometry – Part 1

Let’s quickly review the six basic trigonometric functions: 

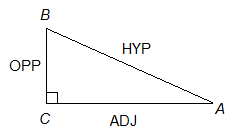
Very often in trigonometry problems on standardized tests the Pythagorean Theorem is needed to get the final answer.

The Pythagorean Theorem: If a right triangle has legs of length a and b, and a hypotenuse of length c, then c² = a² + b².

Example 3

Notes: (1) The most common Pythagorean triples are 3,4,5 and 5, 12, 13. Two others that may come up are 8, 15, 17 and 7, 24, 25.

(2) If you don’t remember the Pythagorean triple 5, 12, 13, you can use the Pythagorean Theorem:

Here we have 5² + b² = 13². Therefore 25 + b² = 169. Subtracting 25 from each side of this equation gives b² = 169 – 25 = 144. So b = 12.

(3) The equation b² = 144 would normally have solutions b = 12 and b = –12. But the length of a side of a triangle cannot be negative, so we reject –12.

More Trigonometry Practice Problems

If you are preparing for the ACT, SAT or an SAT math subject test, you may want to take a look at one of the books from the Get 800 collection of test prep books.

Right Triangle Trigonometry

Today I would like to begin talking about right triangle trigonometry. If you will be taking the ACT or one of the SAT math subject tests, and you are going for a very high score, then it is important that you understand the material covered here.

Let’s begin by focusing on angle A in the following picture: 

Note that the hypotenuse is ALWAYS the side opposite the right angle.

The other two sides of the right triangle, called the legs, depend on which angle is chosen. In this picture we chose to focus on angle A. Therefore the opposite side is BC, and the adjacent side is AC. 

Now you should simply memorize how to compute the six trig functions:

Here are a couple of tips to help you remember these:

(1) Many students find it helpful to use the word SOHCAHTOA. You can think of the letters here as representing sin, opp, hyp, cos, adj, hyp, tan, opp, adj.

(2) The three trig functions on the right are the reciprocals of the three trig functions on the left. In other words, you get them by interchanging the numerator and denominator. It’s pretty easy to remember that the reciprocal of tangent is cotangent. For the other two, just remember that the “s” goes with the “c” and the “c” goes with the “s.” In other words, the reciprocal of sine is cosecant, and the reciprocal of cosine is secant.

Note that if you are preparing for the ACT or Level 1 SAT math subject test, then it is not that important for you to know the reciprocal trig functions given in the right hand column, but it also couldn’t hurt to be somewhat familiar with them.

Example 1

To make sure you understand this, compute all six trig functions for each of the angles (except the right angle) in the triangle below.

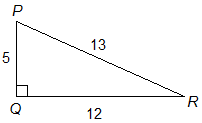
I suggest you try this yourself before looking at the answers:

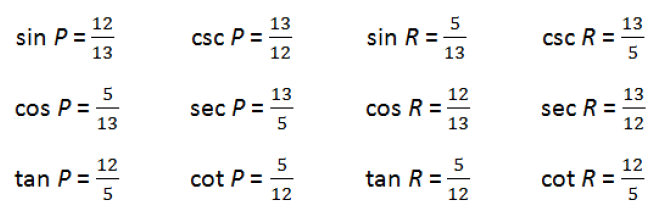
Example 2

In the right triangle pictured below, a, b, and c  and  are the lengths of its sides. What is the value of cos A ?

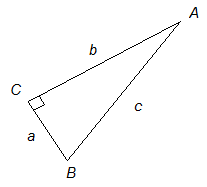
It’s quite easy if you know the rules.

Next week I will continue this thread by providing you with some more difficult examples.

More Trigonometry Practice Problems

If you are preparing for the ACT, SAT or an SAT math subject test, you may want to take a look at one of the books from the Get 800 collection of test prep books.

AP Calculus AB Exam Changes

The AP Calculus exams are going through a few small changes, and so I have been updating my AP Calculus prep books to account for these changes. The revised version of the book for the AB exam is now ready. Here is a link to the book’s Amazon page: 320 AP Calculus AB Problems

The following changes are being made to the AP Calculus AB exam beginning with the 2016-2017 academic year:

1. Multiple choice questions will have only 4 answer choices instead of 5.
2. The distribution of multiple choice questions will be modified slightly as follows: The “no calculator allowed” portion (Part A) will now consist of 30 questions (up from 28) and you will have 60 minutes (up from 55). The “calculator required” portion (Part B) will now consist of 15 questions (down from 17) and you will have 45 minutes (down from 50).
3. One new topic has been added: L’Hôpital’s rule*

* Note that there have always been problems on the AP Calculus AB exam where L’Hôpital’s rule could be used. The difference now is that problems may show up where L’Hôpital’s rule must be used. This is a very minor addition to the exam.

If you think your friends might be interested in this information, please share it with them on Facebook:

Thank you all for your continued support!

Challenging Math Questions – Solutions

Last week I gave you some challenging math questions to work on. Click the following link to see last week’s post: Some Challenging Mathematics To Raise Mathematical Maturity

Today I will provide solutions to each of those questions.

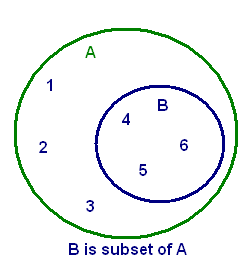
Warm-up Exercises

Recall that a set B is a subset of a set A if every element of B is an element of A. For example, if A = {1,2,3,4,5,6} and B = {4,5,6}, then B is a subset of A. Also { } is the emptyset, the unique set consisting of no elements.

1. How many subsets does { } have? List them.

{ } is a subset of every set. In particular, { } is a subset of itself. This is the only subset of { }.

So { } has 1 subset, namely { }. (Note that 1 = 2⁰)

2. How many subsets does {1} have? List them.

{1} has 2 subsets: { } and {1}. (Note that 2 = 2¹)

3. List the subsets of {1, 2}, {1, 2, 3}, and {1, 2, 3, 4}.

{1, 2} has 4 subsets. They are { } , {1}, {2}, and {1,2}. (Note that 4 = 2²)

{1, 2, 3} has 8 subsets: { } , {1}, {2}, {1,2}, {3}, {1,3}, {2,3}, and {1,2,3}. (Note that 8 = 2³)

{1, 2, 3, 4} has 16 subsets: { } , {1}, {2}, {1,2}, {3}, {1,3}, {2,3}, {1,2,3}, {4}, {1,4}, {2,4}, {1,2,4}, {3,4}, {1,3,4}, {2,3,4}, and {1,2,3, 4}. (Note that 16 = 2⁴)

4. How many subsets does the set {1, 2, 3, 4, 5, 6, 7, 8} have?

Following the pattern in the previous examples {1, 2, 3, 4, 5, 6, 7, 8} has 2⁸ = 256 subsets.

5. How many subsets does the set {1,…, n} have where n is a positive integer.

{1,…,n} has 2ⁿ subsets.

Theoretical Exercise

6. Give a proof of the result from problem 5.

Solution by Mathematical Induction: The base case is problem 1.

For the inductive step, suppose that every set A with k elements has 2^k subsets. Let B be a set with k+1 elements, and let x be any element of B. By assumption there are 2^k subsets of B that do not contain x, and 2ⁿ subsets of B that do contain x, for a total of

2^k+ 2^k = 2(2^k) = 2^k+1

subsets. By the Principle of Mathematical Induction {1,…,n} has 2ⁿ subsets for all integers n ≥ 0.

Remarks:

(i) The Principle of Mathematical Induction says that if a statement is true for n = 0, and the truth of the statement for k implies the truth for k + 1, then the statement is true for all integers n ≥ 0.

(ii) Note that the lists chosen in problems 2 and 3 emulate the proof given here.

Solution by counting: There are _nC_k subsets of {1,…, n} with k elements. So all together there are _nC₀ + _nC₁ +…+ _nC_n= (1 + 1)ⁿ = 2ⁿ subsets of {1,…, n}.

Remarks:

(i) _nC_k means the number of combinations of n things taken k at a time. In a combination order does not matter (as opposed to the permutation _nP_k where the order does matter).

_nC_k = n!/[k!(n – k)!]

We don’t actually need to do any of these computations for this problem.

(ii) Here we have used the Binomial Theorem with x = y = 1:

(x + y)ⁿ = _nC₀ xⁿy⁰ + _nC₁ x^n-1y¹ +…+ _nC_n-1 x¹y^n-1 + _nC_n x⁰yⁿ

(1 + 1)ⁿ = _nC₀ 1ⁿ1⁰ + _nC₁ 1^n-11¹ +…+ _nC_n-1 1¹1^n-1 + _nC_n 1⁰1ⁿ

2ⁿ = _nC₀  + _nC₁ +…+ _nC_n-1 + _nC_n

Advanced Exercises

Recall that a set is selfish if the number of elements it has is in the set. For example, X₁₀ = {1,2,3,4,5,6,7,8,9,10} is selfish because it has 10 elements, and 10 is in the set. A selfish set is minimal if none of its proper subsets is also selfish. For example, the set X₁₀ is not a minimal selfish set because {1} is a selfish subset. Let  X_n = {1,…,n}.

7. How many selfish subsets does X_n have where n is a positive integer?

Let’s start with some simple examples.

X₁ = {1} has 1 selfish subset, namely {1} itself.

The selfish subsets of X₂ = {1,2} are {1} and {1,2}, so that X₂ has 2 selfish subsets.

The selfish subsets of X₃ = {1,2,3} are {1}, {1,2}, {2,3}, and {1,2,3}, so that X₃ has 4 selfish subsets.

The selfish subsets of X₄ = {1,2,3,4} are {1}, {1,2}, {2,3}, {1,2,3}, {2,4}, {1,3,4}, {2,3,4} and {1,2,3,4}, so that X₄ has 8 selfish subsets.

In general, it looks like X_n has 2^n-1 selfish subsets.

To see this, note that there are _n-1C_k-1 selfish subsets of {1,…,n} with k elements (we must choose k, and then we choose k – 1 elements from the remaining n – 1 elements). So all together there are

_n-1C₀ + _n-1C₁ +…+ _n-1C_n-1 = (1 + 1)^n-1 = 2^n-1

selfish subsets of {1,…,n}.

8. List the minimal selfish subsets of X_n for n = 1, 2, 3, 4, 5, and 6.

X₁ has 1 minimal selfish subset, namely {1}.

X₂ has 1 minimal selfish subsets, namely {1}. (Note that {1,2} is selfish, but not minimal because {1} is a selfish subset.)

X₃ has 2 minimal selfish subsets, namely { 1} and {2,3}.

X₄ has 3 minimal selfish subsets, namely {1}, {2,3}, and {2,4}.

X₅ has 5 minimal selfish subsets. They are {1}, {2,3}, {2,4}, {2,5}, and {3,4,5}.

X₆ has 8 minimal selfish subsets. They are {1}, {2,3}, {2,4}, {2,5}, {3,4,5}, {2,6}, {3,4,6}, and {3,5,6}.

9. How many minimal selfish subsets does X₁₀ have?

Following the pattern, it looks like X₇ has 8 + 5 = 13 minimal selfish subsets, X₈ has 13 + 8 = 21, X₉ has 21 + 13 = 34, and X₁₀ has 34 + 21 = 55 minimal selfish subsets.

10. In terms of n, how many minimal selfish subsets does the set X_n have?

X_n has f_n minimal selfish subsets where f_n is the nth term of the Fibonacci sequence.

Remark: The Fibonacci sequence is the sequence

f_n = f_n-1 + f_n-2,  f₁ = f₂ = 1.

The first few terms of the Fibonacci sequence are

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

11. Give a proof of the result from problem 10.

We will prove this by the Principle of Strong Induction on n, with the base case of n = 1 and n = 2 already complete. Assume that k > 2 and that X_r has f_r minimal selfish subsets for each r < k. Each minimal selfish subset of X_k-1 is a minimal selfish subset of X_k, and if A is a minimal selfish subset of X_k-2, then the set A’ formed by adding 1 to each element of A, and throwing in k, is a minimal selfish subset of X_k. This yields f_k-1 + f_k-2 = f_k minimal selfish subsets of X_k. Conversely, note that if a minimal selfish subset of X_k does not contain k, then it is a minimal selfish subset of X_k-1, and if a minimal selfish subset of X_k does contain k, then if we delete k and subtract 1 from each of the remaining elements we get a minimal selfish subset of X_k-2. Thus there are exactly  f_k minimal selfish subsets of X_k.

Remark: The Principle of Strong Induction says that if a statement is true for n = 0 (or more generally n = m), and the truth of the statement for all r < k implies the truth for k, then the statement is true for all integers n ≥ 0 (or more generally n ≥ m).

If you liked this article, please share it with your Facebook friends:

If you would like to begin learning more advanced mathematics, check out my math books Pure Mathematics for Beginners, Set Theory for Beginners, and Topology for Beginners. These books contain no prerequisites and are perfect for anyone just starting out in theoretical math. You can get them all for one low price by clicking on the image below.

Challenging Mathematics to Raise Mathematical Maturity

I like to define mathematical maturity as “one’s ability to analyze, understand, and communicate mathematics.” Students with higher levels of mathematical maturity are more likely to perform well on standardized math tests. For more information about mathematical maturity, click on the following link: Mathematical Maturity

Challenging Mathematics

Today I would like to challenge you a bit while helping you take some steps toward increasing your level of mathematical maturity by presenting you with some more difficult mathematics.  Solutions to the questions below will be provided in tomorrow’s blog post, but please post your solutions or partial solutions in the comments below.

Basic Definition

The first few questions will use the following definition:  B is a subset of a set A if every element of B is an element of A.

For example, if A = {1,2,3,4,5,6} and B = {4,5,6}, then B is a subset of A.

As another example, if C = {a,b}, then all of the subsets of C are { }, {a}, {b}, and {a,b} (here { } is the emptyset, the unique set consisting of no elements).

Warm-up Exercises

1. How many subsets does { } have? List them.
2. How many subsets does {1} have? List them.
3. List the subsets of {1,2}, {1,2,3}, and {1,2,3,4}.
4. How many subsets does the set {1,2,3,4,5,6,7,8} have?
5. How many subsets does the set {1,…,n} have where n is a positive integer.

Theoretical Exercise

6. Give a proof of the result from problem 5.

There are several methods that can be used for number 6. I personally prefer to use Mathematical Induction. Those of you that know this method should give it a try. More information can be found at this Wikipedia page: Mathematical Induction

There are several other methods that can be used as well. Please post your attempts at this problem in the comments.

Now let’s take a look at some more advanced concepts.

Advanced Definitions

Define a set to be selfish if the number of elements it has is in the set.

For example, X₁₀ = {1,2,3,4,5,6,7,8,9,10} is selfish because it has 10 elements, and 10 is in the set.

A selfish set is minimal if none of its proper subsets is also selfish.

For example, the set X₁₀ is not a minimal selfish set because {1} is a selfish subset.

Let  X_n = {1,…,n}.

Advanced Exercises

7. How many selfish subsets does X_n have where n is a positive integer?
8. List the minimal selfish subsets of X_n for n = 1, 2, 3, 4, 5, and 6.
9. How many minimal selfish subsets does X₁₀ have?
10. In terms of n, how many minimal selfish subsets does the set X_n have?
11. Give a proof of the result from problem 10.

If you liked this article, please share it with your Facebook friends:

Solutions will be provided tomorrow.

If you would like to begin learning more advanced mathematics, check out my math books Pure Mathematics for Beginners, Set Theory for Beginners, and Topology for Beginners. These books contain no prerequisites and are perfect for anyone just starting out in theoretical math. You can get them all for one low price by clicking on the image below.

Hard Problem Solving Question

Last week I gave you a Level 5 Problem Solving question for the revised SAT to try. Today I will provide a solution for this problem. If you have not yet attempted the problem go back and take a look at it first so you can try it on your own. Here is the link: Hard Problem Solving Question for the Revised SAT

Level 5 – Problem Solving

Here is the problem once again followed by a solution:

John, a United States resident, is on vacation in Spain and is trying to decide if he should use his own credit card from the U.S., or to purchase a prepaid credit card for 500 euros in Spain.

The bank that issues John’s U.S. credit card converts all purchase prices at the foreign exchange rate for that day, and an additional fee of 6% of the converted cost is applied before the bank posts the charge.

If John decides to purchase the prepaid card, he can use this card spending dollars at the exchange rate for that day with no fee, but he loses any money left unspent on the card.

Suppose that John does decide to buy the prepaid card. What is the least number of the 500 euros John must spend for the prepaid card to have been the cheaper option? Round your answer to the nearest whole number of euros.

Solution: If we let d be the cost of the 500 euro card in dollars, and we let e be John’s total purchases on the prepaid card in euros, we need

d < 1.06(d/500)e.

We can divide each side of this inequality by d to get 1 < e(1.06/500), and then multiply each side of this last equation by 500/1.06 to get 500/1.06 < e, or equivalently e > 471.698 .

So the least number of the 500 euros John must spend is 472.

For an even more detailed  solution to this problem check out  New SAT Math Problems arranged by Topic and Difficulty Level.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out New SAT Math Problems arranged by Topic and Difficulty Level. Click on the picture below for more information about this book.

If you think your friends would like to try this problem, please share:

Speak to you soon!

Hard Problem Solving Question

Today I would like to provide an example of a hard “problem solving” question that could show up on the revised SAT. You can use your calculator for this one.

Level 5 – Problem Solving

John, a United States resident, is on vacation in Spain and is trying to decide if he should use his own credit card from the U.S., or to purchase a prepaid credit card for 500 euros in Spain.

The bank that issues John’s U.S. credit card converts all purchase prices at the foreign exchange rate for that day, and an additional fee of 6% of the converted cost is applied before the bank posts the charge.

If John decides to purchase the prepaid card, he can use this card spending dollars at the exchange rate for that day with no fee, but he loses any money left unspent on the card.

Suppose that John does decide to buy the prepaid card. What is the least number of the 500 euros John must spend for the prepaid card to have been the cheaper option? Round your answer to the nearest whole number of euros.

Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve the problem. I will post a solution to this problem tomorrow.

More Hard SAT Math Practice Problems

For many more hard SAT math problems like these, each with several fully explained solutions, check out New SAT Math Problems arranged by Topic and Difficulty Level. Click on the picture below for more information about this book.

 

If you think your friends would like to try this problem, please share:

Speak to you soon!

The Arithmetic Sequence Formula

Welcome back. Today I would like to conclude our discussion on arithmetic sequences that we began a few days ago. I recommend that you reread the first two posts on this topic before you move on to this one. Here are the links:

Arithmetic Sequences – Part One

Arithmetic Sequences – Part Two

Recall that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to give a very formal method for solving problems involving arithmetic sequences. Note that it is not necessary to learn this material in order to answer these types of questions on the ACT or SAT math subject tests, but every now and then the method given here gives a quicker way to solve a problem.

The arithmetic sequence formula

More advanced students may already know the arithmetic sequence formula:

In this formula a_n is the nth term of the sequence. For example, a₁ is the first term of the sequence.

Example 1

In the arithmetic sequence 20, 15, 10, 5, 0, -5, -10,… we have a₁ = 20 and d = -5. Therefore we have

So for example, the 50th term of this arithmetic sequence is

Let’s revisit the second example from last week, but this time we will give a solution using the arithmetic sequence formula.

Example 2

Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: Substituting 5 in for n and 33 in for a_n into the arithmetic sequence formula gives us

33 = a₁ + 4d.

Similarly, substituting 9 in for n and 97 in for a_n into the arithmetic sequence formula gives us

 97 = a₁ + 8d.

So we solve the following system of equations to find d.

97 = a₁ + 8d
33 = a₁ + 4d
64 =        4d

The last equation comes from subtraction. We now divide each side of this last equation by 4 to get

d = 16.

Finally, we add 16 to 97 three times to get 97 + 16(3) = 145.

Note that this solution is definitely more tedious than the previous solution from last week’s post. I usually prefer identifying arithmetic sequences with linear equations.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends: