500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Arithmetic Sequences and Linear Equations

Hello again. Today I would like to continue our discussion on arithmetic sequences from yesterday. I recommend that you reread yesterday’s post before you move on to this one. Here is the link: Arithmetic Sequences

Recall from last week that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to focus on the relationship between arithmetic sequences and linear equations.

Arithmetic sequences and linear equations

Recall the formula for the slope of a line:

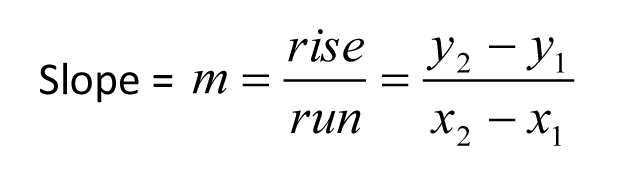
There is a natural correspondence between arithmetic sequences and linear equations. Each term of an arithmetic sequence can be naturally identified with a point on the corresponding line. Let’s go back to our first example of an arithmetic sequence from last week:

Example 1

1, 4, 7, 10, 13, 16,…

We can identify terms of the sequence with points on a line where the x-coordinate is the term number and the y-coordinate is the term itself.

(1,1), (2,4), (3,7), (4,10), (5,13), (6,16),…

These points all lie on the same line, and we can compute the slope of this line by using any two of these points. For example, let’s use the points (2,4) and (6,16).

We have

m = (16 – 4)/(6 – 2) = 12/4 = 3

Do you recognize this number? That’s right! It’s the common difference of the sequence.

The identification of arithmetic sequences with linear equations gives us a nice method for finding the common difference of an arithmetic sequence as long as we know any 2 terms of the sequence.

Let’s try another example.

Example 2

Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: We identify the two given terms with the points (5,33) and (9,97). The common difference is then

d = (97 – 33)(9 – 5) = 64/4 = 16 

The twelfth term is then  97 + 16(3) = 145.

The information already covered in this post and the last is all you really need to know, but for completeness, tomorrow I’m going to talk about the arithmetic sequence formula.

More Problems Involving Arithmetic Sequences

If you are preparing for a standardized test, take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

320 SAT Math Subject Test Problems – Huge Sale! 

Just $5.54 On Amazon

Today I would like to announce a huge sale on my book 320 SAT Math Subject Test Problems arranged by Topic and Difficulty Level for the Level 2 test.

The paperback is now on sale on Amazon for only $5.54.

This sale may last for only a few hours, and once the sale ends the price will go up to $34.99. Amazon will automatically raise the price once a predetermined number of copies has been sold. If you want to take advantage of the sale price I strongly recommend you purchase the book now.

Click the following link to get to the book’s Amazon page:

320 SAT Math Subject Test Problems – Level 2

As an extra incentive to buy this book from Amazon I want to offer you an additional book for FREE as a downloadable PDF file. You can choose ANY of my other books. So if you would like a different book, go ahead and purchase this one, forward me your Amazon confirmation email and let me know which of my books you would like for free. You will be provided with a link to download your additional free book. This offer is available until midnight of May 31, 2016.

You can forward your Amazon confirmation to

steve@SATPrepGet800.com

Take a look at my product page to see all of my books: Get 800 Product Page

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

Thank you all for your continued support!

Arithmetic Sequences

Hello everyone. Today I would like to talk about arithmetic sequences. Questions involving arithmetic sequences appear on the ACT, GRE and SAT math subject tests.  Here is an example of an arithmetic sequence.

Example 1

1, 4, 7, 10, 13, 16,…

Note that the first term of this sequence is 1, the second term of this sequence is 4, and so on.

So what makes this sequence arithmetic?

Well notice that to get from 1 to 4 we need to add 3. To get from 4 to 7 we also add 3. To get from 7 to 10 we also add 3. In other words, the sequence is arithmetic because we always add the same number to get from any term to the next term. This special number is called the common difference of the arithmetic sequence.

So why is this number called the common difference? Well another way to compute the common difference is to note that when we subtract any term from the next term we always get the same number, in this case that number is d = 3.

In other words we have 4 – 1 = 3, 7 – 4 = 3, and so on.

An arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence.

Let’s try a simple example.

Example 2

The second term of an arithmetic sequence is 15 and the third term is 10. What is the first term?

A.  –15
B.  –10
C.    1/15
D.    10
E.    20

Solution: Moving backwards, to get from the third term to the second term we add 5. Therefore we add 5 more to get to the first term. So the first term is

15 + 5 = 20.

This is choice E.

Note that in an arithmetic sequence, you always add (or subtract) the same number to get from one term to the next. This can be done by moving forwards or backwards through the sequence.

Note also that the common difference of this sequence is  d = 10 – 15 = –5.

Many students might mistakenly say that the common difference is 5.

This particular problem was pretty simple, so we were able to solve it just by “counting.” In other words we didn’t really have to worry about the formalities of whether the common difference was positive or negative. But in harder questions we might need to be more careful.

Alternate solution: Note that the terms of the sequence are getting smaller so that the first term must be larger than 15. So the answer must be choice E.

In my next post we will learn a special technique that makes many seemingly difficult problems involving arithmetic sequences very easy to solve. Check it out here: Arithmetic Sequences and Linear Equations

More Practice with Arithmetic Sequences

If you are preparing for a standardized test, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

 

Greatest Common Divisor (GCD)

and Least Common Multiple (LCM)

Hi everyone. How are we doing today?

Today I would like to help you solve math problems that involve finding the greatest common divisor and least common multiple of a set of positive integers. This can be extremely useful for standardized tests like the ACT and GRE. But before I even get to today’s post, I would like to go back to yesterday’s post on Prime Factorizations where I asked you to draw a factor tree for the number 6137. You can find that post here: Integers, Prime Numbers, and Prime Factorizations

Solution to Last Week’s Question

Let’s compare our drawings.

As I mentioned last week, it’s not artistic merit I am looking for, but rather that the numbers in your ‘tree’ are correct.

Let’s start by taking the square root of 6137. Punching that into your calculator, we see that we get about 78.3. So using the tip that I gave to you last week, we will divide 6137 by the prime numbers less than 78.3.

The primes less than 78.3 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 and 73.

The good news is that we do not need to divide by all of these numbers to ind our factors – let me explain: Dividing by 2, 3, 5, 7, 11, and 13 do not produce integers, but 6137/17 = 361.

Now, the square root of 361 is exactly 19 (this is easily checked in your calculator). So 361 = (19)(19) = 19².

So 6137 = 17 · 19².

Here is my factor tree:

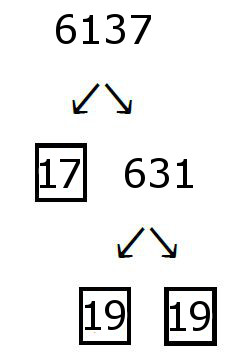
How does your tree look compared to mine? Get in touch if you have any questions regarding this…

GCD and LCM

Now for the main part of the post…

The greatest common divisor (gcd) of a set of positive integers is the largest positive integer that each integer in the set is divisible by.

The least common multiple (lcm) of a set of positive integers is the smallest positive integer that is divisible by each integer in the set.

Example 1

Let’s find the gcd and lcm of 9 and 15.

There are a few ways we can do this.

First method: The factors of 9 are 1, 3 and 9. The factors of 15 are 1, 3, 5 and 15. So the common factors of 9 and 15 are 1 and 3. Therefore we see that gcd (9,15) = 3.

The multiples of 9 are 9, 18, 27, 36, 45, 54, 63,… and the multiples of 15 are 15, 30, 45,.. We can stop at 45 because 45 is also a multiple of 9. Therefore we see that lcm (9,15) = 45.

Second method: We first find the prime factorizations of 9 and 15. We see that 9 = 3² and 15 = 3 · 5. To find the gcd we multiply together the smallest powers of each prime from both factorizations, and for the lcm we multiply the highest powers of each prime. So we have gcd (9,15) = 3 and we have lcm (9,15) = 3² · 5 = 45.

Now take note – If you have trouble seeing where the gcd and lcm are coming from here, it may be helpful to insert the “missing” primes. In this case, 5 is missing from the factorization of 9. So it might help you if you write 9 = 3² · 5º. Now we can think of the gcd as 3¹ · 5º = 3.

Third method: Your calculator can actually do this for you (not on the GRE though)! On your TI-84 calculator press MATH, scroll right to NUM. For the gcd press 9, type 9,15 and press ENTER. You will see an output of 3. For the lcm press 8, type 9,15 and press ENTER for an output of 45.

Example 2

Let’s try another example: Find the gcd and lcm of 100 and 270.

The prime factorizations of 100 and 270 are 100 = 2² · 5² and 270 = 2 · 3³ · 5. So gcd (100,270) = 2 · 5 = 10 and lcm (100,270) = 2² · 3³ · 5² = 2700.

If we were to insert the ‘missing’ primes in the prime factorization of 100 we would get 100 = 2² · 3⁰ · 5². So we can think of the gcd as 2¹ · 30 · 5¹ = 10.

Example 3

Okay, now let’s try an ACT math question…

What is the least positive integer divisible by the integers 3, 7 and 14?

A. 168
B. 126
C. 84
D. 42
E. 28

Calculator method: The question is actually asking for the least common multiple of 3, 7 and 14. Your calculator can only do two at a time. So first compute lcm (3,7) = 21, and then compute lcm (21,14) = 42, choice D.

Simple!

Solution by Starting with choice E: Begin by looking at choice E since it is the smallest. 28/3 comes to approximately 9.33 in our calculator. Since this is not an integer, 28 is not divisible by 3. We can therefore eliminate choice E. We next try choice D.

42/3 = 14, 42/7 = 6, 42/14 = 3

Since these are all integers, the answer is choice D.

For more information on this strategy see the following blog post: Starting With Choice C – A Basic SAT Math Strategy.

Example 4

Now here is a much more difficult example for us to try together:

The integer k is equal to m² for some integer m. If k is divisible by 6 and 40, what is the smallest possible positive value of k?

Did you realize that we are looking for the smallest perfect square that is divisible by the least common multiple of 6 and 40? Let’s find some prime factorizations: 6 = 2 · 3, and 40 = 2³ ·5. So lcm (6,40) = 2³ · 3 · 5. The least perfect square divisible by this number is 2⁴ · 3² · 5² = 3600.

It’s not too hard when you know how to compute the lcm.

This was quite a long blog post, but I hope you have received some good value from it.

Click on the picture below for more information about the Get 800 collection of test prep books.

Integers, Prime Numbers And Prime Factorizations

I would like to begin today with a few simple definitions of terms that appear in number theory problems on the ACT , GRE and SAT math subject tests.

Definitions

The integers are the counting numbers together with their negatives.

…,-4, -3, -2, -1, 0, 1, 2, 3, 4,…

The positive integers consist of the positive numbers from the above list.

1, 2, 3, 4,…

Next we have prime numbers.

A prime number is a positive integer that has exactly two factors (1 and itself). Here is a list of the first few primes:

2, 3, 5, 7, 11, 13, 17, 19, 23,…

Note that 1 is not prime. It has only one factor.

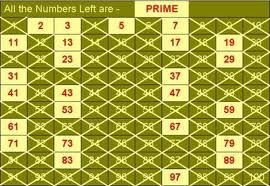
A little trick:

Here is a quick trick for determining if a large number is prime: take the square root of the integer and check if the integer is divisible by each prime up to this square root. If not, the number is prime.

For example let’s try to figure out if 3001 is a prime number. Note that when we take the square root of 3001 in our calculator we get approximately 54.8. Now with our calculators we divide 3001 by 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, and 53 (all the prime numbers below 54.8). Since none of these are integers, 3001 is prime.

The Fundamental Theorem of Arithmetic

The fundamental theorem of arithmetic says “every integer greater than 1 can be written “uniquely” as a product of primes.”

The word “uniquely” is written in quotes because prime factorizations are only unique if we agree to write the primes in increasing order.

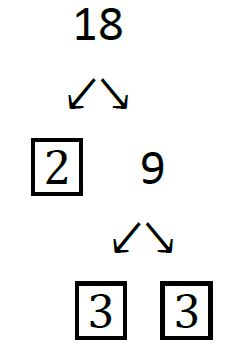
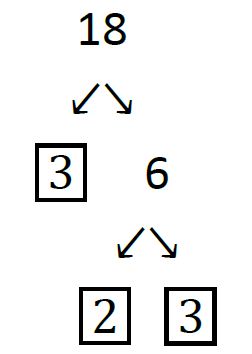
For example, 6 can be written as 2 · 3 or as 3 · 2. But these two factorizations are the same except that we changed the order of the factors. To make things as simple as possible we always agree to use the canonical representation. The word “canonical” is just a fancy name for “natural,” and the most natural way to write a prime factorization is in increasing order of primes. So the canonical representation of 6 is 2 · 3. As another example, the canonical representation of 18 is 2 · 3 · 3. We can tidy this up a bit by rewriting 3 · 3 as 3². So the canonical representation of 18 is 2 · 3². If you are new to factoring, you may find it helpful to draw a factor tree. For example here is a factor tree for 18:

To draw this tree we started by writing 18 as the product 2 · 9. We put a box around 2 because 2 is prime, and does not need to be factored anymore. We then proceeded to factor 9 as 3 · 3. We put a box around each 3 because 3 is prime. We now see that we are done, and the prime factorization can be found by multiplying all of the boxed numbers together. Remember that we will usually want the canonical representation, so write the final product in increasing order of primes.

By the Fundamental Theorem of Arithmetic above it does not matter how we factor the number – we will always get the same canonical form. For example, here is a different factor tree for 18:

For practice, why don’t you try to draw a factor tree for 6137? Note that this is much more challenging than any number you will have to factor on a standardized test. I’ll have the solution for you tomorrow, so we can compare notes then. Remember, I am not looking for artistic merit – just make your factors clear in your drawing.

How many prime numbers are there?

This is going off on a bit of a tangent, but there are an infinite number of prime numbers. This was first proved by the ancient Greek mathematician Euclid.

Interestingly, the largest prime number found so far is  2^57,885,161 – 1. That’s a number with 17 million digits! I dare you to find the next one greater than that.

In the meantime, if you want to learn mathematical strategies to efficiently answer math questions on standardized tests, I would suggest that you take a look at the Get 800 collection of test prep books. Click on the picture below for more information about these books.

 

Turn Wrong Answers Into Right Answers

On Standardized Tests

Today I want to discuss a common mistake that students make which leads to bad preparation.  The type of mistake I am about describe is especially common during preparation for standardized tests such as the ACT, SAT and GRE.

Although many problems on standardized tests can be very difficult to solve, it is usually not very hard to understand the solutions. After getting a problem wrong, a good student will go over the solution until they understand it completely. Very often, however, the same student will misinterpret understanding the solution as being able to reproduce the solution on their own.

If after a student gets a question wrong I explain the correct way to do it and they understand my explanation, then more than likely if I ask them to solve the question 5 minutes later they will be able to do so. But it is important to realize that this does not mean that they will be able to solve a similar question (or even the exact same question) two months later during their SAT.

Understanding a solution and being able to reproduce it using short term memory does not necessarily lead to long term retention.

So what is the answer? How does a student make sure that they do not make the same mistake on their actual exam that they had made during their preparation?

The answer is quite simple.

During preparation, anytime you get a question wrong mark it off. You should have a special mark that is easy to see and recognize. Students of mine use stars, spirals or even sad faces.

Yes, the marks above were created in MS Paint! But I’m sure, you get the idea…

It is very important to mark off every single question you have gotten wrong regardless of the reason. Even if the only reason you got it wrong was because you accidentally hit a wrong button in your calculator, or even if you got it wrong because you just misread one of the numbers in the problem – mark it off anyway! It is very easy to say “oh that was just a silly mistake – I know how to do this,” and then to never look at that problem again. This is a huge mistake. Let me repeat this one more time. Mark off EVERY question you get wrong. Every question! Not just the ones you do not understand. EVERY SINGLE ONE!

You must reattempt each question you get wrong at least four days later. Do not reattempt the problem the next day, or the day after that. If you wait only one or two days you may be getting the problem correct for the wrong reason. The question is too fresh in your mind. You need time to forget how you solved it. This way you can be sure that you understand how to solve the problem, as opposed to simply recalling the solution.

If you get the problem correct you can “unmark” it and remove it from the list of problems you need to redo. If you get it wrong again, then leave it marked off and reattempt it again at least four days later. You need to keep reattempting each problem you get wrong with at least four days between attempts. You should only stop reattempting a problem once you get it completely correct on your own without recalling exactly how the problem was solved. Only then can you know for certain that you have internalized the technique necessary to solve that problem.

If you follow the advice I have given here, then every time you get a problem right that you had previously gotten wrong, you will be one step closer to a perfect score on the SAT, ACT, GRE, or whichever exam you are preparing for.

I want you to treat this message in the same way as I recommend you treat a question you answer incorrectly. Come back to this article in four days time. Reread it. Internalize it. I am certain you will benefit from the information given here if you make it a part of your long term memory..

And if if you would like lots of practice problems I suggest you take a look at the Get 800 collection of test prep books.  Click on the image below for more information about these books.

How Many Questions Should You Be Attempting

In Each GRE Math Section?

The last couple of days I explained why most students should not be attempting every math question on the SAT and ACT, and I gave tables displaying how many questions they should be answering based upon their current PSAT/SAT or ACT math score. To see that information, follow these links:

SAT        ACT

Today I will give you similar information for the GRE. As for the SAT and ACT, many students can increase their GRE math score by decreasing the number of questions they attempt to solve. Your goal when taking the GRE should be to maximize your score, and not to solve every single problem. If you are going for a perfect 140, then of course you will need to solve every problem, but for most of us, we won’t have to do that.

The following chart gives a general guideline for how many questions you should be attempting in each math section. The leftmost column is your latest score on an official practice test. The middle column shows how many questions you should answer in each math section if you are taking the computer based test. The rightmost column shows how many questions you should answer in each math section if you are taking the paper based test.

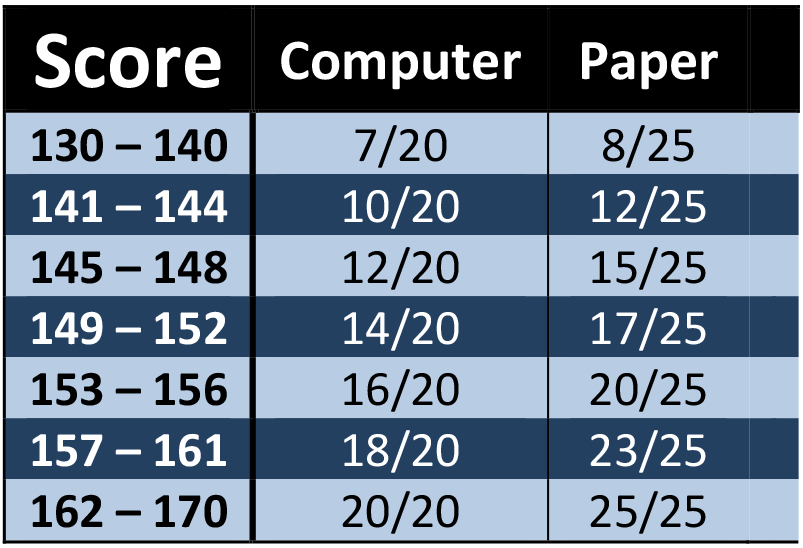
For example, a student with a current score of 155 on the computer based test should attempt about 16 questions in each math section. This is just a general guideline. Of course it can be fine-tuned. As a simple example, if you are particularly strong at Arithmetic problems, but very weak at Geometry problems, then you may want to try every Arithmetic problem no matter where it appears, and you may want to reduce the number of Geometry problems you attempt.

Remember that there is no guessing penalty on the GRE, so you should not leave any questions blank. This does not mean you should attempt every question. It means that if you are running out of time make sure you fill in answers for all the questions you did not have time to attempt.

For example, if you are currently scoring a 151 on the computer based test, then it is possible you will only be attempting about 14 questions in each section. Therefore, when you are running out of time you should fill in answers for the remaining 6 problems. If you happen to get a chance to attempt some of them, you can always change your answer. But make sure those answers are filled in before the test ends!

If you are currently preparing for the GRE, you may want to take a look at the 320 GRE Math Problems.

How Many Questions Should You Be Attempting

In Each ACT Math Section?

Yesterday I explained why most students should not be attempting every math question on the SAT, and I gave a table displaying how many questions they should be answering based upon their current PSAT or SAT math score. To see that information, follow this link:

How Many Questions Should You Be Attempting In Each SAT Math Section

Today I will give you similar information for the ACT. As for the SAT, many students can increase their ACT math score by decreasing the number of questions they attempt to solve. Your goal when taking the ACT should be to maximize your score, and not to solve every single problem. If you are going for a perfect 36, then of course you will need to solve every problem, but for most of us, we won’t have to do that.

There is only one 60 question math section on the ACT. You should first make sure that you know what you got on your last official ACT practice test or actual ACT (whichever you took last). What follows is a general goal you should go for when taking the exam.

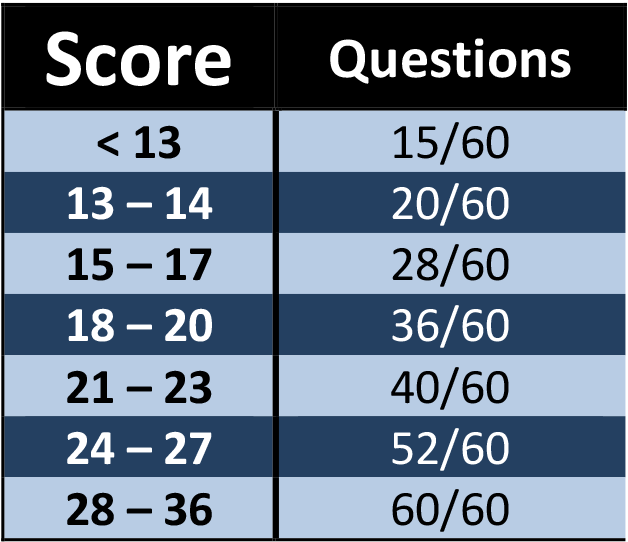
For example, a student with a current score of 22 should attempt 40 of the 60 questions. This could be the first 40 questions, but it is okay to skip a few here and there and try some that come a little later instead.

This is just a general guideline. Of course it can be fine tuned. As a simple example, if you are particularly strong at algebra problems, but very weak at geometry problems, then you may want to try every algebra problem no matter where it appears, and you may want to reduce the number of geometry problems you attempt.

Important note: There is no guessing penalty on the ACT. You should therefore fill in an answer for every question, even those questions that you do not attempt to solve. Simply take guesses for those last questions before time is up.

If you are currently preparing for the ACT, you may want to take a look at my series of ACT math books.

How Many Questions Should You Be Attempting

In Each SAT Math Section?

Students often ask me if there is any way they will ever be able to get through all of the SAT math questions in the given amount of time. In response, I always explain they are asking the wrong question. For most students, worrying about getting to the end of the test will not improve your score. Of course, if you are shooting for an 800, it goes without saying that you need to attempt and correctly solve every problem on SAT day (although there are rare instances, once every few years, in which there is an SAT where you can miss one math problem and still score an 800).

For most students, the problem is that they are already attempting too many questions. This advice might sound strange at first because students have been conditioned not to leave questions blank on tests. But the fact is, on a standardized test, students will usually increase their score by reducing the number of questions that they attempt.

First, let’s have a quick overview of the math section on the SAT: There are two math sections on the SAT – one where a calculator is allowed and one where a calculator is not allowed. The calculator section has 30 multiple choice (mc) questions and 8 free response (grid in) questions. The non-calculator section has 15 multiple choice (mc) questions and 5 free response (grid in) questions.

You should first make sure that you know what you got on your last SAT practice test, actual SAT, or actual PSAT (whichever you took last). What follows is a general goal you should go for when taking the exam.

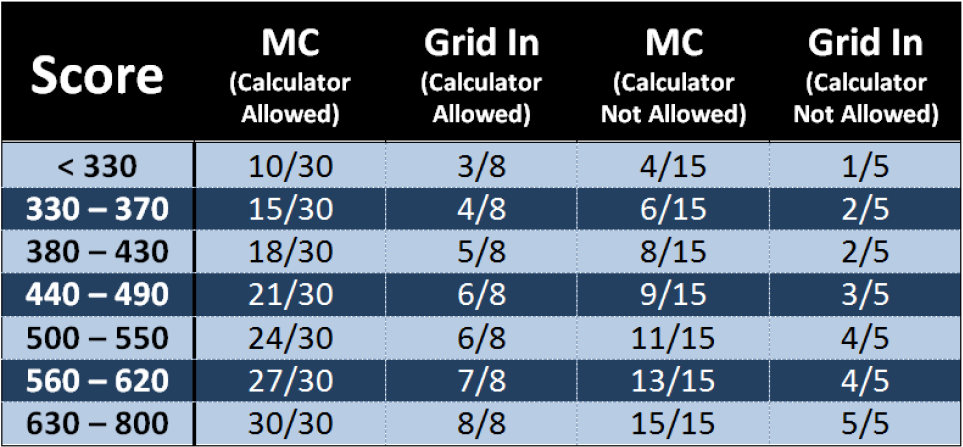
For example, a student with a current score of 450 should attempt the first 21 multiple choice questions and 6 grid ins from the section where a calculator is allowed, and the first 9 multiple choice questions and 3 grid ins from the section where a calculator is not allowed.

This is just a general guideline. Of course it can be fine tuned. As a simple example, if you are particularly strong at algebra problems, but very weak at geometry problems, then you may want to try every algebra problem no matter where it appears, and you may want to reduce the number of geometry problems you attempt.

Important note: There is no guessing penalty on the SAT. You should therefore fill in an answer for every question, even those questions that you do not attempt to solve. Simply take guesses for those last questions before time is up.

If you are currently preparing for the SAT, you may want to take a look at the 28 SAT Math Lessons series.

SHSAT Verbal Prep Book – Just $4.54 on Amazon

Today I would like to announce the release of SHSAT Verbal Prep Book to Improve Your Score in Two Months. 

The paperback is now on sale on Amazon for only $4.54. This sale may run for just a few hours (until 12 PM), and once the sale ends the price will go up to $34.99. If you want to take advantage of the sale price I strongly recommend you purchase the book right away.

Click the following link to get to the book’s Amazon page: SHSAT Verbal Prep Book

As an additional incentive to purchase this book today, I will also give you another book for FREE as a downloadable PDF file. You can choose ANY of my other books. So if you would like a different book, go ahead and purchase this one (as soon as it is available), forward me your Amazon confirmation email and let me know which of my books you would like for free. You will be provided with a link to download your additional free book. This offer is available until the end of today (May 23, 2016).

Take a look at my product page to see all of my books: Get 800 Product Page

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

Thank you all for your continued support!