500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

When to Use the Most Common Math Strategies

There are three very basic math strategies for standardized tests that every high school student should know: Plugging In Answer Choices, Taking Guesses, and Picking Numbers. Take a look at these links before you continue with this message, as the information below will make more sense after a quick review of these strategies.

Sometimes students get confused about when to use which of these strategies. Although there are no definite rules I can give you that will work 100 percent of the time, today I will provide you with some general guidelines.

Plugging In

Let’s begin with the strategy of plugging in answer choices:

This strategy can only be used for multiple choice questions. You simply plug each answer choice into the question until you find the one works. It is always best to start with choice C as your first attempt, unless there is a specific reason not to (on the new SAT you can start with choice B or C, as there are now just four choices). An example of such a reason would be that the word “least” appears in the problem. In this case start with the smallest answer choice (which will usually be choice A or E). Similarly, if the word greatest appears in the problem, start with the largest answer choice.

Plugging in can be used on problems from every topic and difficulty level. It’s often a great way to avoid having to perform messy algebra.

This strategy is most useful when the last part of the question says “What is_____” where the blank contains a single quantity.

Here are some examples:

(1) What is the value of x?
(2) What is the length of the original rectangle?
(3) What is the second number in the list?
(4) Which of the following is a perfect cube?
(5) What is the least such value of x?

For the first four of these examples you would start with choice C. For the fifth example you should start with the smallest answer choice.

This strategy is generally NOT useful when you are asked to find a more complicated expression. For example, do not try to plug in answer choices if the question ends with

“What is the value of x + y?”

In this case you will probably want to use the strategy of “Taking a guess,” or possibly “Picking numbers.”

During your SAT math practice sessions, you should try to apply this strategy on every multiple choice question. The more you attempt to use it, the easier it will be to detect when it can be applied.

Here is a straightforward example of a Level 1 Number Theory problem where “starting with choice C” is a useful strategy.

Three consecutive integers are listed in increasing order. If their sum is 138, what is the second integer in the list?

A. 45
B. 46
C. 47
D. 48
E. 49

I suggest you try to solve this problem in 3 ways:

• by starting with choice C
• algebraically
• using the fact that in a list of consecutive integers, the arithmetic mean is equal to the median.

And here is a Level 4 Geometry problem where this strategy is effective:

The sum of the areas of two squares is 85. If the sides of both squares have integer lengths, what is the least possible value for the length of a side of the smaller square?

A. 1
B. 2
C. 6
D. 7
E. 9

You should solve this problem by starting with choice A.

There are more examples in my original blog post titled Plugging in Answer Choices.

Taking Guesses

Next let’s talk about the strategy of taking a guess:

This strategy is similar to plugging in, except with this one you are not using the answer choices. The reason you are not using the answer choices is either because it is a grid in problem (so there are no answer choices), or the question is asking for a more complicated expression such as “the value of x + y,” or “the perimeter of a geometric figure.” In the first case you may want to take a guess for x or y, and in the second case you may want to take a guess for the width of a side of the figure. For examples of applying this strategy see my original blog post titled Taking A Guess. For a more difficult example, see my blog post titled Taking a Guess – A More Difficult Example.

Picking Numbers

And finally, let’s talk about the strategy of picking numbers:

This strategy is applied by choosing specific values for the unknown quantities in the problem. A new problem is formed that is easier to solve. After solving this easier problem, you must then plug the specific values you have picked into every answer choice, and eliminate any answer choices that do not come out correct. If more than one answer choice has not been eliminated, you can try picking new numbers to eliminate more choices.

Here are some occasions when the strategy of picking numbers will usually work:

• When one or more variables appear in the answer choices.
• When the word “percent” is in the problem (pick 100).
• When there is a variable in the problem, and it is implied that the answer does not depend on the value of the variable.

Here is an Algebra problem where “Picking numbers” can be used.

Which of the following is equal to (x + 66)/22 ?

A. (x+33)/11
B. x+3
C. 3x
D. x/22+3
E. (x+3)/11

Note that you usually want to avoid picking numbers that are too simple. For example, if you choose x = 0, then the answer to the question becomes 3. Now, if you plug a 0 in for x into every answer choice you get the following:

A. 3
B. 3
C. 0
D. 3
E. 3/11

Note that A, B and D are all correct.

See if you can solve this problem by picking a better number. You may also want to try to solve it algebraically.

For examples of applying this strategy see my original blog post on Picking Numbers.

Picking Numbers In Percent Problems

If the word “percent” appears in a problem it’s usually a great idea to choose the number 100. This often works even when there is no variable in the problem.

For examples of picking numbers in percent problems, see my blog post titled Picking Numbers In Percent Problems.

Summary

To summarize, here are some general guidelines for choosing which strategy to use:

• If the answer choices are all numbers, and you are being asked for a simple quantity, try plugging in first.
• If the answer choices are all numbers, and you are being asked for a more complicated quantity, try taking a guess.
• If the answer choices contain variables, try picking a number.
• Any question that mentions percents, pick the number 100.
• In grid in questions with variables, try taking a guess.

There is a lot of information in this blog post with links to many of my other posts, so take your time to read and digest the information. As always, the best way to internalize the concepts above is by practice. For daily practice you may want to check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

Picking Numbers In Percent Problems

Yesterday we looked at the basic but important strategy of picking numbers. Click the following link to view that post: Picking Numbers

At the end of that post, I did say that we would be applying this strategy to percent problems.

When picking a number in percent problems, the best choice is usually the number 100. After all, the word percent literally translates to “out of 100.”

Example 1:

Let’s take a look at an SAT problem involving percents:

There are b bricks that need to be stacked. After k of them have been stacked, then in terms of b and k, what percent of the bricks have not yet been stacked?

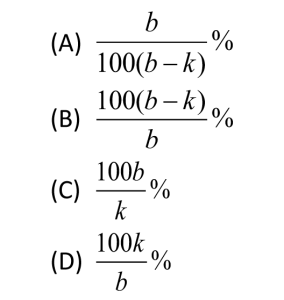
Since this is a percent problem let’s choose 100 for the total number of bricks. So we have b = 100. For k, let’s choose 25, so that 25 bricks have been stacked, and so that means 100 – 25 = 75 have not been stacked. Since we started with 100 as our total, 75% of the bricks have not been stacked. Remember to put a big, dark circle around 75%. We make the substitutions b = 100 and k = 25 into each answer choice.

            (A)   100/7500 ~ 0.0133% (~ means “is approximately”)
            (B)   7500/100 = 75%
            (C)   10,000/25 = 400%
            (D)   2500/100 = 25%

We now compare each of these percents to the percent that we put a nice big, dark circle around. Since A, C and D are incorrect we can eliminate them. Therefore the answer is choice B.

As I always like to stress: B is not the correct answer simply because it is equal to 75%. It is correct because all of the other choices are not 75%. You absolutely must check every choice!

Example 2:

Now let’s look at a percent problem without answer choices. Even though there is no variable in the problem to pick a number for, we can still use the number 100 to solve the problem quickly and easily.

If Matt’s weight increased by 30 percent and Lisa’s weight decreased by 20 percent during a certain year, the ratio of Matt’s weight to Lisa’s weight at the end of the year was how many times the ratio at the beginning of the year?

Again, 100 is the magic number – let’s choose 100 pounds for both Matt’s weight and Lisa’s weight at the beginning of the year. Matt’s weight at the end of the year was then 100 + 30 = 130 pounds and Lisa’s weight at the end of the year was 100 – 20 = 80 pounds. We then have that the ratio of Matt’s weight to Lisa’s weight at the beginning of the year was 100/100 = 1, and the ratio of Matt’s weight to Lisa’s weight at the end of the year was 130/80 = 13/8. We can therefore grid in 13/8.

Side note: 13/8 is equal to 1.625 as a decimal. Thus, we can also grid in 1.62 or 1.63. We get 1.62 by truncating the decimal, and 1.63 by rounding the decimal. Truncating is better because less thought is involved. Note that if you grid in 1.6 the answer will be marked wrong.

So remember the magic number ‘100’ whenever you see a problem with the word “percent” in it… but as always, practice makes perfect – so find more of these problems, such as those found in my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

 

Speak to you soon!

Picking Numbers

The strategy of “picking numbers” works on a wide range of different math problems on standardized tests (such as the SAT, ACT and GRE) in all topics and difficulty levels. It can often be used to make a difficult problem much easier to understand, and if you are careful in its use, you will usually get the answer without too much trouble. The idea is simple – replace the unknowns in the problem with specific values.

Here are some guidelines when picking numbers.

1. Pick a number that is simple but not too simple. In general you might want to avoid picking 0 or 1 (but 2 is usually a good choice).
2. Try to avoid picking numbers that appear in the problem.
3. When picking two or more numbers try to make them all different.
4. Most of the time picking numbers only allows you to eliminate answer choices. So do not just choose the first answer choice that comes out to the correct answer. If multiple answers come out correct you need to pick a new number and start again. But you only have to check the answer choices that have not yet been eliminated.
5. If there are fractions in the question a good choice might be the least common denominator (lcd) or a multiple of the lcd.
6. In percent problems choose the number 100.
7. Do not pick a negative number as a possible answer to a grid-in question. This is a waste of time since you cannot grid a negative number.
8. If your first attempt does not eliminate all choices except one, try to choose a number that is of a different “type.” Here are some examples of types:
   1. A positive integer greater than 1.
   2. A positive fraction (or decimal) between 0 and 1.
   3. A negative integer less than -1.
   4. A negative fraction (or decimal) between -1 and 0.
9. If you are picking pairs of numbers try different combinations from (8). For example you can try two positive integers greater than 1, two negative integers less than -1, or one positive and one negative integer, etc.

Remember that these are just guidelines and there may be rare occasions where you might break these rules. For example sometimes it is so quick and easy to plug in 0 and/or 1 that you might do this even though only some of the answer choices get eliminated.

Examples

Okay, so let’s try solving a math practice problem by picking numbers. The following problem could appear on the ACT or GRE.

Level 4 Number Theory

For nonzero numbers a, b, and c, if c is three times b and b is 1/5 of a, what is the ratio of a² to c² ?

A) 9 to 25
B) 25 to 9
C) 5 to 9
D) 5 to 3
E) 3 to 5

Looks scary? This ACT problem is actually pretty easy if you pick numbers.

Let’s choose a value for a, say a = 5. Then b = 1, c = 3, and therefore the ratio of a² to c² is 25 to 9, choice B.

Simple, right? Maybe a bit too simple? You can of course solve this ACT math problem algebraically as well, but an algebraic solution is more likely to lead to careless errors, and in this problem will actually take more time than picking numbers.

Here is one more math problem for more practice:

Level 4 Algebra

If a = 3^b and b = c + 4 , what is a/27 in terms of c ?

A) c + 1
B) ^c
C) 3^c+1
D) 3^c + 1
E) 3^c + 2

Using the same method as above, let’s pick a number for c, say c = 2. It follows that b = 2 + 4 = 6. So using our calculator, a = 3⁶ = 729. We then have a/27 = 729/27 = 27. Put a nice big, dark circle around this number so that you can find it easily later. We now substitute a 2 for c into each answer choice and use our calculator.

A) 2 + 1 = 3
B) 3² = 9 
C) 3³ = 27
D) 3² + 1 = 9 + 1 = 10
E) 3² + 2 = 9 + 2 = 11

We now compare each of these numbers to the number that we put a nice big, dark circle around. Since (A), (B), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice C.

Remember by picking a number, we can only eliminate answer choices: C is not the correct answer simply because it is equal to 27. It is correct because all four of the other choices are not 27. You absolutely must check all choices!

You can see how powerful picking numbers can be to solve math problems on standardized tests. Follow the guidelines I have provided above and you should be solving more difficult ACT, SAT and GRE math problems with ease. If you would like to see how to apply the strategy of picking numbers to problems involving percents, click the following link: Picking A Number To Solve Percent Problems

More Math Practice Problems

More information on this extremely useful strategy, as well as many more problems to practice with, can be found in the Get 800 collection of test prep books. Click on the picture below for more information about these books.

Until next time…

Taking A Guess – A More Difficult Example

Yesterday I described a very simple yet effective strategy to solve certain math problems on standardized tests such as the ACT and SAT.

The strategy of “taking a guess” is a very useful way to avoid complicated algebra and ensure that a question is answered correctly. See the post from last week for details if you have not already been exposed to this strategy: Basic SAT Math Strategy – Take A Guess

Example

Let’s take a look at another example of how this strategy can be used effectively. Here is a more difficult problem for you to chew the end of your pencil over:

Let the function f be defined for all values of x by f(x) = x(x + 1). If k is a positive number and f(k + 5) = 72, what is the value of k?

Looks tricky?

Well let’s see how we can solve this tricky problem quickly by “taking a guess.”

Let’s take a guess for k, say k = 2. Then we have f(2 + 5) = f(7) = (7)(8) = 56. This is too small. So let’s guess that k = 3 next. Then f(3 + 5) = f(8) = (8)(9) = 72 which is correct. So the answer is 3.

Algebraic Solution

You can see that by using the method of guessing we have found the answer very quickly. Let’s compare this to solving the problem algebraically. Do not worry if the solution that follows confuses you. You will never have to use this method if you choose not to.

f(k + 5) = (k + 5)(k + 6) = k² + 11k + 30.

Since f(k + 5) = 72, we have k² + 11k + 30 = 72. Subtracting 72 from each side of this equation yields

k² + 11k – 42 = 0
(k – 3)(k + 14) = 0

So k = 3 or k = -14. We reject the negative solution because the question says that k is positive. Therefore the answer is 3.

Further Discussion

As you can see, the algebraic solution involves a fairly complicated multiplication which leads to a quadratic equation. The simplest way to solve this quadratic equation is by bringing everything over to one side and factoring. We can see that the answer is obtained correctly, but for most students there is a danger of getting lost in the algebra. This method also takes longer than the method of taking a guess. So for these reasons, why would you want to use algebra to solve a problem such as the example above? Knowing how the algebra works, however, is good for gaining mathematical maturity. This is certainly important if you want to get an 800 in SAT math or a 36 in ACT math. So if you are going for a perfect score, practice the algebraic solution at home. Just do not use it on test day!

More Practice

If you have any questions or comments regarding this strategy, please do let me know. And if you want more practice with this particular strategy, as well as the other important strategies you need to know to improve your standardized test math score, please check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

 

Make sure to join the newsletter above to receive more of my strategies, hints and tips as you prepare for your standardized test!

Taking A Guess

This week I would like to discuss another very basic math strategy for standardized tests such as the ACT and SAT. This strategy is extremely simple to apply and it will often allow you to avoid messy algebraic computations. I call this strategy “Take a Guess.”

Sometimes the answer choices themselves cannot be substituted in for the unknown or unknowns in the problem. But that doesn’t mean you can’t guess your own numbers. Try to make as reasonable a guess as possible, but don’t over think it. Keep trying until you zero in on the correct value.

Example

Let’s see this simple technique in action  with an appropriate math problem.

Bill has cows, pigs and chickens on his farm. The number of chickens he has is three times the number of pigs, and the number of pigs he has is 2 more than the number of cows. Which of the following could be the total number of these animals?

(A)   14
(B)   15
(C)   16
(D)   17
(E)   18

Let’s take a guess and say that Bill has 3 cows. He then has 3 + 2 = 5 pigs, and also 3·5 = 15 chickens. So the total number of animals is 3 + 5 + 15 = 23. This is too big. So let’s guess lower and say that Bill has 1 cow. Then he has 1 + 2 = 3 pigs, and 3·3 = 9 chickens. It follows that the total number of animals is 1 + 3 + 9 = 13, too small. So Bill must have 2 cows, 2 + 2 = 4 pigs, and 3·4 = 12 chickens. Thus, the total we get is 2 + 4 + 12 = 18 animals. So the answer is choice (E).

Note: We were pretty unlucky to have to take 3 guesses before getting the answer, but even so, not too much time was used.

Let’s see what happens when we try to solve this algebraically:

If we let x represent the number of cows, then the number of pigs is x + 2, and the number of chickens is 3(x + 2). Thus, the total number of animals is

x + (x + 2) + 3(x + 2) = x + x + 2 + 3x + 6 = 5x + 8.

So some possible totals are 13, 18, 23, … which we get by substituting in the numbers 1, 2, 3, … for x. Substituting 2 in for x gives 18 which is answer choice (E).

Be warned that many students incorrectly interpret “three times the number of pigs” as 3x + 2. This is incorrect. The number of pigs is x + 2, and so “three times the number of pigs” is 3(x + 2) = 3x + 6. If this confuses you, you can simply avoid this algebra by using the strategy of taking a guess!

You can see that taking a guess is a quick and efficient way to solve this particular SAT math problem. If you begin solving this problem algebraically, then you are much more likely to make a computational error, and ultimately you need to take a guess anyway.

Want More Practice?

More information on this particular strategy, as well as many more problems to practice with, can be found in the Get 800 collection of test prep books.  Click on the picture below for more information about these books.

 

For a more difficult SAT math problem where this strategy is useful, take a look at this post: Taking A Guess – A Further Example Of How To Use This Technique

Plugging In Answer Choices

In many math problems on standardized tests such as the ACT, SAT, and GRE, you can get the answer simply by trying each of the answer choices until you find the one that works. Unless you have some intuition as to what the correct answer might be, then you should always start with choice C as your first guess (on the new SAT you can start with choice B or C because there are four choices instead of five). The reason for this is simple. Answers are usually given in increasing or decreasing order. So very often if choice C fails you can eliminate two of the other choices as well.

There are a few exceptions to this rule. If the word least appears in the problem, then start with the smallest number as your first guess. Similarly, if the word greatest appears in the problem, then start with the largest number as your first guess.

Examples

Let’s take a look at two math problems – one where we start with choice C and one where we do not.

Level 4 Geometry Question

When each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a side of the original square?

A) 3
B) 4
C) 5
D) 6
E) 7

Let’s start with choice (C). If the original length of a side of the square is 5, then the length becomes 8 when we increase it by 3. The original square has an area of 5²= 25 and the new square has area 8² = 64. So the area is increased by 64 – 25 = 39 square inches. Thus, we can eliminate choice (C), and most likely (A) and (B) as well.

We next try choice (D). We have 6² = 36, 9² = 81 and 81 – 36 = 45. Thus, the answer is choice (D).

Here is an algebraic solution for those of you that really want to see it.

Let x be the length, in inches, of a side of the original square. The length of a side of the new square is x + 3. The area of the original square is x², and the area of the new square is:

Thus, the answer is choice (D).

For this particular question, I prefer the solution by starting with choice C to the more tedious and confusing algebraic solution.

Level 3 Number Theory Question

What is the largest positive integer value of k for which 3^k divides 18⁴?

A) 2
B) 4
C) 6
D) 7
E) 8

Note: This type of question is no longer tested on the SAT, but it could show up on the ACT or GRE.

Pull out your calculator. Since the question has the word “largest” in it, we will start with the largest answer choice which is choice (E), and we will divide 18⁴ by 3⁸. We type 18^4 / 3^8 into our calculator and the output is 16. Since 16 is an integer, the answer is choice (E).

Note that all five answer choices give an integer, but 8 is the largest positive integer that works.

Here is a direct solution for those of you who really want to see it.

The prime factorization of 18 is 18 = 2·3². Therefore:

18⁴ = (2·3²)⁴ = 2⁴(3²)⁴ = 2⁴3⁸.

From this prime factorization it should be clear that 3⁸ divides 18⁴, but 3⁹ does not.

Again, for this particular question, most students will prefer the easier solution of starting with choice E (the largest answer choice) to the more confusing algebraic solution.

More Math Practice Problems

More information on this extremely useful strategy, as well as many more problems to practice with, can be found in the Get 800 collection of test prep books. Click on the picture below for more information about these books.

Plugging In – Part 1

 

Plugging In – Part 2

Speak to you soon!

Even and Odd Functions

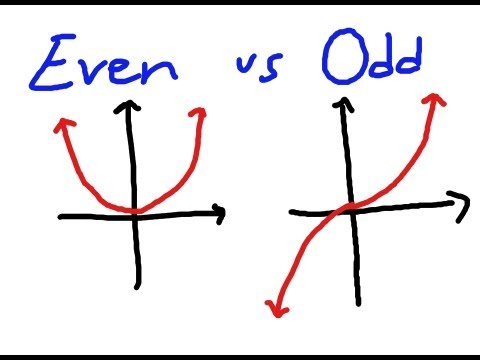
A function f with the property that f(–x) = f(x) for all x is called an even function.

Example 1: f(x) = |x| is an even function because

f(–x) = |–x| = |x| = f(x).

A function f with the property that f(–x) = –f(x) for all x is called an odd function.

Example 2: g(x) = 1/x is odd because

g(–x) = 1/(–x) = –1/x = –g(x).

A polynomial function is a function for which each term has the form axⁿ where a is a real number and n is a positive integer.

Polynomial functions with only even powers of x are even functions. Keep in mind that a constant c is the same as cx⁰ , and so c is an even power of x.

Example 3: Here are some examples of polynomial functions that are even.

f(x) = x²

g(x) = 4

h(x) = 3x⁸ – 2x⁶+ 9

Polynomial functions with only odd powers of x are odd functions. Keep in mind that x is the same as x¹, and so x is an odd power of x.

Example 4: Here are some examples of polynomial functions that are odd.

f(x) = x³

g(x) = x

h(x) = 3x¹¹ – 2x⁵+ 9x

A quick graphical analysis of even and odd functions 

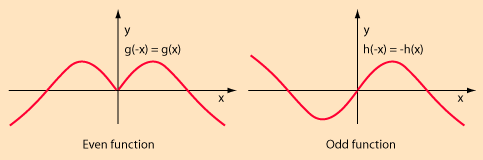
The graph of an even function is symmetrical with respect to the y-axis. This means that the y-axis acts like a “mirror,” and the graph “reflects” across this mirror.

The graph of an odd function is symmetrical with respect to the origin. This means that if you rotate the graph 180 degrees (or equivalently, turn it upside down) it will look the same as it did right side up.

So another way to determine if f(–x) = f(x) is to graph f in your graphing calculator, and see if the y-axis acts like a mirror (see the function g in the figure above).

Another way to determine if f(–x) = –f(x) is to graph f in your graphing calculator, and see if it looks the same upside down (see the function h in the figure above).

These two techniques will work for all functions (not just polynomials).

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

If you have any questions on this topic, then please post them in the comments below.

Speak to you soon!

by Dr. Steve Warner

Hello everyone and welcome to my first educational book review. In my ongoing quest to help as many students as possible realize their full scholastic potential I am always looking for new teaching and learning methods. One of the biggest questions I am constantly thinking about is “why is it that some students seem to have very little trouble absorbing and retaining information, while for other students these tasks seem almost impossible?” More importantly, are there certain methods that a “smart” student is using that a struggling student can replicate to become “smarter?” Well author Scott Young seems to think so and he claims to teach these methods in his book “Learn more, study less.”

Click here to visit the website

As an educator I felt compelled to read through this book carefully with an open mind. Before I discuss some of the details about the book, I think that it is important that you understand how I would classify myself as a learner.

A bit about me

Throughout elementary school, high school, and college I never had any trouble learning. I would absorb and retain the information taught to me very quickly. I spent very little time outside of the classroom studying. I was always very “book smart.” Well at least until graduate school. When I began my graduate program in mathematics I struggled to understand the material for the very first time. There were huge gaps in my  knowledge that needed to be filled, and my level of mathematical maturity was not high enough to be able to solve homework problems. But I worked extremely hard, and by my second year of graduate school I was no longer struggling and other students were coming to me for help.

If you asked me a week ago why I was always so smart in school, I would not have been able to give you a reasonable answer. If you asked me how I went from struggling in my first year of graduate school to becoming top of my class in the second year I would have given an incomplete answer at best. But now, after reading Scott Young’s book I believe that I can give a pretty clear explanation. During my time in school I have used almost every technique that Scott describes. At the time I never would have thought to describe what I was doing as “using techniques,” but I suspect that if I were to describe these methods to a “slow learner,” they would not be familiar with them, and might find them helpful.

Click here to visit the website

What is in the book?

In “Learn more, study less,” Scott Young describes what he calls “holistic learning.” Holistic learning is essentially the opposite of rote memorization. The methods that he describes are very simple to understand. Some can be applied very quickly and others may require a concentrated effort on the part of the student.

An example of a simple technique described in the book is the link method. This is a good method to use when you are forced to memorize a sequence of arbitrary information. This method involves creating vivid and exaggerated mental images that associate two symbols in the sequence. For example, we could link the entry “tiger” with the entry “tennis ball” by creating an image of a tiger standing upright juggling three tennis balls. This image is so ridiculous that it would be almost impossible to forget.

An example of a more advanced technique is what Scott calls visceralization. This is similar to visualization, but allows for the possibility of involving sounds, sensations, and emotions in addition to simply imagining a mental picture.

Click here to visit the website

My thoughts on “Learn more, study less”

There is nothing that I have read in this book that I would consider “groundbreaking.” As I have said, once I read the book I realized that I have been using these techniques my whole life. I just never put a label on any of them. But I am really happy that I read it. I now have a way to describe, in simple terms, methods of studying that I believe can be effective for many students. When a student comes to me with retention issues, I now have a list of suggestions I can recommend to help them.

I think this is definitely a great book for educators to read. Academics that read this book will probably realize they have been using at least some of the techniques presented here their whole lives. After reading the book they will be able to describe these methods more easily to their students that are having retention issues.

Will the information in this book help students? Well I cannot answer this with 100% certainty since I have not tested it, but I am fairly confident that these techniques will work for some, if not many, students. If you are a student struggling to absorb and retain information, then I think that investing in this book would be a good decision. Try one or two of the techniques out for a month or two. I suspect that your scholastic performance will improve. If not, it was just a small time investment, and you can get your money back for the book (Scott Young has a four month return policy).

Click here to visit the website

Final Analysis

“Learn more, study less” is a really interesting book. Reading it has allowed me to name and describe some of the learning methods I have been using my whole life. I think that it is an especially good resource for educators. And for the struggling student I say “give it a try.” My gut feeling is that it will be extremely helpful for some students, and at the very least somewhat helpful for most students. Get the book, practice one or two of the methods that you connect with for a couple of months. My guess is that it will be a positive experience.

Final Score: 9/10

Click here to visit the website

Note:  There is actually a full video course available as well. At this point in time I have only read the book, so I cannot give any feedback regarding the course.

Extra Bonus

If you visit the “Learn more, study less” website using a link on this page, and then purchase either the book or video course, I will give you a free PDF of the “SAT Prep Math Survival Guide.” Simply forward your order confirmation email to steve@SATPrepGet800.com to receive your free bonus.

Click here to visit the website

Full Disclaimer: I have received no compensation for this review. Scott Young did provide me with all materials at no charge, but I have no personal interest in this product.

I spent several days reading this book carefully, and the opinions that I have shared about this book are all my own. I take great pride in providing accurate, useful, and honest information to my audience.

The links in this blog post are affiliate links. If you click on one of these links and decide to make a purchase I will receive a commission on the sale. This does not cost you anything additional. These small commissions help to keep the rest of the content on my blog free, so thank you!

Free Proctored Exam

Sullivan Tutorials, in cooperation with Get 800, are inviting you to Staten Island, NY to take a free proctored PSAT. The test will be available on

May 12th from 6:30 – 9:30 P.M    OR    May 15th from 1:00 P.M. – 4:00 P.M.

We will be testing students to see if they can make it into one our National Merit prep groups. There is no charge to take this proctored test and there is no obligation to sign up for a course. To save yourself a seat, please send an email to:

steve@SATPrepGet800.com

You will receive the testing location via email.

About Sullivan Tutorials

For the past 25 years, Sullivan Tutorials has been responsible for about 60% of all the National Merit Semi-Finalists and all but a few of the Finalists on Staten Island. Students are placed in groups of 5-6 students with similar math scores. Groups meet for math sessions in the home of one student and for verbal sessions in the home of another student in the group.

National Merit Students

Students that make it into one of the National Merit groups will start meeting on weekday evenings in mid-July. They will meet for two 3 hour verbal sessions and two 2 hour math sessions in July and August and then 2 hour sessions once a week right up to the PSAT in October. They will then take the PSAT in October, and the SAT in Nov, Dec and Jan.

This is a very difficult year as the SAT has changed radically. To see some of the major changes, take a look at this article I wrote a while back: Preview the Math Changes on the “New” SAT

In addition, here are some of the changes in SAT Verbal:

• The essay will be optional – individual institutions will decide if they require the essay.
• There will be a 65 minute reading section.
• There will be a 35 minute language and writing section.
• There will no longer be sentence completions.
• There will be a greater emphasis on the meaning of words in extended contexts, and on how word choice shapes meaning, tone and impact.

Other Students

Students who do not make into one of the National Merit groups may start preparing with Sullivan Tutorials in mid-August to take the November, December and January exams if they are fairly strong in math and have scores that are reasonably high. All other students will begin preparing in January and take the new May exam.

Meetings in May will start with a 15 minute Q & A for parents and then students will take a 2 hour and ten minute PSAT. These exams will be graded before the students leave. Parents can either have a consultation right then, or they can do so by phone during the week after the exam.

National Merit Information

There are three levels for the National Merit. The first is 201 pts and up which is Commended Student. This information goes to any two colleges that the student designates. The second and more important level is Semi-Finalist. The cut off for this varies between 215 and 219 in New York State. 218 is the most common number. Students who get this are considered elite – most colleges want these students for bragging rights. These students are informed in early September of their senior year that they are semi-finalists and they are given the opportunity to write an essay that is evaluated by a committee. The top 1000 students in America are then designated as Finalists. Scholarship money is attached to this designation. On the aegis of becoming a finalist, many students are eligible for full scholarships to some of their chosen schools.

Once again, to save yourself a seat for the proctored exam, please send an email to:

steve@SATPrepGet800.com

Two Deadly Algebra Mistakes That You Need To Fix Right Now

Today I would like to go over two very common mistakes that students make when solving algebra problems that lead them to the wrong answer. These two errors are very basic and easily fixed. But surprisingly, even students in college calculus classes are still making these mistakes. Many students will make one of these mistakes on their SAT, ACT, or GRE, thus lowering their score. The good news is that if you just take a few minutes to read this article carefully, you will probably never make these two mistakes again. So please, don’t be another statistic. Read and absorb the information in this article right away. And if you want to discuss other common algebraic mistakes, please bring them up in the comments below.

Algebra Mistake Number 1

Let me start with a very simple math problem. What is –3² equal to?

Please take your time to answer this question yourself before looking at the answer.

Is the answer 9 or –9?

The answer is in fact –9.

Most of the time when I tell students the answer they say “but I thought when you square a negative number it becomes positive.”

And in fact, they are right. When you square a negative number it does become positive. But that is not what is going on here.

Don’t worry if you got this wrong. It does not mean you are not intelligent. It has nothing to do with your problem solving skills. It has only to do with a very small gap in knowledge which we will correct right now.

There are actually two issues that need to be addressed here.

Point 1: The first thing that you need to understand is that the expression –x is equivalent to the expression (–1)x. In other words, the operation of negation is equivalent to multiplication by –1.

Point 2: The second thing that you need to understand is the basic order of operations. In particular, exponentiation is always done before multiplication.

Note that the order of operations that we as humans currently use is a completely man-made construction. There is no really good reason that we do one operation before another one, except that a long time ago someone decided that this is the way we are going to do things.

So now, let’s get back to our computation.

By Point 1 above we have –3² = (–1)3². By Point 2, we must perform the exponentiation first. So we have –3² = (–1)3² =(–1)9 = –9.

Note: Although –3² = –9, we do have that (–3)² = 9. The reason is that in the latter case we are squaring a negative real number, and squaring a negative real number does always give a positive number.

Let’s try another example involving functions:

If f(x) = –x² + 5, then what is f(2)?

Solution: f(2) = –2² + 5 = –4 + 5 = 1.

Did you get that one correct? If not, reread this section until you can explain your error.

Try this similar question:

If f(x) = –x² + 5, then what is f(–2)?

Solution: f(–2) = –(–2)² + 5 = –4 + 5 = 1.

Note that the solution to this question is pretty much identical to the last one. This is because (–2)² is the same as 2². See the note above if you are still having trouble with this.

Algebra Mistake Number 2

Let’s look at another pretty basic math problem. Can you expand the expression –(x + 2)?

Again, please take your time to answer this question yourself before looking at the answer.

Did you get –x + 2, or –x – 2 ?

The answer is in fact –x – 2.

When negating an expression with two terms, many students forget to distribute the minus sign correctly.  In this case, both terms need to be negated.

If it helps you, you can rewrite –(x + 2) as (–1)(x + 2). Then we get

(–1)x + (–1)2 = –x – 2.

If you are okay with distributing in general, but only have trouble with this specific instance, then this might help. If this doesn’t help, then you need to go over the distributive property very carefully.

As another example, try to simplify this expression:

(x – 3) – (x – 5)

Let’s begin by removing the parentheses and distributing the subtraction symbol in the middle correctly:

x – 3 – x + 5

Finally we combine like terms to get an answer of 2.

Avoid Making Other Common Mistakes On Standardized Tests

If you want to learn how to avoid all the traps that occur in the math sections on standardized tests such as the SAT, ACT, and GRE, as well as learn all the most important math strategies, then take a look at the Get 800 collection of test prep books.  Click on the picture below for more information about these books.

If you have any questions on this topic, then please post them in the comments below.

Speak to you soon!