500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Abstract Algebra for Beginners
Coming Soon

Today I would like to announce that I will be releasing my new book Abstract Algebra  for Beginners shortly. This book was written to provide a rigorous but easy to follow introduction to the subject of Abstract Algebra.

The book will be released within the next two months at a special promotional price.

To be added to the notification list, simply send an email to steve@SATPrepGet800.com with “Notify me” written in the subject line.

If you think your friends might be interested in being notified of this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Why Do We Use the Real Numbers?

Let’s quickly recall a few basic sets of numbers:

In particular, the set of rational numbers consists of all fractions, where the numerator (number on top) and denominator (number on bottom) are integers (and the denominator is not 0). Here are some examples of rational numbers:

If the denominator is 1, we will identify the rational number with the integer consisting of the numerator alone. If the numerator is 0, we will identify the rational number with the integer 0. For example, we have:

At first glance, it would appear that the  rational numbers would be sufficient to solve all “real world” problems. So, why do we use the real number system? The real number system is so complicated to understand that teachers in elementary school, middle school, and even in high school do not even attempt to define it rigorously.

Well, it turns out that a long time ago, a group of people called the Pythagoreans showed that the rational numbers alone are actually not enough to solve all real world problems. The issue was first discovered when applying the now well-known Pythagorean Theorem.

The Pythagorean Theorem: In a right triangle with legs of lengths a and b, and a hypotenuse of length c, c² = a² + b².

Proving the Pythagorean Theorem is not too difficult and in fact, I have given an elementary proof here: Proving the Pythagorean Theorem

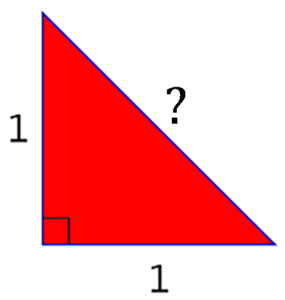
So, how does the Pythagorean Theorem tell us that the rational numbers are not enough? The answer lies in the following simple picture:

Question: In a right triangle where both legs have length 1, what is the length of the hypotenuse?

Let’s try to answer this question. If we let c be the length of the hypotenuse of the triangle, then by the Pythagorean Theorem, we have c²  = 1²  + 1²  = 1 + 1 = 2. Since c²  = c ⋅ c, we need to find a number with the property that when you multiply that number by itself you get 2. The Pythagoreans showed that if we use only rational numbers, then no such number exists.

Theorem: There does not exist a rational number a such that a²  = 2.

The proof of this theorem, although not too difficult, does require a bit of mathematical knowledge. Over the next few weeks, I will be teaching you the mathematics necessary to prove this theorem, with the ultimate goal of supplying a proof.

As it turns out, there is a real number a such that a²  = 2 (in fact, there are two such real numbers). In order to prove this, we would first need to give a rigorous definition of the real numbers. This requires a lot more work than one would initially expect.

The details of this definition are developed in my math books Pure Mathematics for Beginners, Set Theory for Beginners, and Topology for Beginners. These books contain no prerequisites and are perfect for anyone just starting out in theoretical math. You can get them all for one low price by clicking on the image below.

 

Coauthors Wanted for New Math Books

Due to the success of my Pure Math for Beginners book series, I am planning on extending this series to include more basic books like Algebra, Trigonometry, Precalculus, Calculus, etc. I’m currently accepting applications for potential coauthors that would be interested in helping me write these books. I’m offering a 10% royalty to those working with me for the first time with the opportunity for higher royalties for future books. If you are interested, please fill out an application and submit your resume here:

Get 800 Job Application

If you have any questions please feel free to contact Dr. Steve Warner directly at

steve@SATPrepGet800.com

Special Offer – Pure Math Paperback Bundle

Many of our customers have been asking if it is possible to purchase several of our pure math books for beginners in paperback for a discounted price. To meet this demand, we are pleased to introduce a special promotional package that includes all three of our pure math beginner books for the price of just $99. Shipping and all other fees are included in this price. By purchasing all three of Dr. Steve Warner’s pure math books as a bundle, you will save more than 25%, as compared to buying the books individually. The books included in this special promotion are:

• Pure Mathematics for Beginners
• Set Theory for Beginners
• Topology for Beginners

Note that if you were to buy each of these books separately the total price would be $133.97, plus taxes and possibly shipping. By purchasing the books here you will get all three books in paperback for just $99. This is more than a 25% savings.

Due to the bulk discount on this special offer, all sales are final (no refunds).
Please allow up to 14 days for processing and shipping.

To place your order simply click the following button.

For more information about these books you can visit each book’s Amazon page by clicking each book image below:

If you have any questions or concerns please feel free to contact Dr. Steve Warner directly at

steve@SATPrepGet800.com

Thank you all for your continued support!

The 29 Topologies on a 3 Element Set

A topological space consists of a set (a collection of objects) S together with a collection T  of subsets of S, which we call “open sets.” This collection of subsets has to satisfy the following properties:

• ∅ (the empty set) and the set S itself must be in T.
• The union of any members in T  must be in T.
• The intersection of finitely many members in T  must be in T.

In this post, I will discuss the topologies on the set consisting of the three distinct elements a, b, and c:

S = {a, b, c}

Although topologies on finite sets aren’t particularly useful in practice, they are a great tool for learning what a topology is and eliminating any misconceptions that one might have.

There are 29 topologies on the three element set S. Let’s look at a few of them.

We have the trivial topology:

T₁ = {∅, {a, b, c}}.

If we throw in just a singleton set (a set consisting of just one element), we get the following three topologies:

 T₂ = {∅, {a}, {a, b, c}}
T₃ = {∅, {b}, {a, b, c}}
T₄ = {∅, {c}, {a, b, c}}

Note that we can’t throw in just two singleton sets. For example, the following collection is not a topology on S:

{∅, {a}, {b}, {a, b, c}}

Do you see the problem? It’s not closed under taking unions:

{a}  and {b} are there, but {a, b} = {a} ∪ {b}  is not!

However, the following  is a topology on S:

T₅= {∅, {a}, {b}, {a, b}, {a, b, c}}

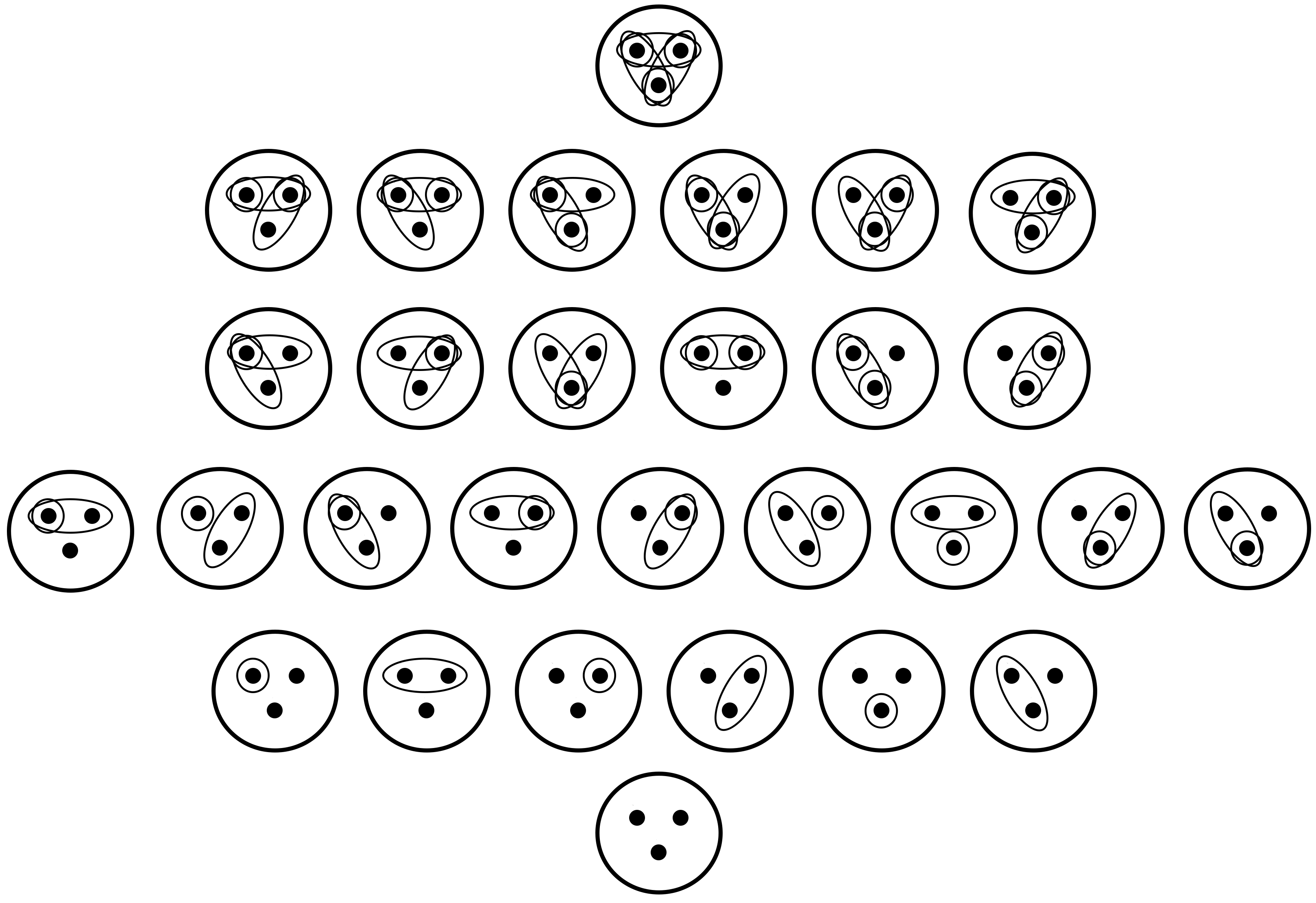
Below is a picture of all 29 topologies on {a, b, c}  (to avoid clutter we left out the names of the elements). A large circle surrounds a, b, and c in all cases because S = {a, b, c}  is in all 29 topologies. Also, it is understood that the empty set is in all these topologies.

I organized these topologies by the number of sets in each topology. The lowest row consists of just the trivial topology. The next row up consists of the topologies with just one additional set (three sets in total because ∅ and S are in every topology), and so on.

The topology {∅, {a}, {a, b, c}} is finer than the topology {∅, {a, b, c}} because {∅, {a, b, c}} ⊆ {∅, {a}, {a, b, c}}. We can also say that {∅, {a, b, c}} is coarser than {∅, {a}, {a, b, c}}. The topologies {∅, {a}, {a, b, c}}  and {∅, {b}, {a, b, c}} are incomparable. Neither one is finer than the other. To help understand the terminology “finer” and “coarser,” we can picture the open sets as a pile of rocks. If we were to smash that pile of rocks (the open sets) with a hammer, the rocks will break into smaller pieces (creating more open sets), and the pile of rocks (the topology) will have been made “finer.”

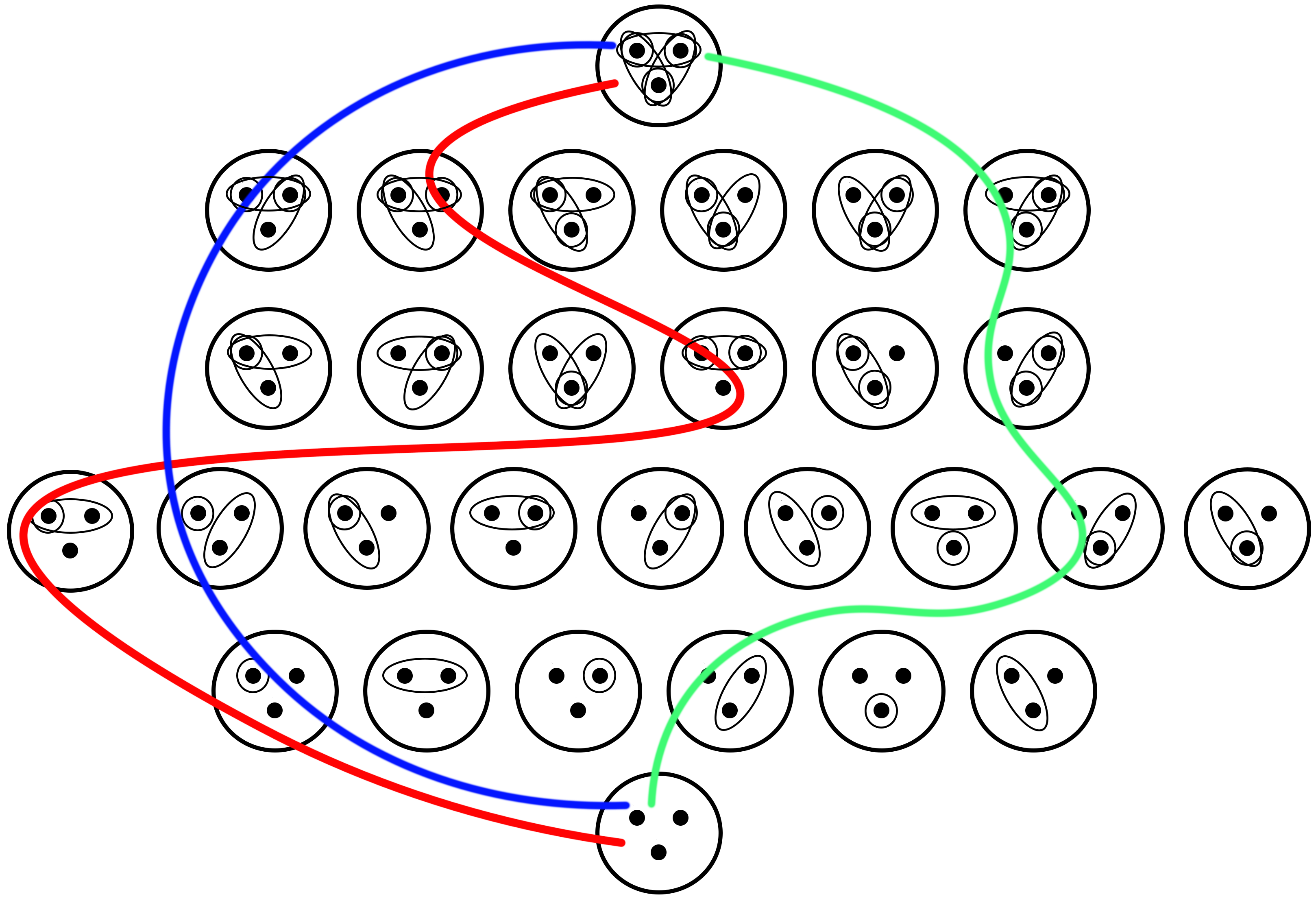
Below we see a visual representation of three “chains” of topologies. As each path moves from the bottom to the top of the picture, we move from coarser to finer topologies.

Although there are 29 distinct topologies on a 3-element set, many of them are topologically equivalent. Informally, two topological spaces are topologically equivalent if there is a one-to-one correspondence between the elements of the two spaces that also provides a correspondence between their open sets. Below is a picture of just 9 of the topologies we have seen. Each of the 29 topologies pictured above is topologically equivalent to one of these 9, and none of these 9 are topologically equivalent to each other.

If you want to begin learning some more advanced mathematics, you may want to check out either Pure Mathematics for Beginners or Topology for Beginners. These books contain no prerequisites and are perfect for anyone just starting out in theoretical math.

Topology for Beginners
Just 14.99 on Amazon

Hi everyone! Topology for Beginners is now available in paperback from Amazon. This book, consisting of 16 lessons, provides a rigorous introduction to basic and intermediate topology. Explanations to all the problems in the book are included as a downloadable PDF file.

The paperback is now on sale on Amazon for only $14.99. Note that once the sale ends (in about 24 hours), the price of this book will go up to $39.99.

The promotion is over. Thanks to all who participated. The book is available at Amazon here: Topology for Beginners

If you have any questions, feel free to contact me at the following email:

steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Proving the Pythagorean Theorem

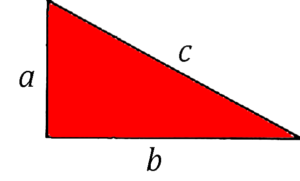
There are many ways to prove the Pythagorean Theorem. Today I would like to share one of my favorite methods. I like this method because it’s simple, elegant, and easy to follow. Let’s begin with a few basic definitions, followed by a statement of the theorem:

The picture above shows a right triangle. The vertical and horizontal segments (labeled a and b, respectively) are called the legs of the right triangle, and the side opposite the right angle (labeled c) is called the hypotenuse of the right triangle

The Pythagorean Theorem: In a right triangle with legs of lengths a and b, and a hypotenuse of length c, c² = a² + b².

Notes: There are many ways to prove the Pythagorean Theorem. Here, we will provide a simple geometric argument. For the proof we will want to recall the following:

• The area of a square with side length s is A = s².
• The area of a triangle with base b and height h is A = 1/2 bh.

Notice that in our right triangle drawn above, the base is labeled b, and the height is labeled a. So, the area of that right triangle is

A = 1/2 ba = 1/2 ab.

Now, let’s prove the theorem!

Proof of the Pythagorean Theorem: We draw 2 squares, each of side length a +b, by rearranging 4 copies of the given triangle in 2 different ways:

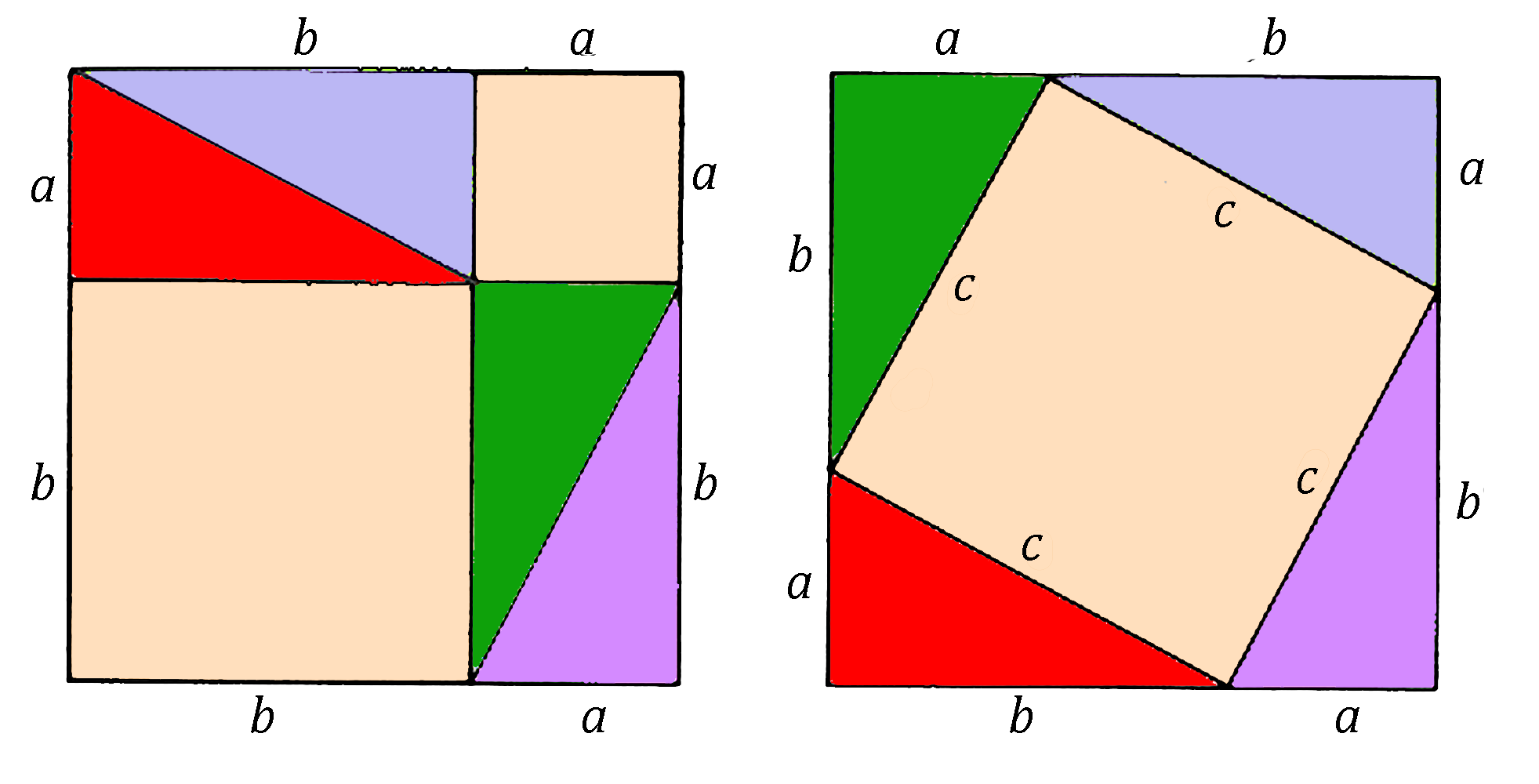
We can get the area of each of these squares by adding the areas of all the figures that comprise each square.

The square on the left consists of 4 copies of the given right triangle, a square of side length a and a square of side length b. It follows that the area of this square is

4 ⋅ 1/2 ab + a² + b² = 2ab + a² + b².

The square on the right consists of 4 copies of the given right triangle, and a square of side length c. It follows that the area of this square is

4 ⋅ 1/2 ab + c² = 2ab + c².

Since the areas of both squares of side length a + b are equal (both areas are equal to (a + b)² ), we have

2ab + a² + b² = 2ab + c².

Cancelling 2ab from each side of this equation yields

 a² + b² = c².

And there you have it…a relatively simple proof of the Pythagorean Theorem.

If you enjoy thinking about why things like this are true or you want to begin learning some more advanced mathematics, you may want to check out either Pure Mathematics for Beginners or Set Theory for Beginners. These books contain no prerequisites and are perfect for anyone just starting out in theoretical math.

Why Can’t We Divide By Zero?

Whenever I ask a student why we can’t divide by zero I always get strange answers. Most students just restate the question in another way. Some typical answers are “because division by 0 is impossible,” “because my teacher told me I can’t,” or “because my calculator gives an error when I try to do it.”

But none of these “answers” explain anything.

We will clear up this mystery by the end of this post.

Some of the questions we will answer in this post are the following:

1. What does it mean for an integer to be divisible by another integer?
2. Is zero divisible by every integer?
3. Are there any integers that are divisible by zero?

This is a pretty technical article with some fairly sophisticated mathematics.

We say that 42 is divisible by 7 because 42 = 7 · 6. The number “6” itself isn’t particularly important here, but what is important is that 6 is an integer. In other words, 42 is divisible by 7 because there is an integer k such that 42 = 7k.

In general, an integer n is divisible by an integer d if there is another integer k such that n = dk.

In practice we can check if n is divisible by d simply by dividing n by d in our calculator (or sometimes by using the divisibility tricks I mention in this video: Divisibility Tricks). If the answer is an integer, then n is divisible by d. If the answer is not an integer (it contains digits after the decimal point), then n is not divisible by d.

For example, when we divide 42 by 7 we get 6, an integer. So 42 is divisible by 7.

As another example, every integer n is divisible by 1. This is true because n = 1 · n, and n is an integer.

What about the integer 0? Is 0 divisible by 7?

Yes it is because 0 = 7 · 0, and 0 is an integer.

In fact, if m is any nonzero integer, then 0 is divisible by m. This is true because 0 = m · 0.

This fact is worth emphasizing since students often get confused by it.

Zero is divisible by every nonzero integer!

Note in the bold statement above the word “nonzero.” Isn’t 0 also divisible by 0 according to that definition? After all, if we set m = 0 in the equation “0 = m · 0,” we then get 0 = 0 · 0 which is a true statement! We will talk about this more in just a bit.

Let’s now check if there are any integers n which are divisible by 0. If n is divisible by 0, then there is an integer k such that n = 0 · k. However, we have 0 · k = 0. So, if n is divisible by 0, it follows that n must be equal to 0.

In other words, there are no nonzero integers that are divisible by 0!

Note that we have not shown that 0 is divisible by 0. We only proved the conditional statement “if an integer is divisible by 0, then that integer must be 0.” We still need to check if 0 actually is divisible by 0.

So let’s assume for a moment that 0 is divisible by 0. This means that there is an integer k such that 0 = 0 · k. But every single integer satisfies this equation. Just to pick two specific values, 0 and 1 both satisfy this equation. This means that 0/0 = 0 and 0/0 = 1. It follows that 0 = 1. But 0 and 1 are different integers. It follows that 0 cannot be divisible by 0.

Thinking more deeply like we have done here can help raise your level of mathematical maturity. The question of why division by zero is not possible is one of the big holes students have in their understanding, so I hope that after reading this post you are now a little wiser!

If you enjoy thinking about why things are true or you want to begin learning some more advanced mathematics, you may want to check out either Pure Mathematics for Beginners or Set Theory for Beginners. These books are perfect for anyone just starting out in theoretical math.

Topology for Beginners
Coming Soon

Today I would like to announce that I will be releasing my new book Topology for Beginners shortly. This book was written to provide a rigorous but easy to follow introduction to the subject of Topology.

The book will be released within the next two months at a special promotional price.

To be added to the notification list, simply send an email to steve@SATPrepGet800.com with “Notify me” written in the subject line.

If you think your friends might be interested in being notified of this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Gaining Mathematical Maturity

Today I would like to talk about mathematical maturity and how it relates to your performance on standardized tests such as the SAT, ACT, and GRE. Although there is no single agreed upon definition of mathematical maturity, I would define it as “one’s ability to analyze, understand, and communicate mathematics.”

There is no strict measure of mathematical maturity, but let’s examine what various levels of mathematical maturity might look like:

• Level 1: These students can do basic high school math when taught in a classroom setting. Students at level 1 can solve basic algebra and geometry problems by following the procedures that were taught to them. If such a student were asked, “Why does this work?” they will not be able to verbalize a satisfactory answer. Most high school students are at this level.

• Level 2: These students can learn basic mathematics without any outside help. Students at level 2 can read an algebra or precalculus book on their own  and can probably explain basic mathematics to other students. If shown how to do a problem, they will be able to solve problems that are similar using the same strategy. These students would have no problem in a Calculus course.

• Level 3: These students can learn advanced mathematics on their own. Students at level 3  can not only do problems, but can also explain why the methods they are using work. They can often solve problems in several different ways and develop their own techniques for solving problems. These students will be able to solve problems of a type that they have never seen before as long as they know the appropriate definitions and relevant background material.

These “levels” are just here to illustrate a point. It is often hard to pinpoint the exact level of a student. Some students naturally have a higher level of mathematical maturity than others. For example, students taking AP Calculus usually have a higher level of mathematical maturity than a student in remedial algebra. As such, the AP Calc student is more likely to do better in math on the standardized tests.

Simply knowing more mathematics is not enough to guarantee a higher level of mathematical maturity. An AP Calculus student does not have a higher level of mathematical maturity simply because they know more math. It is because they have been attempting problems that require a higher level of thinking.

The good news is that mathematical maturity can be increased. Doing so will greatly improve your problem solving ability as well as increase your math score on the SAT. Here are a few ways you can increase your level of mathematical maturity.

• Do SAT/ACT/GRE math problems. If you can currently only solve Level 1 geometry problems, and a month from now you can solve Level 2 geometry problems, then guess what—you have increased your level of mathematical maturity. So keep doing SAT (or ACT, etc.) problems a level above your current ability until the day of the test. If you have only about 3 months before your test, then this is the method you should employ most.

• Learn some mathematics by yourself. This may seem contrary to what has already been stated—but it is not. Knowing more mathematics will probably not raise your score very much, especially if the math is hand fed to you. But the process of learning mathematics will increase your mathematical maturity. What kind of math should you learn? It does not matter! Pick something you find the most enjoyable, and try to learn it on your own. If you get stuck, then ask for help—but developing the skill to learn math yourself will definitely increase your mathematical maturity. This strategy is more long term and you should consider it if you have 6 months or more before your standardized test. If the idea of learning advanced math on your own seems scary to you, you may want to check out either Pure Mathematics for Beginners or Set Theory for Beginners. These books are perfect for anyone just starting out in theoretical math.

• Attempt difficult math problems. There are a lot of challenging math problems out there that only require the math that you already know. There are math magazines (yes, I know these sound like a lot of fun!), websites, and books full of problems. Pick a few and struggle with them. Just trying difficult problems and developing strategies will increase your mathematical maturity, even if you never solve a single one on your own. Also, solving problems using the advanced methods that are described in the many books I have written will boost your level of mathematical maturity.

I can still remember the day I got back my first real analysis homework as a first year graduate student at Rutgers University. I received a 62. This is by far the lowest grade I had ever received in mathematics. The worst part was that I had spent many hours on this homework, and I thought that it was completely correct. I remember approaching my teacher explaining that I never received such a low math grade, begging for him to tell me what to do. But he did not have an answer for me. I was on my own.

That whole first year of graduate school was a struggle. I wound up with B’s in most of my classes despite working harder than I had ever worked in my life. I was  unprepared for how difficult graduate school was, especially after receiving a 4.0 Math GPA as an undergraduate with very little effort.

This was quite disheartening and I thought that there was no way I would be able to do mathematical research and get my Ph.D. I just was not smart enough.

But an interesting thing happened during my second year. Apparently my hard work paid off. All of a sudden nothing seemed difficult anymore — I was back at the top of my class. Despite the fact that I was taking even harder classes than the previous year I was breezing through them with very little effort.

All of a sudden I was able to read advanced graduate texts on my own and do the problems at the end of each section without any help from others. What happened? Did I all of a sudden accumulate a massive amount of mathematical knowledge. The answer is no. In fact, this would not have helped. The mathematical language in my new classes was actually quite different from what I had learned the previous year.

What happened is that by struggling so hard the year before with little to no help from others, I managed to increase my level of mathematical maturity. Things that I did not stand a chance of understanding just a year earlier now made perfect sense. Other students were now coming to me for help, and I was able to help every single one of them. To think just a year earlier I was considering dropping out because it was just too hard. What a shame that would have been.

My level of mathematical maturity had to take several more jumps before I would graduate. Mathematical research is highly sophisticated and requires a clever mind that is willing to think in unconventional ways. The one thing that my years at graduate school have taught me is that anyone is capable of doing anything that they set their mind to.

Just don’t give up and you will persevere!

P.S. If you are preparing for a standardized test, you might want to take a look at the Get 800 collection of test prep books.