500 New SAT Math Problems
Just 19.99 on Amazon
Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.
The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.
The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems
If you have any questions, feel free to contact me at steve@SATPrepGet800.com
Thank you all for your continued support!
A Trick For Free Two Day Shipping
I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.
Sign Up For Amazon Prime For Free
If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.
This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.
After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.
Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.
Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:
Sign Up For Amazon Prime For Free
If you think your friends might be interested in this special offer, please share it with them on Facebook:
Thank you all for your continued support!
 |
 |
 |
 |
 |
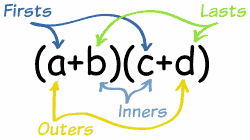To FOIL or Not to FOIL
Most students are familiar with the mnemonic FOIL to help them multiply two binomials (polynomials with 2 terms) together. As a simple example, we have
(x + 1)(x – 2) = x2 – 2x + x – 2 = x2 – x – 2
I do not particularly like teaching this method for multiplying binomials for the following reasons:
- This method works ONLY for binomials. It does not extend to polynomials with more than 2 terms.
- It requires learning something new. There is already an algorithm that works very well that simulates a method students already know.
- Most students after learning HOW to FOIL will not be able to explain WHY it works.
- From a theoretical point of view it is inefficient. FIOL is actually the better choice.
Some of you might be saying “But FOIL is so simple and easy to remember. What can possibly be better?” The answer is an algorithm that everyone already knows.
This post is especially relevant for students taking the ACT.
Quick Review of Multiplication
As a quick review, let’s multiply two 2-digit numbers together, say 12 and 32:
12
32
We begin by multiplying the 2 on the bottom by each digit on top, moving from right to left:
12
32
24
We then multiply the 3 on the bottom by each digit on top, moving from right to left. This time as we write the answers we leave one blank space on the right:
12
32
24
36
Finally, we add:
12
32
24
36
384
Voila!
A Better Algorithm For Multiplying Polynomials
We are now going to use essentially the same algorithm for multiplying our first two binomials above together. Notice that for multiplying numbers I chose an example where no carrying was necessary. When multiplying polynomials you will NEVER have to carry.
x + 1
x – 2
We begin by multiplying the -2 on the bottom by each term on top, moving from right to left. First note that -2 times 1 is -2:
x + 1
x – 2
–2
Next note that -2 times x is -2x:
x + 1
x – 2
–2x – 2
Now we multiply the x on the bottom by each term on top, moving from right to left. This time as we write the answers we leave one blank space on the right:
x + 1
x – 2
–2x – 2
x2 + x
Finally, we add:
x + 1
x – 2
–2x – 2
x2 + x
x2 – x – 2
A “Harder” Example
One of the nicest things about this method of multiplying polynomials is that it can be used to multiply ANY two polynomials together (not just binomials). For example, let’s multiply the trinomials x2 + 2x – 1 and 2x2 – x + 3 together.
x2 + 2x – 1
2x2 – x + 3
3x2 + 6x – 3
–x3 – 2x2 + x
2x4 + 4x3 – 2x2
2x4 + 3x3 – x2 + 7x – 3
Summary and Further Exploration
To summarize, the algorithm I illustrated in this post is better than FOILING for the following reasons:
- This method works for multiplying ANY two polynomials together, whereas FOIL works ONLY for binomials.
- Everyone already essentially knows this algorithm from elementary school.
- It is much easier to see WHY this algorithm works. I’m going to leave the “why” as an exercise.
Let me leave you a few problems to practice on your own as well as some theoretical questions.
Exercises
- Multiply the polynomials 3x4 + 5x3 – x2 + x – 1 and 2x3 – 3x2 + x – 4.
- Explain why the algorithm presented here works. In particular, how is the distributive property being used?
- Show that FOIL is equivalent to the distributive property.
- Why is FIOL more efficient than FOIL? In other words which property of the real numbers do you need to FOIL that you DO NOT need to FIOL?
If you think your friends would like this article, please share:
See you next week…
Challenging Math Questions
Last week I gave you some challenging math questions to work on. Click the following link to see last week’s post: Some Challenging Mathematics To Raise Mathematical Maturity
Today I will provide solutions to each of those questions.
Warm-up Exercises
Recall that a set B is a subset of a set A if every element of B is an element of A. For example, if A = {1,2,3,4,5,6} and B = {4,5,6}, then B is a subset of A. Also { } is the emptyset, the unique set consisting of no elements.
- How many subsets does { } have? List them.
{ } is a subset of every set. In particular, { } is a subset of itself. This is the only subset of { }. So { } has 1 subset, namely { }. (Note that 1 = 20)
- How many subsets does {1} have? List them.
{1} has 2 subsets: { } and {1}. (Note that 2 = 21)
- List the subsets of {1, 2}, {1, 2, 3}, and {1, 2, 3, 4}.
{1, 2} has 4 subsets. They are { } , {1}, {2}, and {1,2}. (Note that 4 = 22)
{1, 2, 3} has 8 subsets: { } , {1}, {2}, {1,2}, {3}, {1,3}, {2,3}, and {1,2,3}. (Note that 8 = 23)
{1, 2, 3, 4} has 16 subsets: { } , {1}, {2}, {1,2}, {3}, {1,3}, {2,3}, {1,2,3}, {4}, {1,4}, {2,4}, {1,2,4}, {3,4}, {1,3,4}, {2,3,4}, and {1,2,3, 4}. (Note that 16 = 24)
- How many subsets does the set {1, 2, 3, 4, 5, 6, 7, 8} have?
Following the pattern in the previous examples {1, 2, 3, 4, 5, 6, 7, 8} has 28 = 256 subsets.
- How many subsets does the set {1,…, n} have where n is a positive integer.
{1,…,n} has 2n subsets.
Theoretical Exercise
- Give a proof of the result from problem 5.
Solution by Mathematical Induction: The base case is problem 1. For the inductive step, suppose that every set A with k elements has 2k subsets. Let B be a set with k+1 elements, and let x be any element of B. By assumption there are 2k subsets of B that do not contain x, and 2n subsets of B that do contain x, for a total of 2k+ 2k = 2(2k) = 2k+1 subsets. By the Principle of Mathematical Induction {1,…,n} has 2n subsets for all integers n ≥ 0.
Remarks:
(i) The Principle of Mathematical Induction says that if a statement is true for n = 0, and the truth of the statement for k implies the truth for k + 1, then the statement is true for all integers n ≥ 0.
(ii) Note that the lists chosen in problems 2 and 3 emulate the proof given here.
Solution by counting: There are nCk subsets of {1,…, n} with k elements. So all together there are nC0 + nC1 +…+ nCn= (1 + 1)n = 2n subsets of {1,…, n}.
Remarks:
(i) nCk means the number of combinations of n things taken k at a time. In a combination order does not matter (as opposed to the permutation nPk where the order does matter).
nCk = n!/[k!(n – k)!]
We don’t actually need to do any of these computations for this problem.
(ii) Here we have used the Binomial Theorem with x = y = 1:
(x + y)n = nC0 xny0 + nC1 xn-1y1 +…+ nCn-1 x1yn-1 + nCn x0yn
(1 + 1)n = nC0 1n10 + nC1 1n-111 +…+ nCn-1 111n-1 + nCn 101n
2n = nC0 + nC1 +…+ nCn-1 + nCn
Advanced Exercises
Recall that a set is selfish if the number of elements it has is in the set. For example, X10 = {1,2,3,4,5,6,7,8,9,10} is selfish because it has 10 elements, and 10 is in the set. A selfish set is minimal if none of its proper subsets is also selfish. For example, the set X10 is not a minimal selfish set because {1} is a selfish subset. Let Xn = {1,…,n}.
- How many selfish subsets does Xn have where n is a positive integer?
Let’s start with some simple examples.
X1 = {1} has 1 selfish subset, namely {1} itself.
The selfish subsets of X2 = {1,2} are {1} and {1,2}, so that X2 has 2 selfish subsets.
The selfish subsets of X3 = {1,2,3} are {1}, {1,2}, {2,3}, and {1,2,3}, so that X3 has 4 selfish subsets.
The selfish subsets of X4 = {1,2,3,4} are {1}, {1,2}, {2,3}, {1,2,3}, {2,4}, {1,3,4}, {2,3,4} and {1,2,3,4}, so that X4 has 8 selfish subsets.
In general, it looks like Xn has 2n-1 selfish subsets.
To see this, note that there are n-1Ck-1 selfish subsets of {1,…,n} with k elements (we must choose k, and then we choose k – 1 elements from the remaining n – 1 elements). So all together there are
n-1C0 + n-1C1 +…+ n-1Cn-1 = (1 + 1)n-1 = 2n-1
selfish subsets of {1,…,n}.
- List the minimal selfish subsets of Xn for n = 1, 2, 3, 4, 5, and 6.
X1 has 1 minimal selfish subset, namely {1}.
X2 has 1 minimal selfish subsets, namely {1}. (Note that {1,2} is selfish, but not minimal because {1} is a selfish subset.)
X3 has 2 minimal selfish subsets, namely { 1} and {2,3}.
X4 has 3 minimal selfish subsets, namely {1}, {2,3}, and {2,4}.
X5 has 5 minimal selfish subsets. They are {1}, {2,3}, {2,4}, {2,5}, and {3,4,5}.
X6 has 8 minimal selfish subsets. They are {1}, {2,3}, {2,4}, {2,5}, {3,4,5}, {2,6}, {3,4,6}, and {3,5,6}.
- How many minimal selfish subsets does X10 have?
Following the pattern, it looks like X7 has 8 + 5 = 13 minimal selfish subsets, X8 has 13 + 8 = 21, X9 has 21 + 13 = 34, and X10 has 34 + 21 = 55 minimal selfish subsets.
- In terms of n, how many minimal selfish subsets does the set Xn have?
Xn has fn minimal selfish subsets where fn is the nth term of the Fibonacci sequence.
Remark: The Fibonacci sequence is the sequence
fn = fn-1 + fn-2, f1 = f2 = 1.
The first few terms of the Fibonacci sequence are
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
- Give a proof of the result from problem 10.
We will prove this by the Principle of Strong Induction on n, with the base case of n = 1 and n = 2 already complete. Assume that k > 2 and that Xr has fr minimal selfish subsets for each r < k. Each minimal selfish subset of Xk-1 is a minimal selfish subset of Xk, and if A is a minimal selfish subset of Xk-2, then the set A’ formed by adding 1 to each element of A, and throwing in k, is a minimal selfish subset of Xk. This yields fk-1 + fk-2 = fk minimal selfish subsets of Xk. Conversely, note that if a minimal selfish subset of Xk does not contain k, then it is a minimal selfish subset of Xk-1, and if a minimal selfish subset of Xk does contain k, then if we delete k and subtract 1 from each of the remaining elements we get a minimal selfish subset of Xk-2. Thus there are exactly fk minimal selfish subsets of Xk.
Remark: The Principle of Strong Induction says that if a statement is true for n = 0 (or more generally n = m), and the truth of the statement for all r < k implies the truth for k, then the statement is true for all integers n ≥ 0 (or more generally n ≥ m).
If you liked this article, please share it with your Facebook friends:
Mathematical Maturity
I like to define mathematical maturity as “one’s ability to analyze, understand, and communicate mathematics.” Students with higher levels of mathematical maturity are more likely to perform well on standardized math tests. For more information about mathematical maturity, click on the following link: Mathematical Maturity
Challenging Mathematics
Today I would like to challenge you a bit while helping you take some steps toward increasing your level of mathematical maturity by presenting you with some more difficult mathematics. Solutions to the questions below will be provided in next week’s blog post, but please post your solutions or partial solutions in the comments below.
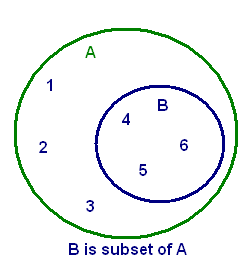Basic Definition
The first few questions will use the following definition: B is a subset of a set A if every element of B is an element of A. For example, if A = {1,2,3,4,5,6} and B = {4,5,6}, then B is a subset of A.
As another example, if C = {a,b}, then all of the subsets of C are { }, {a}, {b}, and {a,b} (here { } is the emptyset, the unique set consisting of no elements).
Warm-up Exercises
- How many subsets does { } have? List them.
- How many subsets does {1} have? List them.
- List the subsets of {1,2}, {1,2,3}, and {1,2,3,4}.
- How many subsets does the set {1,2,3,4,5,6,7,8} have?
- How many subsets does the set {1,…,n} have where n is a positive integer.
Theoretical Exercise
- Give a proof of the result from problem 5.
There are several methods that can be used for number 6. I personally prefer to use Mathematical Induction. Those of you that know this method give it a try. More information can be found at this Wikipedia page: Mathematical Induction
There are several other methods that can be used as well. Please post your attempts at this problem in the comments.
Now let’s take a look at some more advanced concepts.
Advanced Definitions
Define a set to be selfish if the number of elements it has is in the set. For example, X10 = {1,2,3,4,5,6,7,8,9,10} is selfish because it has 10 elements, and 10 is in the set. A selfish set is minimal if none of its proper subsets is also selfish. For example, the set X10 is not a minimal selfish set because {1} is a selfish subset. Let Xn = {1,…,n}.
Advanced Exercises
- How many selfish subsets does Xn have where n is a positive integer?
- List the minimal selfish subsets of Xn for n = 1, 2, 3, 4, 5, and 6.
- How many minimal selfish subsets does X10 have?
- In terms of n, how many minimal selfish subsets does the set Xn have?
- Give a proof of the result from problem 10.
If you liked this article, please share it with your Facebook friends:
Once again solutions will be provided next week.
Strategy Map To The Blue Book
Students have been asking me lately if I have compiled a list of Blue Book problems that coordinates with each of the strategies I teach? For example if a student wants to practice the strategy of picking numbers they would like to see a list of blue book problems where this strategy can be used.
I am happy to report that I have finally made such a list available. This Strategy Map to the Blue Book is now available free of charge to anyone who would like a copy. In fact, simply click the picture of the front cover above to begin your free download.
The strategies listed in this compilation are all found in The 32 Most Effective SAT Math Strategies.
A Few Notes
After each strategy in this manuscript is a list of problems from the tests in the 2nd edition of the College Board’s Official Study Guide. Each problem is listed as X:Y:Z where X is the test number, Y is the section number and Z is the question number. For example 4:3:17 means Blue Book test 4, section 3, question 17.
Here are a few things worth noting:
- The number of problems associated with a given strategy gives a general guideline as to how often that strategy can be used on the SAT.
- This correlation is not exact. For example I would not say that strategy 16 can be used more frequently than strategy 15 just because there is 1 more Blue Book problem associated with it.
- Some strategies have no problems associated with them. All that this means is that there are no such problems in the Blue Book. These strategies were all developed using information from SATs given over the last 10 years. So you may or may not see problems on the SAT you take where these particular strategies can be used.
- If you see anything missing from this list or something that is mislabeled please let me know: steve@SATPrepGet800.com
Get 800 SAT Math Prep Books
Click the picture below for a complete list of my SAT math prep books:
As always feel free to post any questions you have on my Facebook wall:
Solutions To Last Week’s Hard SAT Math Geometry Problems
Welcome back everybody. Today I would like to post the solutions to the three hard SAT math geometry questions I posted last week. Please feel free to post your own solutions or attempted solutions in the comments below as well. If you still want further explanation after reading the below solutions please do not hesitate to ask – you can use the comments section below for this as well.
Problems With Solutions
- The lengths of the sides of a triangle are x, 16 and 31, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?
Solution: By the triangle rule, x lies between 31 – 16 = 15 and 31 + 16 = 47. That is, we have 15 < x < 47. But we are also given that x is the length of the shortest side of the triangle. So x < 16.Therefore we can grid in any number between 15 and 16. For example, we can grid in 15.1.
For more information on the triangle rule see the following article: The Triangle Rule
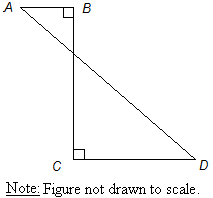
- In the figure above, if AB = 4, BC = 24, and AD = 26, then CD =
Solution: The problem becomes much simpler if we “move” BC to the left and AB to the bottom as shown below.
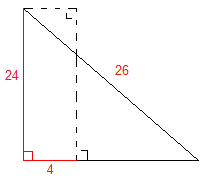
We now have a single right triangle and we can either use the Pythagorean Theorem, or better yet notice that 26 = (13)(2) and 24 = (12)(2). Thus the other leg of the triangle is (5)(2) = 10. So we see that CD must have length 10 – 4 = 6.
Remark: If we didn’t notice that this was a multiple of a 5-12-13 triangle, then we would use the Pythagorean Theorem as follows.
(x + 4)2 + 242 = 262
(x + 4)2 + 576 = 676
(x + 4)2 = 100
x + 4 = 10
x = 6
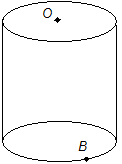
- The figure above shows a right circular cylinder with diameter 6 and height 9. If point O is the center of the top of the cylinder and B lies on the circumference of the bottom of the cylinder, what is the straight-line distance between O and B?
Solution: We draw a right triangle inside the cylinder as follows:
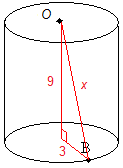
Note that the bottom leg of the triangle is equal to the radius of the circle (not the diameter) which is why it is 3 and not 6. We can now use the Pythagorean Theorem to find x.
x2 = 32 + 92 = 9 + 81 = 90
Taking the square root gives x approximately equal to 9.4868. So we grid in 9.48 or 9.49.
More Hard SAT Math Practice Problems
For many more hard SAT math problems like these, each with several fully explained solutions, check out the Advanced Course from my 28 SAT Math Lessons Series. Click on the picture below for more information about this book.
If you think your friends would like these problems, please share:
And if you have any questions on this topic, then please post them on my Facebook wall:
See you next week…
Level 5 SAT Geometry Problems
- The lengths of the sides of a triangle are x, 16 and 31, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?
- In the figure above, if AB = 4, BC = 24, and AD = 26, then CD =
- The figure above shows a right circular cylinder with diameter 6 and height 9. If point O is the center of the top of the cylinder and B lies on the circumference of the bottom of the cylinder, what is the straight-line distance between O and B?
More Hard SAT Math Practice Problems
For many more hard SAT math problems like these, each with several fully explained solutions, check out the Advanced Course from my 28 SAT Math Lessons Series. Click on the picture below for more information about this book.
If you think your friends would like to try these problems, please share:
And if you have any questions on this topic, then please post them on my Facebook wall:
I will answer your questions right away.
Speak to you soon!
Learning Math Or Strategy
There is a lot of information out there for SAT math preparation. Some of it is good, some of it is bad, and different sources often lead to viewpoints which contradict each other. Some SAT prep tutors suggest that students should focus on learning SAT math strategies while others insist that students need to spend time learning or reviewing mathematical concepts. The College Board themselves preach that students shouldn’t even prepare for the exam – they should just focus on their schoolwork and SAT score improvement will be a natural side effect.
The perfect situation, of course, would be to do both – learn the strategies and learn the math. Any student that is an expert in the math being tested and knows all of the important SAT specific strategies will certainly get an 800 in math. The problem is that for many students this is just too much. Trying to learn too much may lead to frustration, feelings of being overwhelmed, and an overall reduction in confidence. The end result may actually be lower SAT scores and this is certainly not what any of us want.
Algebra Or Not?
As a simple example, most of the students I work with have much weaker algebra skills than I would like. So the question is “should I spend a large amount of time reviewing algebra during SAT classes?” And my answer is a definitive “no!” Students have had many opportunities to learn algebra in their high school classes. They have already been exposed to it many, many times. Why am I going to spend even more time beating a dead horse? In most SAT math problems algebra can be avoided completely. So instead of repeating the same unsuccessful process I’m going to approach the situation from a different direction entirely.
Let me just make it clear that I do not completely discourage students from solving SAT math problems algebraically. If a student has exceptional algebra skills, then by all means they can use them when solving problems. I usually even demonstrate algebraic solutions to most students for many SAT problems. But while going over algebraic solutions I keep my expectations very low. Although I think students should see certain problems solved algebraically, I do not get disappointed if they cannot reproduce those solutions. After all, I am giving them a whole other list of alternatives to solving problems without using algebra.
Let me also emphasize that I like for all of my students to learn as many strategies as possible. Even if a student can solve many SAT math problems algebraically I like them to learn alternative methods because eventually they will come across a problem where the algebra is just too tricky for them. And sometimes, no matter how good a student’s algebra skills are, a strategy will result in arriving at a solution faster.
What About Basic Concepts?
Now let’s get even more basic for a moment. Should time be taken out to review really basic mathematical concepts? My answer again is “no.”
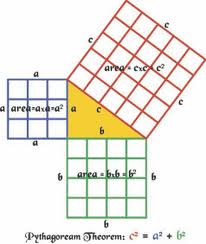
No I am not implying that every single student knows the Pythagorean Theorem. But even if they do not it is not a big deal. If a student is trying to do a problem where the Pythagorean Theorem is needed, and they cannot apply the theorem correctly, then it is easy enough to fill in that small gap in knowledge at that time.
When preparing for the SAT I strongly recommend that some emphasis is placed on strategy. In particular for low to mid scoring students most of their preparation should focus on strategy. Higher scoring students (over 600) should balance their time between learning strategies and reviewing more advanced mathematical concepts.
Where To Find All These SAT Math Strategies
All of the strategies you need to know can be found in my 28 SAT Math Lessons Series. But these are not just strategy guides. Each one contains hundreds of practice problems with solutions, and the mathematics is all there too. Click on the picture below for more information about these books.
If you liked this article, please share it with your Facebook friends:
And if you have any questions on this topic, then please post them on my Facebook wall:
Speak to you soon!
Informal Algebra
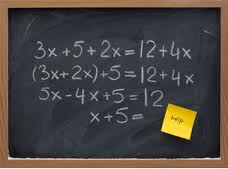
Suppose we are asked to solve for x in the following equation:
x + 3 = 8
In other words, we are being asked for a number such that when we add 3 to that number we get 8. It is not too hard to see that 5 + 3 = 8, so that x = 5.
I call the technique above solving this equation informally. In other words, when we solve algebraic equations informally we are solving for the variable very quickly in our heads. I sometimes call this performing “mental math.”
Algebra The Formal Way
We can also solve for x formally by subtracting 3 from each side of the equation:
x + 3 = 8
-3 -3
x = 5
In other words, when we solve an algebraic equation formally we are writing out all the steps – just as we would do it on a test in school.
To save time on the SAT you should practice solving equations informally as much as possible. And although informal skills should take precedence during your SAT prep, you should also practice solving equations formally – this will increase your mathematical skill level.
Another Example
Let’s try another one:
5x = 30
Informally, 5 times 6 is 30, so we see that x = 6.
Formally, we can divide each side of the equation by 5:
5x = 30
5 5
x = 6
A Harder Example
Now let’s get a little harder:
5x + 3 = 48
We can still do this informally. First let’s figure out what number plus 3 is 48. Well, 45 plus 3 is 48. So 5x is 45. So x must be 9.
Here is the formal solution:
5x + 3 = 48
-3 -3
5x = 45
5 5
x = 9
Exercise
Try this one on your own: 3x + 4 = 31
And feel free to post your explanations in the comments.
If you liked this article, please share it with your Facebook friends:
I’ll see you next week…
This is a group for SAT and ACT math prep experts, tutors, and authors, and high school math teachers and administrators interested in their students’ SAT and ACT math preparation. You must apply for membership – this is strictly a group for educators.
We will be discussing teaching methods, important strategies and concepts, how we teach students of different score levels, and how to implement effective test prep courses into our high schools.
Each week I will be posting a new topic for discussion, but group members are welcome to post their own topics as well as long as they are relevant to the group.
Note that spam, self-promotion and sales pitches are not allowed and this policy will be strictly enforced.
Please feel free to share this page with other test prep professionals that you know.
I look forward to discussing SAT and ACT math preparation with you.
I’ll see you on LinkedIn!
SAT/ACT Math Prep Professionals
Today I would just like to let everyone know that I have made sample chapters available for each of my SAT and ACT math prep books. So please, try out a lesson, learn some strategies, and carefully review my teaching style before you decide to make a purchase.
GET 800 Free Book Samples
Click on each of the book images below to download a free preview from each book.
Please share this information with your Facebook friends:
Next week I will get back to providing you with SAT strategies that will have an immediate effect on your score. I’ll see you then!