500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Teachers and tutors may have their own personal philosophies, but there is one thing that they all agree on – every student that wants to improve their score in SAT math should be attempting the questions from the practice tests given in “The Official SAT Study Guide” by the College Board.

Despite this, my colleagues and I have always wanted more from the infamous blue book. The problems in the Official Guide are fantastic – they are exactly the types of questions you will encounter on the SAT. The explanations to the problems, however, are not so fantastic. In the blue book there are no explanations at all, and if you do have access to the College Board’s solutions then you have only a single solution which, in my opinion, may not always be the best way to solve that problem. This is why I have created “The Official SAT Study Guide Companions.”

The Official SAT Study Guide Companions contain solutions to the SATs in the Official SAT Study Guide. As usual, I give simple, efficient, in-depth solutions to each of these problems, and most problems are solved using several different methods.

I have created the guides in response to the teachers, tutors and students that have found the College Board’s solutions to these problems to be unsatisfactory.

Tests 1, 2, 3 and 4 are already available; Test 1 is available for free by subscribing to my free 12 part SAT math prep email course. If you have not subscribed to this course called the 800 Initiation, you are missing out an a great opportunity to improve your score. And Tests 2, 3 and 4 can be found here.

I have just released my solutions to Test 5, which is available as an electronic download for $3.

I’m working as quickly as I can to get the next 5 tests out for you to use – keep an eye on this space for more solutions to help you to, ultimately,  get a higher score. You can expect test 6 to be available in the next month or so.

Let’s keep in touch!

This book will guide students in a step by step fashion to increase their SAT math scores within one month – providing the lesson schedule is adhered to.

I have created this book to provide quick results to students that want to dramatically improve their scores in a short period of time.

If you are currently scoring below 500 in SAT math and you wish to get to the next score level quickly and efficiently, then this new book is for you.

When this book is used by students for self study a significant rise in SAT math score will result as long as each lesson is completed and the content is internalized.

The Intermediate and Advanced versions of this book are already available, but this book is specifically designed for students that are currently scoring below 500 in SAT/PSAT Math.

After the lessons have been completed, I believe a student should get closer to a score of 600.

This book is perfect for those students that only have a limited time for study. It takes all the guesswork out of what to study. If you are familiar with my work, you know that I am extremely thorough with the solutions to problems I provide as practice. My years of experience have enabled me to create this guide that will take you to a higher SAT math score.

Click on this link to take you to the product page – you can buy an electronic or paperback version of the book for a limited time only. The electronic version of this book is only $5.

That’s right, only $5!! The usual price is $24 dollars for the electronic version, so be quick with your purchase…

Picking Numbers In Percent Problems

Last week we looked at the basic but important strategy of picking numbers. Click the following link to view that post: Picking Numbers – A Basic SAT Math Strategy

At the end of that post, I did say that we would be applying this strategy to percent problems.

When picking a number in percent problems, the best choice is usually the number 100. After all, the word percent literally translates to “out of 100.”

Example 1:

Let’s take a look at an SAT problem involving percents:

There are b bricks that need to be stacked. After k of them have been stacked, then in terms of b and k, what percent of the bricks have not yet been stacked?

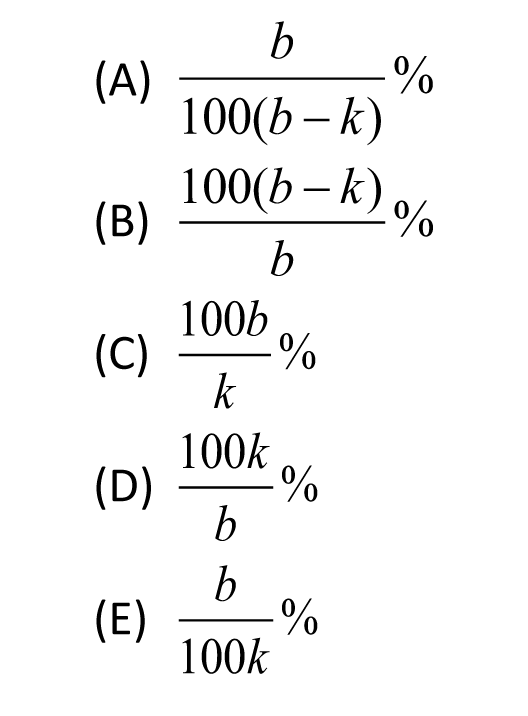
Since this is a percent problem let’s choose 100 for the total number of bricks. So we have b = 100. For k, let’s choose 25, so that 25 bricks have been stacked, and so that means 100 – 25 = 75 have not been stacked. Since we started with 100 as our total, 75% of the bricks have not been stacked. Remember to put a big, dark circle around 75%. We make the substitutions b = 100 and k = 25 into each answer choice.

 

We now compare each of these percents to the percent that we put a nice big, dark circle around. Since (A), (C), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice (B).

As I always like to stress: (B) is not the correct answer simply because it is equal to 75%. It is correct because all four of the other choices are not 75%. You absolutely must check all five choices!

Example 2:

Now let’s look at a percent problem without answer choices. Even though there is no variable in the problem to pick a number for, we can still use the number 100 to solve the problem quickly and easily.

If Matt’s weight increased by 30 percent and Lisa’s weight decreased by 20 percent during a certain year, the ratio of Matt’s weight to Lisa’s weight at the end of the year was how many times the ratio at the beginning of the year?

Again, 100 is the magic number – let’s choose 100 pounds for both Matt’s weight and Lisa’s weight at the beginning of the year. Matt’s weight at the end of the year was then 100 + 30 = 130 pounds and Lisa’s weight at the end of the year was 100 – 20 = 80 pounds. We then have that the ratio of Matt’s weight to Lisa’s weight at the beginning of the year was 100/100 = 1, and the ratio of Matt’s weight to Lisa’s weight at the end of the year was 130/80 = 13/8. We can therefore grid in 13/8.

Side note: 13/8 is equal to 1.625 as a decimal. Thus, we can also grid in 1.62 or 1.63. We get 1.62 by truncating the decimal, and 1.63 by rounding the decimal. Truncating is better because less thought is involved. Note that if you grid in 1.6 the answer will be marked wrong.

So remember the magic number ‘100’ whenever you see a problem with the word “percent” in it… but as always, practice makes perfect – so find more of these problems, such as those found in my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Picking Numbers

The strategy of “picking numbers” works on a wide range of different SAT math problems in all topics and difficulty levels. It can often be used to make a difficult problem much easier to understand, and if you are careful in its use, you will usually get the answer without too much trouble. The idea is simple – replace the unknowns in the problem with specific values.

Here are some guidelines when picking numbers.

1. Pick a number that is simple but not too simple. In general you might want to avoid picking 0 or 1 (but 2 is usually a good choice).
2. Try to avoid picking numbers that appear in the problem.
3. When picking two or more numbers try to make them all different.
4. Most of the time picking numbers only allows you to eliminate answer choices. So do not just choose the first answer choice that comes out to the correct answer. If multiple answers come out correct you need to pick a new number and start again. But you only have to check the answer choices that have not yet been eliminated.
5. If there are fractions in the question a good choice might be the least common denominator (lcd) or a multiple of the lcd.
6. In percent problems choose the number 100.
7. Do not pick a negative number as a possible answer to a grid-in question. This is a waste of time since you cannot grid a negative number.
8. If your first attempt does not eliminate 4 of the 5 choices, try to choose a number that is of a different “type.” Here are some examples of types:
   1. A positive integer greater than 1.
   2. A positive fraction (or decimal) between 0 and 1.
   3. A negative integer less than -1.
   4. A negative fraction (or decimal) between -1 and 0.
9. If you are picking pairs of numbers try different combinations from (8). For example you can try two positive integers greater than 1, two negative integers less than -1, or one positive and one negative integer, etc.

Remember that these are just guidelines and there may be rare occasions where you might break these rules. For example sometimes it is so quick and easy to plug in 0 and/or 1 that you might do this even though only some of the answer choices get eliminated.

Examples

Okay, so let’s try solving an SAT math practice problem by picking numbers:

1. For nonzero numbers a, b, and c, if c is three times b and b is 1/5 of a, what is the ratio of a² to c²?
               (A)   9 to 25
               (B)   25 to 9
               (C)   5 to 9
               (D)   5 to 3
               (E)   3 to 5

Looks scary? This SAT problem is actually pretty easy if you pick numbers.

Let’s choose a value for a, say a = 5. Then b = 1, c = 3, and therefore the ratio of a² to c² is 25 to 9, choice (B).

Simple, right? Maybe a bit too simple? You can of course solve this SAT math problem algebraically as well, but an algebraic solution is more likely to lead to careless errors, and in this problem will actually take more time than picking numbers.

Here is one more  SAT math problem for more practice:

2. If a = 3^b and b = c + 4 , what is a/27 in terms of c?
               (A)   c + 1
               (B)   3^c
               (C)   3^c+1
               (D)   3^c + 1
               (E)   3^c + 2

Using the same method as above, let’s pick a number for c, say c = 2. It follows that b = 2 + 4 = 6. So using our calculator, a = 3⁶ = 729. We then have a/27 = 729/27 = 27. Put a nice big, dark circle around this number so that you can find it easily later. We now substitute a 2 for c into each answer choice and use our calculator.

We now compare each of these numbers to the number that we put a nice big, dark circle around. Since (A), (B), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice (C).

Remember by picking a number, we can only eliminate answer choices: (C) is not the correct answer simply because it is equal to 27. It is correct because all four of the other choices are not 27. You absolutely must check all five choices!

You can see how powerful picking numbers can be to solve SAT math problems. Follow the guidelines I have provided above and you should be solving more difficult SAT math problems with ease. In next week’s post we will see how to apply the strategy of picking numbers to problems involving percents. Click the following link to view that post: Picking A Number To Solve Percent Problems

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Until then…

Welcome to this week’s message. I hope you have found what I have to say regarding the SAT useful…

Students often ask me if there is any way they will ever be able to get through all of the SAT math questions in the given amount of time. In response, I always explain they are asking the wrong question. For most students, worrying about getting to the end of the test will not improve your score. Of course, if you are shooting for an 800, it goes without saying that you need to attempt and correctly solve every problem on SAT day (although there are rare instances, once every few years, in which there is an SAT where you can miss one math problem and still score an 800).

For most students, the problem is that they are already attempting too many questions. This advice might sound strange at first because students have been conditioned not to leave questions blank on tests. But the fact is, on a standardized test, students will usually increase their score by reducing the number of questions that they attempt.

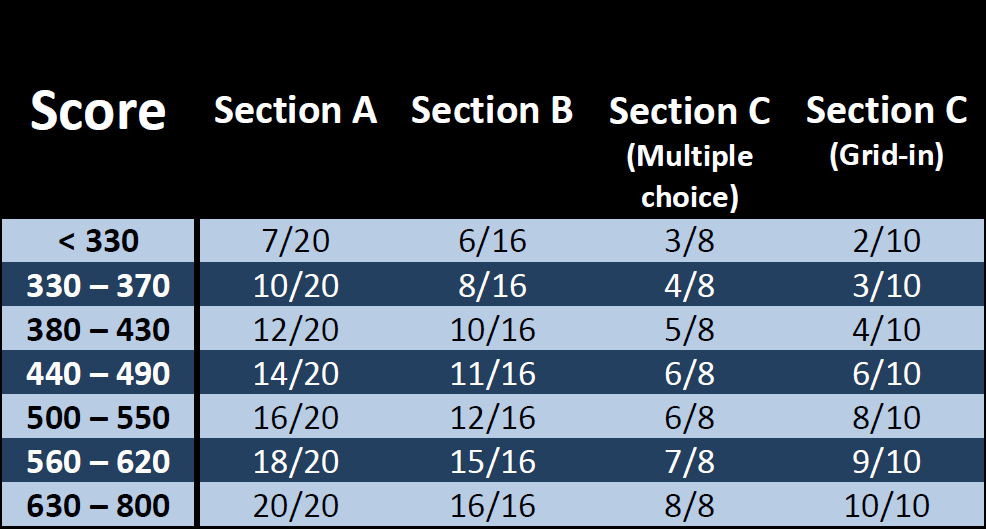
First, let’s have a quick overview of the math section on the SAT: There are 3 math sections on the SAT. They can appear in any order. There is a 20 question multiple choice section, a 16 question multiple choice section, and an 18 question section that has 8 multiple choice questions and 10 gridins.

Let’s call these sections A, B, and C, respectively. You should first make sure that you know what you got on your last SAT practice test, actual SAT, or actual PSAT (whichever you took last). The table below shows the general goal (number of problems to attempt) you should go for when taking the exam.

For example, a student with a current score of 450 should attempt the first 14 questions from section A, the first 11 questions from section B, the first 5 multiple choice questions from section C, and the first 6 gridins from section C.

This is just a general guideline. Of course it can be fine tuned. As a simple example, if you are particularly strong at number theory problems, but very weak at geometry problems, then you may want to try every number theory problem no matter where it appears, and you may want to reduce the number of geometry problems you attempt.

Here is the video on YouTube that explains how many questions you should be answering.

 

Let’s keep in touch!

 

Last week I described a very simple yet effective strategy to solve certain SAT math problems.

The strategy of “taking a guess” is a very useful way to avoid complicated algebra and ensure that a question is answered correctly. See the post from last week for details if you have not already been exposed to this strategy: Basic SAT Math Strategy – Take A Guess

Example

Let’s take a look at another example of how this strategy can be used effectively. Here is a more difficult problem for you to chew the end of your pencil over:

Let the function f be defined for all values of x by f(x) = x(x + 1). If k is a positive number and f(k + 5) = 72, what is the value of k?

Looks tricky?

Well let’s see how we can solve this tricky problem quickly by “taking a guess.”

Let’s take a guess for k, say k = 2. Then we have f(2 + 5) = f(7) = (7)(8) = 56. This is too small. So let’s guess that k = 3 next. Then f(3 + 5) = f(8) = (8)(9) = 72 which is correct. So the answer is 3.

Algebraic Solution

You can see that by using the method of guessing we have found the answer very quickly. Let’s compare this to solving the problem algebraically. Do not worry if the solution that follows confuses you. You will never have to use this method on an actual SAT if you choose not to.

f(k + 5) = (k + 5)(k + 6) = k² + 11k + 30.

Since f(k + 5) = 72, we have k² + 11k + 30 = 72. Subtracting 72 from each side of this equation yields

k² + 11k – 42 = 0
(k – 3)(k + 14) = 0

So k = 3 or k = -14. We reject the negative solution because the question says that k is positive. Therefore the answer is 3.

Further Discussion

As you can see, the algebraic solution involves a fairly complicated multiplication which leads to a quadratic equation. The simplest way to solve this quadratic equation is by bringing everything over to one side and factoring. We can see that the answer is obtained correctly, but for most students there is a danger of getting lost in the algebra. This method also takes longer than the method of taking a guess. So for these reasons, why would you want to use algebra to solve a problem such as the example above? Knowing how the algebra works, however, is good for gaining mathematical maturity. This is certainly important if you want to get an 800 in SAT math. So if you are going for a perfect score, practice the algebraic solution at home. Just do not use it on test day!

More Practice

If you have any questions or comments regarding this strategy, please do let me know. And if you want more practice with this particular strategy, as well as the other important strategies you need to know to improve your SAT math score, please check out my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

Look out for more of my SAT math strategies, hints and tips next week!

Taking A Guess

This week I would like to discuss another very basic math strategy for standardized tests such as the ACT and SAT. This strategy is extremely simple to apply and it will often allow you to avoid messy algebraic computations. I call this strategy “Take a Guess.”

Sometimes the answer choices themselves cannot be substituted in for the unknown or unknowns in the problem. But that doesn’t mean you can’t guess your own numbers. Try to make as reasonable a guess as possible, but don’t over think it. Keep trying until you zero in on the correct value.

Example

Let’s see this simple technique in action  with an appropriate math problem.

Bill has cows, pigs and chickens on his farm. The number of chickens he has is three times the number of pigs, and the number of pigs he has is 2 more than the number of cows. Which of the following could be the total number of these animals?

(A)   14
(B)   15
(C)   16
(D)   17
(E)   18

Let’s take a guess and say that Bill has 3 cows. He then has 3 + 2 = 5 pigs, and also 3·5 = 15 chickens. So the total number of animals is 3 + 5 + 15 = 23. This is too big. So let’s guess lower and say that Bill has 1 cow. Then he has 1 + 2 = 3 pigs, and 3·3 = 9 chickens. It follows that the total number of animals is 1 + 3 + 9 = 13, too small. So Bill must have 2 cows, 2 + 2 = 4 pigs, and 3·4 = 12 chickens. Thus, the total we get is 2 + 4 + 12 = 18 animals. So the answer is choice (E).

Teachers and tutors may have their own personal philosophies, but there is one thing that they all agree on – every student should be attempting the questions from the practice SATs given in “The Official SAT Study Guide.”

Despite this, my colleagues and I have always wanted more from the infamous blue book. The problems in the Official Guide are fantastic – they are exactly the types of questions you will encounter on the SAT. The explanations to the problems, however, are not so fantastic. In the blue book there are no explanations at all, and if you do have access to the College Board’s solutions then you have only a single solution which, in my opinion, may not always be the best way to solve that problem. This is why I have created “The Official SAT Study Guide Companions.”

The Official SAT Study Guide Companions contain solutions to the SATs in the Official SAT Study Guide. As usual, I give simple, efficient, in-depth solutions to each of these problems, and most problems are solved using several different methods.

I have created the guides in response to the teachers, tutors and students that have found the College Board’s solutions to these problems to be unsatisfactory.

Tests 1 and 2 are already available; Test 1 is available for free by subscribing to my free 12 part SAT math prep email course. And Test 2 can be found here.

I have just released my solutions to Tests 3 and 4, which are available as electronic downloads for $3 each.

I’m working as quickly as I can to get the next six tests out for you to use – keep an eye on this space for more solutions.

This is the third video in my series of me completing all of the math sections from an SAT.

Take a look at my previous blog entries here and here to see me complete sections 3 and 7 from this SAT.

Click on play below to watch the video.

As always, feel free to comment

I have had many questions asking why my new book series 28 SAT Math Lessons To Improve Your Score In One Month is any different from my other books and any different from the SAT prep books written by big name test prep companies.

Well, this course is specifically designed to get an increase in SAT math from your current score level to the next score level. And this is why there will be three books in the series: Advanced for those scoring above 600 and want to get 800, Intermediate for those scoring between 500 – 600, and the yet to be written Beginner for those scoring below 500.

My previous blog post on describing what the Advanced book is all about can be found here.

But if you really do not want to read when you can watch, then click the play button below to see me explain how the 28 SAT Math Lessons series is different form other SAT math prep books and also to find out who these books are designed for.