500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

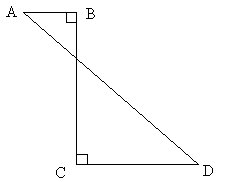
Geometry Question with Solution

Yesterday I went over a method for solving certain geometry problems by moving the sides of a figure around. You can see that post here: Moving the Sides of a Figure Around

Today I would like to solve yesterday’s problem.

Problem: In the figure below, AB = 2, BC = 8, and AD = 10. What is the length of line segment CD ?

Solution: The problem becomes much simpler if we “move” BC to the left and AB to the bottom as shown below.

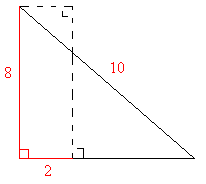
We now have a single right triangle and we can either use the Pythagorean Theorem, or better yet notice that 10 = 5 ⋅ 2 and 8 = 4 ⋅ 2. Thus, the other leg of the triangle is 3 ⋅ 2 = 6. So we see that CD must have length 6 – 2 = 4.

Remark: If we didn’t notice that this was a multiple of a 3-4-5 triangle, then we would use the Pythagorean Theorem as follows.

(x + 2)² + 8² = 10²
(x + 2)² + 64 = 100
(x + 2)² = 36
x + 2 = 6
x = 4

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Geometry Strategy – Moving the Sides of a Figure Around

Today I would like to teach you a more advanced geometry strategy that can sometimes be used on standardized tests such as the ACT, SAT, and GRE.

A seemingly difficult geometry problem can sometimes be made much easier by moving the sides of the figure around.

This procedure is best understood with an example:

Example: What is the perimeter, in meters, of the figure below?

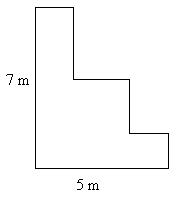
Try to solve the problem yourself before checking the solution below.

Solution: Recall that to compute the perimeter of the figure we need to add up the lengths of all 8 line segments in the figure. We “move” the two smaller horizontal segments up and the two smaller vertical segments to the right as shown below.

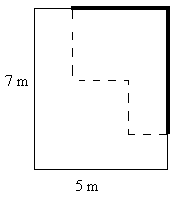
Note that the “bold” length is equal to the “dashed” length. Thus, the perimeter is

(2)(7) + (2)(5) = 14 + 10 = 24.

Warning: Although lengths remain unchanged by moving line segments around, areas will be changed. This method should not be used in problems involving areas.

Here is one more problem for you to try. See if you can find the best way to move the sides of the figure around to make the problem easy to solve. I will provide a solution to this problem tomorrow.

Example: In the figure below, AB = 2, BC = 8, and AD = 10. What is the length of line segment CD ?

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Ratio Question 3 with Solutions

Earlier this week I went over my method for setting up a ratio, and I gave you three ratio problems to try on your own. You can see that post here: Setting Up a Ratio

Today I would like to give a solution to the third of those three ratio problems. You can see solutions for the first and second problems here: Ratio Q1 Ratio Q2

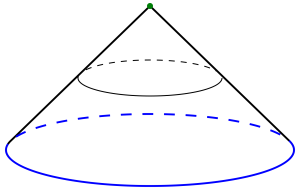
Problem 3: The height of a solid cone is 22 centimeters and the radius of the base is 15 centimeters. A cut parallel to the circular base is made completely through the cone so that one of the two resulting solids is a smaller cone. If the radius of the base of the small cone is 5 centimeters, what is the height of the small cone, in centimeters?

For those students that are getting the hang of this, here’s the quick computation right away:

Quick solution:  (22/15) ⋅ 5 = 22/3.

And here are the details for the rest of us:

Detailed solution. A picture of the problem looks like this:

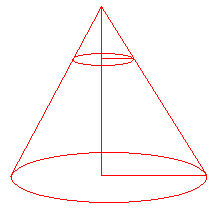
In the above picture we have the original cone together with a cut forming a smaller cone. We have also drawn two triangles that represent the 2 dimensional cross sections of the 2 cones. Let’s isolate the triangles:

The two triangles formed are similar, and so the ratios of their sides are equal. We identify the 2 key words “height” and “radius.”

 height            22       h
radius             15      5

We now find h by cross multiplying and dividing.

22/15 = h/5
110 = 15h
h = 110/15 = 22/3

 

Definition: Two triangles are similar if they have the same angles.

Notes: (1) To show that two triangles are similar we need only show that two angles of one of the triangles are equal to two angles of the other triangle (the third is free because all triangles have 180 degrees).

(2) Similar triangles do not have to be the same size.

(3) Similar triangles have sides that are all in the same proportion.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Ratio Question 2 with Solutions

Earlier in the week I went over my method for setting up a ratio, and I gave you three ratio problems to try on your own. You can see that post here: Setting Up a Ratio

Today I would like to give a solution to the second of those three ratio problems. You can see solutions for the first problem here: Ratio Question 1 with Solutions.

Problem 2: A copy machine makes 4800 copies per hour. At this rate, in how many minutes can the copy machine produce 920 copies?

Solution: We identify 2 key words. Let’s choose “copies” and “minutes.”

      copies     4800   920
    minutes     60        x

At first glance it might seem to make more sense to choose “hours” as our second key word, but choosing the word “minutes” is more efficient because

• The answer that we’re looking for must be in minutes.
• It’s extremely simple to convert 1 hour into 60 minutes.

We now find x by cross multiplying and dividing.

4800/60 = 920/x
4800x = 55200
x = 11.5

So, the answer is 11.5. ⋅

* Quick computation:  (920/4800) ⋅ 60 = 11.5.

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Ratio Question 1 with Solutions

Yesterday I went over my method for setting up a ratio, and I gave you three ratio problems to try on your own. You can see that post here: Setting Up a Ratio

Today I would like to give a solution to the first of those three ratio problems. I will give solutions to the other two problems throughout this week.

Problem 1: Running at a constant speed, a cheetah traveled 200 miles in 5 hours. At this rate, how many miles did the cheetah travel in 4 hours?

Solution: As in yesterday’s problem we identify 2 key words. This time let’s choose “miles” and “hours.”

    miles           200      x
   hours             5       4

We now find x by cross multiplying and dividing.

200/5 = x/4
800 = 5x
x = 800/5 = 160.

Alternate solution: Using d = r ⋅ t (distance = rate ⋅ time), we have

200 = r ⋅ 5
r = 200/5 = 40 mph

Using d = r ⋅ t again, we have d = 40 ⋅ 4 = 160.

* Mental math: 200 miles in 5 hours is 40 miles per hour (divide 200 by 5).  Thus, the cheetah traveled 4 ⋅ 40 = 160 miles in 4 hours.

 

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Setting Up a Ratio

Today I would like to share the method I teach for solving problems involving ratios. I have a simple 4 step system.

Step 1: Identify two key words and write them down one over the other.

Step 2: Next to each of these key words write down the numbers, variables or expressions that correspond to each key word in two columns.

Step 3: Draw in 2 division symbols and an equal sign.

Step 4: Cross multiply and divide.

This procedure is best understood with a simple example:

Example: The sales tax on an $8.00 shirt is $0.60. At this rate what would be the sales tax on a $12.00 shirt?

Try to solve the problem yourself before checking the solution below.

Solution: We begin by identifying 2 key words. In this case, such a pair of key words is “shirt” and “tax.”

shirt            8        12
tax             0.60      x

Choose the words that are most helpful to you. Notice that we wrote in the shirt prices next to the word shirt, and the tax prices next to the word tax. Also notice that the tax for an $8 shirt is written under the number 8, and the (unknown) tax for a $12 shirt is written under the 12.

Now draw in the division symbols and equal sign, cross multiply and divide the corresponding ratio to find the unknown quantity x.

8/.060  =  12/x
8x = 12(0.60)
8x = 7.2
x = 0.90

So the tax on a $12 shirt is $0.90.

I’d also like to provide a quicker solution for the more advanced student.

* Mental math: If the tax on an $8.00 shirt is $0.60, then the tax on a $4.00 shirt would be $0.30 at this rate. Thus, the tax on a $12.00 shirt would be $0.90.

Here are a few more problems for you to try. Try to use my 4 step method each time. I will provide solutions to these throughout the week.

1. Running at a constant speed, a cheetah traveled 200 miles in 5 hours. At this rate, how many miles did the cheetah travel in 4 hours?

2. A copy machine makes 4800 copies per hour. At this rate, in how many minutes can the copy machine produce 920 copies?

3. The height of a solid cone is 22 centimeters and the radius of the base is 15 centimeters. A cut parallel to the circular base is made completely through the cone so that one of the two resulting solids is a smaller cone. If the radius of the base of the small cone is 5 centimeters, what is the height of the small cone, in centimeters?

More Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

 

Hard Statistics Problem with Solution

Today I would like to give a solution to yesterday’s statistics problem. Before reading the solution, you may want to review the following article: Changing Averages to Sums

Here is the problem once again, followed by a solution.

Level 5 Statistics

Suppose that the average (arithmetic mean) of a, b, and c is h, the average of b, c, and d is j, the average of c, d, and e is k, and the average of d, e, and f is m. What is the value of (a + c) – (d + f ) ?

A) h – j + k – m
B) 3(h – j + k – m)
C) 3/4 (h – j + k – m)
D) 3(h + j + k + m)
E) 3/4 (h + j + k + m)

Solution by changing averages to sums:  We have

a + b + c = 3h

b + c + d = 3j

c + d + e = 3k

d + e + f = 3m

We subtract the second equation from the first equation to get

a – d = 3h – 3j

We subtract the fourth equation from the third equation to get

c – f = 3k – 3m

We now add these last two equations to get

a – d + c – f = 3h – 3j + 3k – 3m

This is equivalent to choice B.

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Hard Statistics Problem

Today I would like to give a hard statistics problem from the book 320 SAT Math Subject Test Problems – Level 2. I will provide a full explanation for this problem tomorrow. Feel free to leave your own solutions in the comments.

Level 5 Statistics

Suppose that the average (arithmetic mean) of a, b, and c is h, the average of b, c, and d is j, the average of c, d, and e is k, and the average of d, e, and f is m. What is the value of (a + c) – (d + f ) ?

A) h – j + k – m
B) 3(h – j + k – m)
C) 3/4 (h – j + k – m)
D) 3(h + j + k + m)
E) 3/4 (h + j + k + m)

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT, ACT, or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Exponential Growth and Decay

The current version of the SAT gives problems on exponential growth and decay. Here are the basics that you should know if you want to get a perfect SAT score:

A general exponential function has the form f(t) = a(1 + r)^ct, where a = f(0) is the initial amount and r is the growth rate. If r > 0, then we have exponential growth and if r < 0 we have exponential decay.

Examples: (1) The exponential function  f(t) = 300(2)^t  can be used to model a population with a growth rate of 1 = 100% each year that begins with 300 specimens. The growth rate of 100% tells us that the population doubles each year.

(2) The exponential function  f(t) = 50(3)^2t  can be used to model a population with a growth rate of 2 = 200% every 6 months that begins with 50 specimens. The growth rate of 200% tells us that the population triples. Since c = 2, the tripling occurs every  1/2  year or 6 months.

(3) The exponential function  f(t) = 120(0.75)^t/3  can be used to model a substance which is decaying at a rate of 1 – 0.75 = 0.25 = 25% every 3 years. The initial amount of the substance might be 120 grams. Since c = 1/3, the 25% decay occurs every 3 years.

(4) A quantity that continually doubles over a fixed time period can be modeled by the exponential function f(t) = a(2)^t/d  where a is the quantity at time t = 0, and d is the doubling time in years.

Now try the following SAT math problem. I will post a solution after Thanksgiving, but feel free to post your own solutions in the comments meanwhile.

Level 4 SAT Exponential Growth 

On January 1, 2015, a family living on an island releases their two pet rabbits into the wild. Due to the short gestation period of rabbits, and the fact that the rabbits have no natural predators on this island, the rabbit population doubles each month. If P represents the rabbit population  years after January 1, 2015, then which of the following equations best models the rabbit population on this island over time?

A) P = 2^{t/12 + 1}
B) P = 2^{t + 1}
C) P = 2^12t
D) P = 2^{12t + 1}

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Hard SAT and ACT Math Problem with Solution

Quadratic Equations

Today I would like to provide a solution to yesterday’s hard math problem involving quadratic equations. Here is the problem once again, followed by a solution.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x² – 70x + 25 = 0
B. 49x² + 70x + 25 = 0
C. 49x² + 35x + 25 = 0
D. 49x² + 25 = 0
E. 49x² – 25 = 0

* If -5/7  is the only solution, then x + 5/7  is the only factor (by the factor theorem). So we have

(x + 5/7)(x + 5/7) = 0

x² + 5/7 x + 5/7 x + (5/7)² = 0

x² + 10/7 x + 25/49 = 0

49x² + 70x + 25 = 0

This is choice B.

Notes: (1) The factor theorem says that r is a root of the polynomial p(x) if and only if x – r is a factor of the polynomial.

(2) In factored form, a quadratic equation always has two factors. Since x + 5/7 is the only factor in this problem, it must appear twice.

(3) In going from the first equation to the second equation, we multiplied the two polynomials (x + 5/7  times itself). To do this you can use FOIL or any other method you like for multiplying polynomials.

(4) In going from the second equation to the third equation, we simply added  5/7 x + 5/7 x = 10/7 x.

(5) In going from the third equation to the last equation, we multiplied both sides of the equation by the least common denominator, which is 49. More precisely, on the left hand side we have

49(x² +10/7 x + 25/49)

= 49x² + 49(10/7 x) + 49(25/49)

= 49x² +7(10x) + 25

= 49x² +70x + 25.

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends: