500 New SAT Math Problems
Just 19.99 on Amazon
Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.
The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.
The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems
If you have any questions, feel free to contact me at steve@SATPrepGet800.com
Thank you all for your continued support!
A Trick For Free Two Day Shipping
I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.
Sign Up For Amazon Prime For Free
If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.
This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.
After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.
Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.
Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:
Sign Up For Amazon Prime For Free
If you think your friends might be interested in this special offer, please share it with them on Facebook:
Thank you all for your continued support!
 |
 |
 |
 |
 |
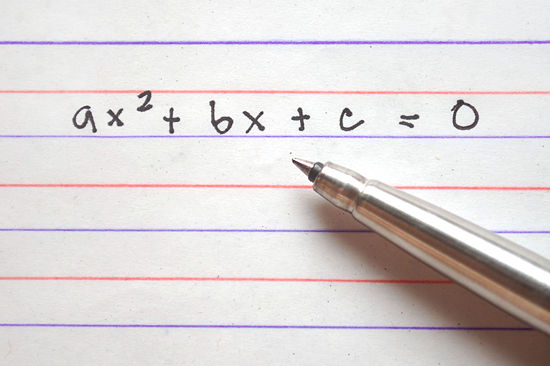
Hard SAT and ACT Math Problem
Quadratic Equations
Today I would like to give a hard math problem involving quadratic equations. This question type can show up on both the SAT and ACT. I will provide a full explanation for this problem soon. Feel free to leave your own solutions in the comments.
Level 5 Quadratic Equations
Which of the following is a quadratic equation that has –5/7 as its only solution?
A. 49x2 – 70x + 25 = 0
B. 49x2 + 70x + 25 = 0
C. 49x2 + 35x + 25 = 0
D. 49x2 + 25 = 0
E. 49x2 – 25 = 0
More SAT and ACT Math Problems with Explanations
If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
Hard SAT and ACT Math Problem with Solution
System of Inequalities
Today I would like to provide a solution to yesterday’s SAT/ACT problem involving a system of inequalities. Here is the problem once again, followed by a solution.
Level 5 System of Inequalities
y ≤ 2x + 2
y ≥ –3x – 3
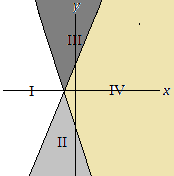
A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?
A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV
Solution: The line y = 2x + 2 has a slope of 2 > 0, and therefore the graph is the line that moves upwards as it is drawn from left to right.
The point (0,0) satisfies the inequality y ≤ 2x + 2 since 0 ≤ 2(0) + 2, or equivalently 0 ≤ 2 is true.
It follows that the graph of y ≤ 2x + 2 consists of sections II and IV.
The line y = –3x – 3 has a slope of –3 < 0, and therefore the graph is a line that moves downwards as it is drawn from left to right.
(0,0) satisfies the inequality y ≥ –3x – 3 since 0 ≥ –3(0) – 3, or equivalently 0 ≥ –3 is true.
It follows that the graph of y ≥ –3x – 3 consists of sections III and IV.
The intersection of the two solution graphs is section IV, choice B.
Note: For a more detailed explanation, see 28 New SAT Math Lessons – Advanced Course
More SAT and ACT Math Problems with Explanations
If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
Hard SAT and ACT Math Problem
System of Inequalities
Today I would like to give a hard math problem involving a system of inequalities. This type of question can show up on both the SAT and ACT. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.
Level 5 System of Inequalities
y ≤ 2x + 2
y ≥ –3x – 3
A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?
A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV
More SAT and ACT Math Problems with Explanations
If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
More On The Triangle Rule
Yesterday we discussed the triangle rule, and I provided a few problems from standardized tests where the triangle rule was extremely useful. and it was not hard to see how this simple rule should be applied.
Recall that the triangle rule states that that the length of the third side of a triangle is between the sum and difference of the lengths of the other two sides.
This can be written symbolically as “difference < x < sum” where x is the third side of the triangle.
Today let us look at another type of problem that the triangle rule should be used to solve.
Problems involving distances between three points can often be solved using the triangle rule. After all, when you plot three points and look at the distances between each pair of points, you are looking at the lengths of the sides of a triangle.
Try plotting three points on a piece of paper and you you will immediately see what I mean.
There is a small catch however – sometimes when you plot three points, the points can be collinear: that is they all lie on the same line.
This means that the symbol “<” in the triangle rule should be replaced by the symbol “≤.”
In other words, this time we write “difference ≤ x ≤ sum.”
Let’s look at an example that could appear on a standardized math test.
Points Q, R and S lie in a plane. If the distance between Q and R is 18 and the distance between R and S is 11, which of the following could be the distance between Q and S?
II. 28
III. 29
A) I only
B) II only
C) III only
D) I and III
E) I, II and III
Solution: Okay, to solve this problem, of course we are going to use the triangle rule… In this case, if Q, R and S form a triangle, then the length of QS is between 18 – 11 = 7 and also 18 + 11 = 29. The extreme cases 7 and 29 form straight lines. In this problem that is fine, so the distance between Q and S is between 7 and 29, inclusive. Thus, the answer is choice (E).
You can see how quickly this problem can be solved when the triangle rule is used.
If you want more practice, then please check out the Get 800 collection of test prep books. These have more examples of problems that need to use this rule for efficient and correct answering.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
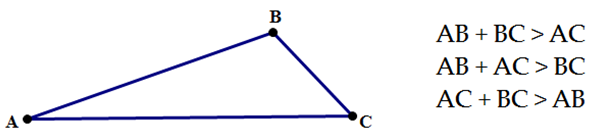
The Triangle Rule
I consider using the triangle rule to be an advanced math strategy for standardized tests. It generally comes up on level 4 and 5 problems on the SAT, ACT and GRE, and the only reason so many students get these problems wrong is because they have never been taught the rule in school.
The triangle rule states that that the length of the third side of a triangle is between the sum and difference of the lengths of the other two sides.
So, for example, if we knew that a triangle had two sides of lengths 5 and 7, respectively, then we could find the possible lengths of the third side by using the triangle rule. Simply note that the sum is
7 + 5 = 12
and the difference is
7 – 5 = 2.
Therefore, the the length of third side lies between 2 and 12.
Let’s get our heads around this with another short example:
Example 1
If a triangle has sides of lengths 2, 5, and x, then we have that
5 – 2 < x < 5 + 2.
That is,
3 < x < 7.
The triangle rule is a very easy concept to understand. Again, the only reason why these are considered tough problems is because the rule is not emphasized in school, and sometimes not taught at all.
So let’s really get this rule into practice by solving some problems that might actually appear on a standardized test.
Example 2
The lengths of the sides of a triangle are x, 8, and 15, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?
Solution: The triangle rule tells us that
15 – 8 < x < 15 + 8.
That is,
7 < x < 23.
Since x is the shortest side, x < 8. So we must choose a number between 7 and 8. If this were a grid in problem (such as on the SAT or GRE), we could grid in 7.1 or any other decimal or improper fraction between 7 and 8. But inputting 7 or 8 as the answer would be incorrect as these integers are not between 7 and 8!
Okay, one more. This one is a multiple choice question.
Example 3
If x is an integer greater than 5, how many different triangles are there with sides of length 3, 5 and x?
A) One
B) Two
C) Three
D) Four
E) Five
Solution: The triangle rule tells us that
5 – 3 < x < 5 + 3.
That is,
2 < x < 8.
Since x is an integer greater than 5, x can be 6 or 7. So there are two possibilities, choice B.
My students find these problems very straight forward. I hope you do too. But it can be easy to forget the rule you need to use if you do not practice enough with it. If you want more practice, then please check out the Get 800 collection of test prep books. These have more examples of problems that need to use this rule for efficient and correct answering.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
Hard ACT Math Probability Problem with Solution
Today I will give a solution to yesterday’s ACT math probability problem. Here is the question again followed by a ful solution.
Level 5 Probability
Suppose that x will be randomly selected from the set
{–3/2, –1, –1/2, 0, 5/2}
and that y will be randomly selected from the set
{–3/4, –1/4, 2, 11/4}.
What is the probability that x/y < 0 ?
A. 1/100
B. 1/20
C. 3/20
D. 1/3
E. 2/5
Solution: There are 5 possible values for x and 4 possible values for y. By the counting principle, there are 5 ⋅ 4 = 20 possibilities for xy (possibly with some repetition).
In order for x/y < 0 to be true, x and y need to be opposite in sign. The number of ways for this to happen (possibly with repetition) is
3 ⋅ 2 + 1 ⋅ 2 = 6 + 2 = 8
So the desired probability is 8/20 = 2/5, choice E.
Notes: (1) In this question when we mention the possibilities for xy, we are ignoring the fact that there could be repeated values. For example, we have (0)(–3/4) = 0 and (0)(–1/4) = 0. Technically these two computations give a single value for xy. Nonetheless, to compute the desired probability we need to think of these as distinct possibilities.
(2) There are 3 negative values for x and 2 positive values for y. This gives us 3 ⋅ 2 = 6 negative values for xy.
There is 1 positive value for x and 2 negative values for y. This gives us 1 ⋅ 2 = 2 more negative values for xy.
So altogether there are 6 + 2 = 8 possibilities that lead to a negative value for xy.
More ACT Math Problems with Explanations
If you are preparing for the ACT, you may want to take a look at the following book.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
Hard ACT Math Probability Problem
Today I would like to give a hard ACT math probability problem. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.
Level 5 Probability
Suppose that x will be randomly selected from the set
{–3/2, –1, –1/2, 0, 5/2}
and that y will be randomly selected from the set
{–3/4, –1/4, 2, 11/4}.
What is the probability that x/y < 0 ?
A. 1/100
B. 1/20
C. 3/20
D. 1/3
E. 2/5
More ACT Math Problems with Explanations
If you are preparing for the ACT, you may want to take a look at the following book.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
ACT Math Number Theory Problem with Solutions
Today I will give a solution to yesterday’s ACT math number theory problem. Here is the question one more time followed by a full solution.
Level 3 Number Theory
What positive number when divided by its reciprocal has a result of 9/16?
A. 8/3
B. 3/8
C. 4/3
D. 3/16
E. 3/4
Solution by starting with choice C: Let’s start with 4/3 as our first guess. The reciprocal of 4/3 is 3/4, and when we divide 4/3 by 3/4, we get 16/9. This is not correct, but it is the reciprocal of what we are trying to get. So the answer is the reciprocal of 4/3, which is 3/4, choice E.
Notes: (1) The reciprocal of the fraction a/b is the fraction b/a. In other words, we get the reciprocal of the fraction by interchanging the number on top (the numerator) with the number on bottom (the denominator).
(2) We can divide 4/3 by 3/4 right in our TI-84 calculator by typing
(4 / 3) / (3 / 4) ENTER MATH ENTER ENTER
The output will be 16/9.
Pressing MATH ENTER ENTER at the end changes the decimal to a fraction.
(3) We can also do the computation by hand as follows:
(4) Let’s also just confirm that choice E is the answer. I’ll use the hand method, but you can also feel free to use your calculator.
* Algebraic solution: Let x be the positive number. We are given that
Since we are given that x is a positive number, x = 3/4, choice E.
More ACT Math Problems with Explanations
If you are preparing for the ACT, you may want to take a look at the following book.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
ACT Math Number Theory Problem
Today I would like to give an ACT math number theory problem. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.
Level 3 Number Theory
What positive number when divided by its reciprocal has a result of 9/16?
A. 8/3
B. 3/8
C. 4/3
D. 3/16
E. 3/4
More ACT Math Problems with Explanations
If you are preparing for the ACT, you may want to take a look at the following book.
And if you liked this article, please share it with your Facebook friends:
|
|
|
|
|
Distance Rate Time Charts
Yesterday we discussed how to solve a certain type of rate problem very quickly simply by plugging numbers into a simple formula. In case you are interested you can find that post here: Xiggi’s formula.
In yesterday’s post we learned that Xiggi’s formula can be used to find an average rate when two individual rates for the same distance are known.
But what if we want to find the distance or time instead?
If the two distances are the same, then Xiggi’s formula can still be used but the solution will require a little more work. In this case however Xiggi’s formula is probably not the most efficient way to solve the problem.
Also, what if we want to solve a rate problem where the two (or more) distances are different?
Well in this case we certainly cannot use Xiggi’s formula. Another method will be needed.
In this blog post I would like to go over a method of solution that will work for any math problem involving distances, rates and times that show up on standardized tests such as the SAT, ACT and GRE. Today we will carefully go over how to set up a “distance = rate · time” chart.
Let’s start right away with an example.
Marco drove from home to work at an average speed of 50 miles per hour and returned home along the same route at an average speed of 46 miles per hour. If his total driving time for the trip was 4 hours, how many minutes did it take Marco to drive from work to home?
Let’s solve this problem by writing out a “distance = rate · time” chart.
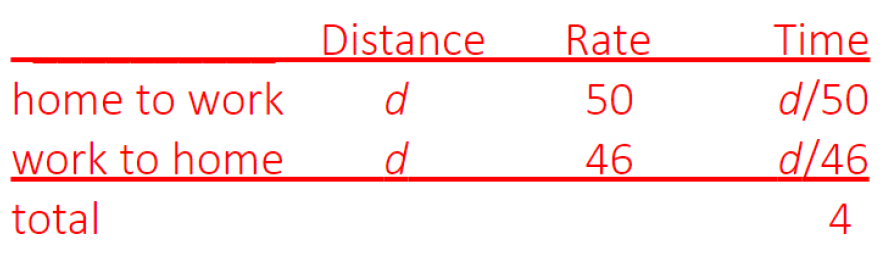
Note that although we do not know either distance, we do know that they are the same, so we can call them both “d.” Also, since
distance = rate · time,
we have that
We use this to get the first two entries in column three. The total time is given in the question. So we have
46d + 50d = 4 · 50 · 46
96d = 4 · 50 · 46
We want the time it takes Marco to drive from work to home, that is we want to compute d/46.
In hours, this is equal to
To convert to minutes we multiply by 60.
Let’s also try to solve this problem using Xiggi’s formula.
We have
Finally to convert from hours to minutes we multiply by 60 and get 125.
Notice that this particular problem was not so straightforward to solve using Xiggi’s formula. Compare this to the problem in yesterday’s blog post. Do you see the difference? In last week’s question we were being asked to find a rate, whereas in this question we were asked to find a time.
Toward the end of yesterday’s post you were asked to solve the following problem:
Jason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?
Let’s first solve this problem using Xiggi’s formula.
So we can grid in 8.55 or 8.56.
And now here is a solution using a “distance = rate · time” chart.
So we grid in 8.55 or 8.56.
More Hard Practice Problems
For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.
If you liked this article, please share it with your Facebook friends:
Speak to you soon!
|
|
|
|
|