AP Calculus Archives

500 New SAT Math Problems – Just 19.99 Today Only

June 30, 2024

$500 New SAT Math Problems$

500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

~~The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.~~

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

AP Calculus Crash Course and Information

May 2, 2020

AP Calculus Crash Course and Information

The upcoming AP exams will be unusual due to the Covid-19 outbreak. This year the exams will essentially be take home tests. The information I present here is specifically for the AP Calculus exams. You can find information on all the AP exams at the College Board’s website here: AP Exam Information

I’d like to begin with a short list of the most important things you should know about the AP Calculus exams this year:

Both AP Calculus exams will be administered on Tuesday, May 12, 2020 at 2 PM Eastern Standard Time.
Each test will consist of just two free-response questions.
You will have 30 minutes to complete and upload the first question (25 minutes to write your solution and another 5 minutes to upload your solution). This question will account for 60% of your grade.
You will have 20 minutes to complete and upload the second question (15 minutes to write your solution and another 5 minutes to upload your solution). This question will account for 40% of your grade.
Each question will require you to understand topics from at least two units.
A calculator is not required for either question. However, you may use a calculator if you wish.
Some topics that usually appear on the AP Calculus exams will be excluded. In particular, for the AB exam, you will not be tested on applications of integration. For example, you will not need to be able to compute any of the following: the area between two curves, cross sectional volumes, volumes of solids of revolution, average value over an interval, and other applications of integration.

To help students prepare for the exam this year, I will be running an AP Calculus AB crash course via live video (Zoom). Beginning Sunday, May 3 at 4:30 PM, I will be spending 15 to 20 minutes going over AP Calculus AB problems. The classes will be interactive. I will answer questions and provide clarifications in real time. I will then spend additional time after completing the problems to answer any further questions. If you would like to sign up for all the classes, use the following link to register:

AP Calculus AB Crash Course

If you would like to register for individual sessions or you would like more information, you can email me at:

support@SATPrepGet800.com

If you think that people you know might be interested in this crash course for themselves or their children, please share it with them on Facebook:

Thank you all for your continued support!

AP Calculus Intensives

April 4, 2020

AP Calculus Information and Intensives

I’d like to begin with a short list of the most important things you should know about the AP Calculus exams this year:

Both AP Calculus exams will be administered on Tuesday, May 12, 2020 at 2 PM Eastern Standard Time.
Each test will consist of just two free-response questions.
You will have 30 minutes to complete and upload the first question (25 minutes to write your solution and another 5 minutes to upload your solution). This question will account for 60% of your grade.
You will have 20 minutes to complete and upload the second question (15 minutes to write your solution and another 5 minutes to upload your solution). This question will account for 40% of your grade.
Each question will require you to understand topics from at least two units.
A calculator is not required for either question. However, you may use a calculator if you wish.
Some topics that usually appear on the AP Calculus exams will be excluded. In particular, for the AB exam, you will not be tested on applications of integration. For example, you will not need to be able to compute any of the following: the area between two curves, cross sectional volumes, volumes of solids of revolution, average value over an interval, and other applications of integration.

To help students prepare for the exam this year, I will be running four 30- minute AP Calculus AB intensive sessions via live video (Zoom) at a price of $10 per session. The topics I have chosen are based upon what I have found that students have the most difficulty with and what I think is likely to appear on the AB exam. Here is the list of topics:

Position, Velocity, and Acceleration
Intermediate and Mean Value Theorems
Related Rates
Differential Equations

If you would like to be notified of these AP Calculus AB Intensive classes, please click the following link and enter your email address:

AP Calculus AB Intensives – Notification List

If you think that people you know might be interested in these intensive sessions for themselves or their children, please share it with them on Facebook:

Thank you all for your continued support!

320 AP Calculus BC Problems – Half Price

January 27, 2017

320 AP Calculus BC Problems – Half Price!

I just want to let everyone know that Amazon currently has the second edition of 320 AP Calculus BC Problems on sale for 50% off. There is no way for me to know how long Amazon will leave the book on sale. Here is a link to the book’s Amazon page: 320 AP Calculus BC Problems

If you are studying for the BC exam or teaching a review course, make sure that you have the latest edition of the book. For information on the changes being implemented for the 2017 AP Calculus BC exam, follow this link: AP Calculus BC Exam Changes Beginning 2016-2017

My New AP Calculus Social Media Accounts

Don’t forget to like my new AP Calculus Facebook page, and follow my new AP Calculus Twitter account.

If you think your friends might be interested in this sale, please share it with them on Facebook:

Thank you all for your continued support!

AP Calculus BC Problem with Solution – Arc Length

August 10, 2016

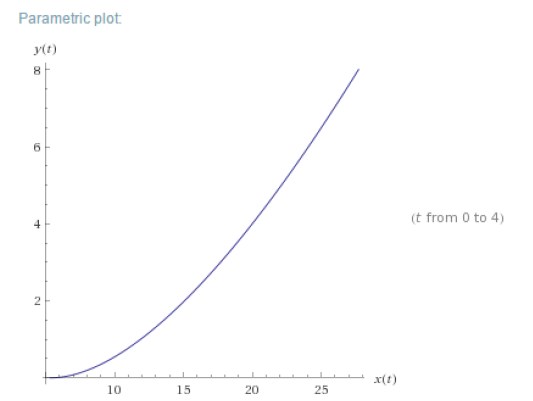
AP Calculus BC Problem with Solution – Arc Length

Today I will give a solution to the AP Calculus BC Arc Length problem I gave yesterday.

Level 2 Arc Length

Find the length of the arc of the curve defined by

$x(t)=\frac{1}{12}(8t+16)^{\frac{3}{2}}, \quad y(t)=\frac{t^2}{2}$

from t = 0 to t = 4.

Solution:

$\frac{dx}{dt}=(\frac{1}{12})(\frac{3}{2})(8t+16)^{\frac{1}{2}}(8)=\sqrt{8t+16}$

and

$\frac{dy}{dt}=t$

So,

$(\frac{dx}{dt})^2=8t+16$

and

$(\frac{dy}{dt})^2=t^2$

So the desired length is

$\int_0^4 \sqrt{8t+16+t^2} \ dt$

$=\int_0^4 \sqrt{t^2+8t+16} \ dt$

$=\int_0^4 \sqrt{(t+4)^2} \ dt$

$=\int_0^4 (t+4) \ dt$

$=(\frac{t^2}{2}+4t)|_0^4$

$=(\frac{4^2}{2}+4\cdot 4)$

$=8+16$

$=\bf{24}$

Notes: (1) The arc length of the differentiable curve with parametric equations x = x(t) and y = y(t) from a to b is

$\text{Arc Length}=\int_a^b \sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2} \ dt$

(2) We used the chain rule to compute dx/dt and a simple power rule to compute dy/dt. See problem 2 in 320 AP Calculus BC Problems for more information on the chain rule.

AP Calculus BC Problem- Arc Length

Today I would like to give an AP Calculus BC problem involving arc length. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 2 Arc Length

Find the length of the arc of the curve defined by

x(t) = 1/12 (8t + 16)^3/2 and y(t) = t²/2,

from t = 0 to t = 4.

The Fence-Post Formula

Today I want to discuss a math concept that can be used to solve certain types of problems that appear every now and then on standardized tests. Tutors tend not to spend much time (if any) helping students prepare for this type of problem as it seldom appears. But if you want a perfect math score, then you want to be able to recognize all problem types and be able to answer them correctly (and quickly!).

This problem type involves what I like to call “Fence-Posting,” a technique that allows us to count the number of integers in a consecutive list.

Fence-post formula: The number of integers from a to b, inclusive, is

b – a + 1.

The word inclusive means that we include the extreme values.

For example, if we want to count the integers from 1 to 3, inclusive, we can easily see that there are 3 of them. Note that we do include the extreme values 1 and 3. Using the fence-post formula we get

3 – 1 + 1 = 3.

The most common error when attempting to count the integers in a list is to simply subtract the smallest value from the largest value (without adding 1). Note that in the previous example, this would give an incorrect answer of 2.

As another simple example, let’s count the number of integers from 5 to 12, inclusive, in two ways – directly and by fence-posting. First directly – the integers from 5 to 12 are 5, 6, 7, 8, 9, 10, 11, 12, and we see that there are 8 of them. Now using the fence-post formula we have

12 – 5 + 1 = 8.

Note that the computation 12 – 5 gives an incorrect answer of 7.

If you ever happen to forget this little formula test it out on a small list of numbers as I just did in the two examples above. But it’s nice to have this one committed to memory so that it is there for you when you need it.

Let’s take a look at a couple of examples where we can use fence-posting to obtain an answer efficiently.

Example 1

Set X contains only the integers 0 through 180 inclusive. If a number is selected at random from X, what is the probability that the number selected will be greater than the median of the numbers in X?

So first of all we need to find out how many integers there are in the set X. By the fence-post formula there are

180 – 0 + 1 = 181

integers in this set.

The median of the numbers in set X is 90 (note that in a set of consecutive integers the median is equal to the average of the first and last integer). Again, by the fence-post formula, we see that there are

180 – 91 + 1 = 90

integers greater than the median.

From this we see that the desired probability is

90/181 (approximately 0.4972375691).

So we grid in .497. (Note that this is a grid-in question because I have not provided answer choices).

Remember with grid in problems, we have only four slots available. We can simply truncate the final answer that we get in our calculator to fit in the four slots.

Example 2

How many numbers between 72 and 356 can be expressed as 5x + 3, where x is an integer?

This problem is more complicated than the first example, but we can use fence-posting to solve this one too: Let’s start by guessing x-values until we find the smallest and largest values of x satisfying

72 < 5x + 3 < 356.

Since we have 5(13) + 3 = 68 and also 5(14) + 3 = 73 we see that 14 is the smallest value of x satisfying the inequality.

Since 5(70) + 3 = 353 and 5(71) + 3 = 358, the largest value of x satisfying the inequality is 70.

It follows by fence-posting that the answer is 70 – 14 + 1 = 57.

Note that we also used the strategy of taking a guess to solve this problem. I discussed this strategy in a previous blog post. You can find that information by clicking on the link.

Algebraic solution:

72 < 5x + 3 < 356
69 < 5x < 353
69/5 < x < 353/5
13.8 < x < 70.6
14 ≤ x ≤ 70

We get the last inequality because x must be an integer. Notice that this last inequality is not strict. For those of you not familiar with this piece of math lingo, an inequality that is not strict means that it is ‘less than or equal to’ rather than just ‘less than’.

Finally, t follows by fence-posting that the answer is 70 – 14 + 1 = 57.

Tomorrow I will be showing a quick method for computing differences of large sums. You will also see how the fence-post formula can sometimes be useful in solving these types of problems. Click the following link to read this article: Differences of Large Sums

AP Calculus AB Mean Value Theorem

Problem with Solution

Today I will provide a solution for yesterday’s AP Calculus AB Mean Value Theorem Problem. Once again here is the question:

Let f(x) = –3x²+ x – 5. A value of c that satisfies the conclusion of the Mean Value Theorem for f on the interval [–2,2] is

(A) –2
(B) –1/2
(C) –1/6
(D) 0

Solution: f ‘ (x)= –6x + 1, so that f ‘ (c) = –6c + 1.

f(2) = -3(2)²+ 2 – 5 = –3(4) – 3 = –12 – 3 = –15.

f(–2) = –3(–2)²– 2 – 5 = –3(4) – 7 = –12 – 7 = –19.

We now solve the equation f ‘ (c) = (f(2) – f(–2)) / (2 – (–2)) to get

–6c + 1 = (–15 – (–19)) / (2 + 2) = (–15 + 19) / 4 = 4 / 4 = 1

So –6c = 1 – 1 = 0, and c=0, choice (D).

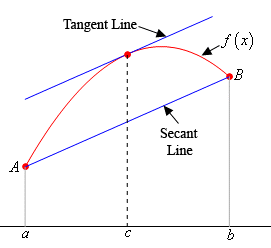
Notes: (1) The Mean Value Theorem says that if f is a function that is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there is a real number c with a < c < b such that f ‘ (c) = (f(b) – f(a)) / (b – a).

In this problem a = –2, b = 2, and f(x) = –3x² + x – 5.

(2) Note that the function f(x) = –3x² + x – 5 is a polynomial. It is therefore continuous and differentiable everywhere. In particular, it is continuous on [–2,2] and differentiable on (–2,2). Therefore by the Mean Value Theorem, there is a c between –2 and 2 such that

f ‘ (c) = (f(2) – f(–2)) / (2 – (–2)).

(3) Geometrically, f ‘ (c) is the slope of the tangent line to the graph of the function f at c, and (f(b) – f(a)) / (b – a) is the slope of the secant line passing through the points A(a,f(a)), and B(b,f(b)).

The Mean Value Theorem says that the slopes of these two lines are the same. In other words, they are parallel.

AP Calculus AB – Mean Value Theorem

AP Calculus students tend to find problems involving the Mean Value Theorem very difficult. I often tell my students “If you don’t know what a problem is asking for, try using the Mean Value Theorem.” This is due to the fact that most problems where the Mean Value Theorem is needed never actually mention the theorem in the problem itself.

Let’s try a very basic AP Calculus AB Mean Value Theorem problem (note that any Calculus AB problem can also appear on the BC exam). I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 2 Mean Value Theorem Problem

Let f(x) = –3x²+ x – 5. A value of c that satisfies the conclusion of the Mean Value Theorem for f on the interval [–2,2] is

(A) –2
(B) –1/2
(C) –1/6
(D) 0

AP Calculus BC Geometric Series Problem

With Solution

Yesterday I gave an AP Calculus BC problems involving a geometric series. You can find that post here: AP Calculus BC Problem – Geometric Series.

Today I will provide a solution to that problem. First, here is the question one more time.

Level 2 Series

$g(x)=\Sigma_{n=1}^{\infty}(sin^2 x)^n$

If g is the function given above, then g(π/3) =

(A) 3
(B) 1
(C) 3/4
(D) 1/2

Solution:
$g(\frac{\pi}{3})$
$=\Sigma_{n=1}^{\infty}(sin^2(\frac{\pi}{3}))^n$
$=\Sigma_{n=1}^{\infty}((\frac{\sqrt{3}}{2})^2)^n$
$=\Sigma_{n=1}^{\infty}(\frac{3}{4})^n$
$=\frac{\frac{3}{4}}{1-\frac{3}{4}}$
$=\frac{3}{4}\div \frac{1}{4}$
$=\frac{3}{4}\cdot 4$
$=3$
Note:
$\Sigma_{n=1}^{\infty}(\frac{3}{4})^n$

is an infinite geometric series with first term a = 3/4 and common ratio r = 3/4. Watch the video above for more information on geometric series.

AP Calculus BC Problem- Geometric Series

AP Calculus BC problems involving series tend to be difficult for students. I thought I would start things off easy today with a level 2 problem involving geometric series. Those of you that have forgotten the basics of geometric series should find the video above helpful.

Let’s now try an AP Calculus BC series problem. AB students do not need to worry about this one. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 2 Series

$g(x)=\Sigma_{n=1}^{\infty}(sin^2 x)^n$

If g is the function given above, then g(π/3) =

(A) 3
(B) 1
(C) 3/4
(D) 1/2

$500 New SAT Math Problems$