SAT Math Subject Tests Archives

500 New SAT Math Problems – Just 19.99 Today Only

June 30, 2024

$500 New SAT Math Problems$

500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

~~The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.~~

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Complex Numbers

August 10, 2017

Hard Statistics Problem with Solution

January 4, 2017

$320 SAT Math Subject Test Problems - Level 2$

Hard Statistics Problem with Solution

Today I would like to give a solution to yesterday’s statistics problem. Before reading the solution, you may want to review the following article: Changing Averages to Sums

Here is the problem once again, followed by a solution.

Level 5 Statistics

Suppose that the average (arithmetic mean) of a, b, and c is h, the average of b, c, and d is j, the average of c, d, and e is k, and the average of d, e, and f is m. What is the value of (a + c) – (d + f ) ?

A) h – j + k – m
B) 3(h – j + k – m)
C) 3/4 (h – j + k – m)
D) 3(h + j + k + m)
E) 3/4 (h + j + k + m)

Solution by changing averages to sums: We have

a + b + c = 3h

b + c + d = 3j

c + d + e = 3k

d + e + f = 3m

We subtract the second equation from the first equation to get

a – d = 3h – 3j

We subtract the fourth equation from the third equation to get

c – f = 3k – 3m

We now add these last two equations to get

a – d + c – f = 3h – 3j + 3k – 3m

This is equivalent to choice B.

Hard Statistics Problem

Today I would like to give a hard statistics problem from the book 320 SAT Math Subject Test Problems – Level 2. I will provide a full explanation for this problem tomorrow. Feel free to leave your own solutions in the comments.

Level 5 Statistics

A) h – j + k – m
B) 3(h – j + k – m)
C) 3/4 (h – j + k – m)
D) 3(h + j + k + m)
E) 3/4 (h + j + k + m)

SAT Exponential Growth Problem with Solution

Today I would like to give a solution to the SAT exponential growth problem presented in this post: Exponential Growth and Decay

Here is the problem once again, followed by a solution.

Level 4 SAT Exponential Growth

On January 1, 2015, a family living on an island releases their two pet rabbits into the wild. Due to the short gestation period of rabbits, and the fact that the rabbits have no natural predators on this island, the rabbit population doubles each month. If P represents the rabbit population years after January 1, 2015, then which of the following equations best models the rabbit population on this island over time?

A) P = 2^{t/12 + 1}
B) P = 2^{t + 1}
C) P = 2^12t
D) P = 2^{12t + 1}

Solution using the exponential growth model formula: As seen in example (4) from this post, a quantity that continually doubles over a fixed time period can be modeled by the exponential function P = a(2)^t/d where a is the quantity at time t = 0, and d is the doubling time in years. In this case, there are initially 2 rabbits, so that a = 2, and the doubling time is every month, or every 1/12 year.

It follows that P = 2(2)^{t ÷ 1/12}= 2(2)^12t= 2¹2^12t= 2^{1 + 12t}= 2^{12t + 1}, choice (D).

Notes: (1) For a review of the laws of exponents used here, see the following post: Laws of Exponents

(2) For additional methods for solving this problem, you may want to take a look at 28 New SAT Math Lessons – Advanced Course

Exponential Growth and Decay

The current version of the SAT gives problems on exponential growth and decay. Here are the basics that you should know if you want to get a perfect SAT score:

A general exponential function has the form f(t) = a(1 + r)^ct, where a = f(0) is the initial amount and r is the growth rate. If r > 0, then we have exponential growth and if r < 0 we have exponential decay.

Examples: (1) The exponential function f(t) = 300(2)^t can be used to model a population with a growth rate of 1 = 100% each year that begins with 300 specimens. The growth rate of 100% tells us that the population doubles each year.

(2) The exponential function f(t) = 50(3)^2t can be used to model a population with a growth rate of 2 = 200% every 6 months that begins with 50 specimens. The growth rate of 200% tells us that the population triples. Since c = 2, the tripling occurs every 1/2 year or 6 months.

(3) The exponential function f(t) = 120(0.75)^t/3 can be used to model a substance which is decaying at a rate of 1 – 0.75 = 0.25 = 25% every 3 years. The initial amount of the substance might be 120 grams. Since c = 1/3, the 25% decay occurs every 3 years.

(4) A quantity that continually doubles over a fixed time period can be modeled by the exponential function f(t) = a(2)^t/d where a is the quantity at time t = 0, and d is the doubling time in years.

Now try the following SAT math problem. I will post a solution after Thanksgiving, but feel free to post your own solutions in the comments meanwhile.

Level 4 SAT Exponential Growth

A) P = 2^{t/12 + 1}
B) P = 2^{t + 1}
C) P = 2^12t
D) P = 2^{12t + 1}

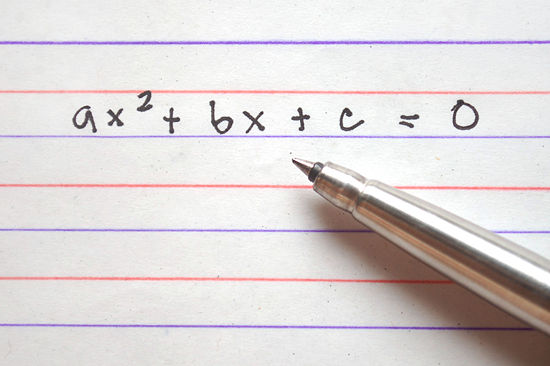
Hard SAT and ACT Math Problem with Solution

Quadratic Equations

Today I would like to provide a solution to yesterday’s hard math problem involving quadratic equations. Here is the problem once again, followed by a solution.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x²– 70x + 25 = 0
B. 49x²+ 70x + 25 = 0
C. 49x²+ 35x + 25 = 0
D. 49x²+ 25 = 0
E. 49x²– 25 = 0

* If -5/7 is the only solution, then x + 5/7 is the only factor (by the factor theorem). So we have

(x + 5/7)(x + 5/7) = 0

x² + 5/7 x + 5/7 x + (5/7)² = 0

x² + 10/7 x + 25/49 = 0

49x² + 70x + 25 = 0

This is choice B.

Notes: (1) The factor theorem says that r is a root of the polynomial p(x) if and only if x – r is a factor of the polynomial.

(2) In factored form, a quadratic equation always has two factors. Since x + 5/7 is the only factor in this problem, it must appear twice.

(3) In going from the first equation to the second equation, we multiplied the two polynomials (x + 5/7 times itself). To do this you can use FOIL or any other method you like for multiplying polynomials.

(4) In going from the second equation to the third equation, we simply added 5/7 x + 5/7 x = 10/7 x.

(5) In going from the third equation to the last equation, we multiplied both sides of the equation by the least common denominator, which is 49. More precisely, on the left hand side we have

49(x² +10/7 x + 25/49)

= 49x² + 49(10/7 x) + 49(25/49)

= 49x² +7(10x) + 25

= 49x² +70x + 25.

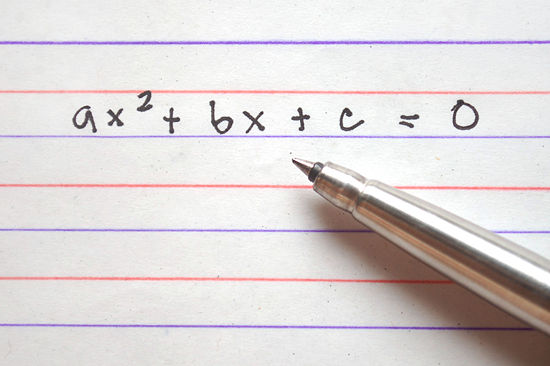
Hard SAT and ACT Math Problem

Quadratic Equations

Today I would like to give a hard math problem involving quadratic equations. This question type can show up on both the SAT and ACT. I will provide a full explanation for this problem soon. Feel free to leave your own solutions in the comments.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x²– 70x + 25 = 0
B. 49x²+ 70x + 25 = 0
C. 49x²+ 35x + 25 = 0
D. 49x²+ 25 = 0
E. 49x²– 25 = 0

Hard SAT and ACT Math Problem with Solution

System of Inequalities

Today I would like to provide a solution to yesterday’s SAT/ACT problem involving a system of inequalities. Here is the problem once again, followed by a solution.

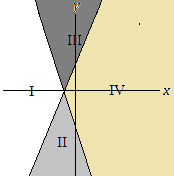
Level 5 System of Inequalities

y ≤ 2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

Solution: The line y = 2x + 2 has a slope of 2 > 0, and therefore the graph is the line that moves upwards as it is drawn from left to right.

The point (0,0) satisfies the inequality y ≤ 2x + 2 since 0 ≤ 2(0) + 2, or equivalently 0 ≤ 2 is true.

It follows that the graph of y ≤ 2x + 2 consists of sections II and IV.

The line y = –3x – 3 has a slope of –3 < 0, and therefore the graph is a line that moves downwards as it is drawn from left to right.

(0,0) satisfies the inequality y ≥ –3x – 3 since 0 ≥ –3(0) – 3, or equivalently 0 ≥ –3 is true.

It follows that the graph of y ≥ –3x – 3 consists of sections III and IV.

The intersection of the two solution graphs is section IV, choice B.

Note: For a more detailed explanation, see 28 New SAT Math Lessons – Advanced Course

Hard SAT and ACT Math Problem

System of Inequalities

Today I would like to give a hard math problem involving a system of inequalities. This type of question can show up on both the SAT and ACT. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 5 System of Inequalities

y ≤ 2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

More On The Triangle Rule

Yesterday we discussed the triangle rule, and I provided a few problems from standardized tests where the triangle rule was extremely useful. and it was not hard to see how this simple rule should be applied.

Recall that the triangle rule states that that the length of the third side of a triangle is between the sum and difference of the lengths of the other two sides.

This can be written symbolically as “difference < x < sum” where x is the third side of the triangle.

Today let us look at another type of problem that the triangle rule should be used to solve.

Problems involving distances between three points can often be solved using the triangle rule. After all, when you plot three points and look at the distances between each pair of points, you are looking at the lengths of the sides of a triangle.

Try plotting three points on a piece of paper and you you will immediately see what I mean.

There is a small catch however – sometimes when you plot three points, the points can be collinear: that is they all lie on the same line.

This means that the symbol “<” in the triangle rule should be replaced by the symbol “≤.”

In other words, this time we write “difference ≤ x ≤ sum.”

Let’s look at an example that could appear on a standardized math test.

Points Q, R and S lie in a plane. If the distance between Q and R is 18 and the distance between R and S is 11, which of the following could be the distance between Q and S?

I. 7
II. 28
III. 29

A) I only
B) II only
C) III only
D) I and III
E) I, II and III

Solution: Okay, to solve this problem, of course we are going to use the triangle rule… In this case, if Q, R and S form a triangle, then the length of QS is between 18 – 11 = 7 and also 18 + 11 = 29. The extreme cases 7 and 29 form straight lines. In this problem that is fine, so the distance between Q and S is between 7 and 29, inclusive. Thus, the answer is choice (E).

You can see how quickly this problem can be solved when the triangle rule is used.

If you want more practice, then please check out the Get 800 collection of test prep books. These have more examples of problems that need to use this rule for efficient and correct answering.

And if you liked this article, please share it with your Facebook friends:

Older posts

$500 New SAT Math Problems$