500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

SAT and SAT Subject Test Dates

The following link will take you to the College Board’s web page showing you the upcoming dates for both the SAT Reasoning Test and the SAT Subject Tests. You can then register right from that page:

Test Dates and Deadlines

If you are an international student, then you should register using the following page instead:

International Registration

And if you are ready to begin preparing for the SAT, you may want to take a look at the Get 800 collection of SAT prep books. Click the follwing picture to see what we offer:
If you think your friends might be interested in this special offer, please share it with them on Facebook:

Distance Rate Time Charts

Yesterday we discussed how to solve a certain type of rate problem very quickly simply by plugging numbers into a simple formula. In case you are interested you can find that post here: Xiggi’s formula.

In yesterday’s post we learned that Xiggi’s formula can be used to find an average rate when two individual rates for the same distance are known.

But what if we want to find the distance or time instead?

If the two distances are the same, then Xiggi’s formula can still be used but the solution will require a little more work. In this case however Xiggi’s formula is probably not the most efficient way to solve the problem.

Also, what if we want to solve a rate problem where the two (or more) distances are different?

Well in this case we certainly cannot use Xiggi’s formula. Another method will be needed.

In this blog post I would like to go over a method of solution that will work for any math problem involving distances, rates and times that show up on standardized tests such as the SAT, ACT and GRE. Today we will carefully go over how to set up a “distance = rate · time” chart.

Let’s start right away with an example.

Marco drove from home to work at an average speed of 50 miles per hour and returned home along the same route at an average speed of 46 miles per hour. If his total driving time for the trip was 4 hours, how many minutes did it take Marco to drive from work to home?

Let’s solve this problem by writing out a “distance = rate · time” chart.

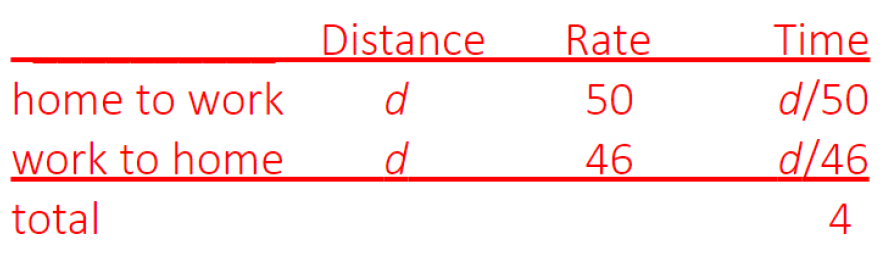
Note that although we do not know either distance, we do know that they are the same, so we can call them both “d.” Also, since

distance = rate · time,

we have that

We use this to get the first two entries in column three. The total time is given in the question. So we have

46d + 50d  = 4 · 50 · 46

96d = 4 · 50 · 46

We want the time it takes Marco to drive from work to home, that is we want to compute d/46.

In hours, this is equal to

To convert to minutes we multiply by 60.

Let’s also try to solve this problem using Xiggi’s formula.

We have

Finally to convert from hours to minutes we multiply by 60 and get 125.

Notice that this particular problem was not so straightforward to solve using Xiggi’s formula. Compare this to the problem in yesterday’s blog post. Do you see the difference? In last week’s question we were being asked to find a rate, whereas in this question we were asked to find a time.

Toward the end of yesterday’s post you were asked to solve the following problem:

Jason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?

Let’s first solve this problem using Xiggi’s formula.

So we can grid in 8.55 or 8.56.

And now here is a solution using a “distance = rate · time” chart.

So we grid in 8.55 or 8.56.

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

Xiggi’s Formula – An Advanced Math Strategy

Hello everyone. This post is mostly for more advanced students that are trying to get an 800 in SAT math (or close to it). That said, the strategy I will be describing here is actually very easy to apply. So even if you are not going for an 800, it will not take too much effort to learn this technique.

Today I would like to talk about Xiggi’s formula.

First of all, some of you may want to know who Xiggi is. Well Xiggi is a frequent poster on the SAT preparation forum of College Confidential.  If you are preparing for the SAT I highly recommend that you utilize this forum as a resource.

The formula I will be discussing in this post is actually called the harmonic mean formula, but on the College Confidential site we all call it Xiggi’s formula. The reason for this is because Xiggi has become well known for helping students on the forum to solve this particular type of problem.

So when should one use Xiggi’s formula? Well, Xiggi’s formula can be used to find an average rate when two individual rates for the same distance are known.

Here is the formula:

Important notes:  (1) Xiggi’s Formula works only when the two distances are the same.

(2) Even though the distance is often given in these types of problems, note that the formula does not use the distance. It uses only the two rates.

(3) For these types of SAT problems, the words “rate” and “speed” are interchangeable.

Here is an example of a problem where Xiggi’s formula is the best way to go:

An elephant traveled 7 miles at an average rate of 4 miles per hour and then traveled the next 7 miles at an average rate of 1 mile per hour. What was the average speed, in miles per hour, of the elephant for the 14 miles?

Let’s solve this problem using Xiggi’s formula. We have

Just to compare, let’s also solve this problem in the more traditional way – by writing out a “distance = rate · time” chart.

Note that we computed the times by using “distance = rate · time” in the form

Finally, we use the formula in the form

Note: To get the total distance we add the two distances, and to get the total time we add the two times. Be careful – this doesn’t work for rates!

SAT, ACT and GRE math problems of this type are always Level 5 problems. But if you know Xiggi’s formula, you can solve this type of question in just a few seconds. So in my opinion, it is well worth committing this one to memory.

Here is another math question where Xiggi’s formula can be useful. Give this one a try on your own.

Jason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?

See if you can solve this problem using Xiggi’s formula. And then also try to solve it with a “distance = rate · time” chart.

I will provide both solutions in tomorrow’s post. But feel free to leave your own solutions in the comments.

Remember that Xiggi’s formula should only be used when the two distances are the same! Should it ALWAYS be used when the distances are the same? We will address this question in next week’s post where we will look at distance, rate, time problems where Xiggi’s formula is not as useful.

Until then, I will leave you with the following “Challenge Problem.”

Use the formula d = rt to derive Xiggi’s formula.

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

Hard GRE Math Arithmetic Problems with Solutions

Yesterday I posted some really hard GRE Arithmetic problems, and today I would like to give you solutions to those problems. Please feel free to post your own solutions or attempted solutions in the comments below as well. If you still want further explanation after reading the below solutions please do not hesitate to ask.

Level 5 GRE Arithmetic Problems with Solutions

1. If n is a positive integer such that the units (ones) digit of n² + 4n is 7 and the units digit of n  is not 7, what is the units digit of n + 3?

Solution: By plugging in values for n, we find that for n = 9,

n² + 4n = 92 + 4 ⋅ 9 = 81 + 36 = 117.

So n = 9 works, and n + 3 = 9 + 3 = 12. So the units digit of n + 3 is 2.

Advanced solution showing the independence of n:

n² + 4n = n(n + 4).

So we are looking at positive integers 4 units apart whose product ends in 7. Since 7 is odd, n must be odd. So n must end in 1, 3, 5, or 9. Note that we skip n = 7 since the problem forbids us from using it.

If n ends in 1, then n + 4 ends in 5, and n(n + 4) ends in 5.
If n ends in 3, then n + 4 ends in 7, and n(n + 4) ends in 1.
If n ends in 5, then n + 4 ends in 9, and n(n + 4) ends in 5.
If n ends in 9, then n + 4 ends in 13, and n(n + 4) ends in 7.

So n ends in a 9, and n + 3 ends in a 2.

2. The sum of the positive odd integers less than 200 is subtracted from the sum of the positive even integers less than or equal to 200. What is the resulting difference?

We write out each sum formally, line them up, and subtract term by term.

2 + 4 + 6 + … + 200
1 + 3 + 5 + … + 199
1 + 1 + 1 + … + 1

Now notice that we’re adding 1 to itself 100 times. So the answer is 100.

Note: It is easiest to see that we are adding 100 ones by looking at the sum of the positive even integers less than or equal to 200. There are 200/2 = 100 terms in this sum.

Quick solution: Once you get a little practice with this type of problem you can simply compute 100•1 = 100.

Solution using the sum feature on your graphing calculator: (This solution cannot be used on the GRE, but it could for other standardized tests where a graphing calculator is allowed) Press the 2nd button followed by the List button (same as Stat button).
Go to Math and select 5: sum( or press 5.
Press 2nd followed by List again.
Go to Ops and select 5: seq( or press 5.
Enter x, x, 1, 199, 2)).
The display should look like this: sum(seq(x, x, 1, 199, 2)).
Press Enter and you should get the answer 10,000.
Next enter sum(seq(x, x, 2, 200, 2)) and you should get the answer 10,100. Finally, 10,100 – 10,000 = 100.

Note: In the expression sum(seq(x, x, 2, 200, 2)) the last 2 indicates the step size. Here we are adding every other number.

3. The positive number k is the product of four different positive prime numbers. If the sum of these four prime numbers is a prime number greater than 20, what is the least possible value for k?

Solution: Let’s begin listing sequences of 4 prime numbers, and checking if their sum is also prime, beginning with the smallest primes.

2, 3, 5, 7          Sum = 17      too small
2, 3, 5, 11        Sum = 21      not prime
2, 3, 7, 11        Sum = 23      prime
2, 3, 5, 13        Sum = 23      prime

Now, (2)(3)(7)(11) = 462, and (2)(3)(5)(13) = 390. Since 390 is smaller,  k = 390.

More Hard GRE Math Practice Problems

For many more hard GRE math problems like these, each with several fully explained solutions, check out 320 GRE Math Problems arranged by Topic and Difficulty Level. 

And if you think your friends would like to try these problems, please share:

Talk soon!

Hard GRE Math Arithmetic Problems

Hello everybody. I think it’s time for all of you to do a little more work. Here are three challenging Level 5 GRE arithmetic questions. Note that all three of these questions are free response questions (or grid-ins). Please feel free to post your solutions or attempted solutions in the comments below and we can discuss the best way to solve each of these problems. I will post full solutions tomorrow.

Level 5 GRE Arithmetic Problems

1. If n is a positive integer such that the units (ones) digit of n² + 4n is 7 and the units digit of n  is not 7, what is the units digit of n + 3?

2. The sum of the positive odd integers less than 200 is subtracted from the sum of the positive even integers less than or equal to 200. What is the resulting difference?

3. The positive number k is the product of four different positive prime numbers. If the sum of these four prime numbers is a prime number greater than 20, what is the least possible value for k?

More Hard GRE Math Practice Problems

For many more hard GRE math problems like these, each with several fully explained solutions, check out 320 GRE Math Problems arranged by Topic and Difficulty Level. 

And if you think your friends would like to try these problems, please share:

Talk soon!

Hard Remainder Problem with Solution

Today I will provide a solution for the difficult remainder problem I asked you to attempt yesterday. Once again, you may want to read some of my older posts about remainders before going over the solution here.  You can find those posts by using the following links:

Can We Solve Remainder Problems Without Using Long Division?

The Cyclical Nature of Remainders

Remainders in Disguise

And now here is the question once more, followed by a complete solution.

Level 6 Remainder Problem

Find the remainder when 2¹²⁰ is divided by 3.

Solution by recognizing a pattern: 

2¹ = 2, remainder = 2
2² = 4, remainder = 1
2³ = 8, remainder = 2
2⁴ = 16, remainder = 1
2⁵ = 32, remainder = 2
2⁶ = 64, remainder = 1
2⁷ = 128, remainder = 2

Note that we evaluated the first 7 powers of 2, and then gave each of the remainders upon division by 3.

For example, 16 = 3(5) + 1, and so the remainder when 16 is divided by 3 is 1.

Now simply observe that all even powers of 2 give a remainder of 1 when divided by 3. Therefore, the answer is 1.

Remark: So how do we know with absolute certainty that the pattern we produced will continue indefinitely? After all, isn’t it possible that the pattern can stop at any time? Just because a pattern holds for the first 7 positive integers, it may not necessarily still hold for the 8th positive integer, or any other integer thereafter. But in this case it does.

Let’s prove two more general theorems that will imply that the pattern holds.

Theorem 1: If an integer gives a remainder of 1 when divided by 3, then twice that integer gives a reminder of 2 when divided by 3.

Proof: Let n be an integer that gives a remainder of 1 when divided by 3.

Then there is an integer k such that n = 3k + 1.

So 2n = 2(3k + 1) = 6k + 2 = 3(2k) + 2.

Since 2k is an integer, we have shown that 2n gives a remainder of 2 when divided by 3.

Theorem 2: If an integer gives a remainder of 2 when divided by 3, then twice that integer gives a reminder of 1 when divided by 3.

Proof: Let n be an integer that gives a remainder of 2 when divided by 3.

Then there is an integer k such that n = 3k + 2.

So 2n = 2(3k + 2) = 6k + 4 = 6k + 3 + 1 = 3(2k + 1) + 1.

Since 2k + 1 is an integer, we have shown that 2n gives a remainder of 1 when divided by 3.

After going through the proofs of these theorems, you should reflect back and make sure you understand why these two theorems imply that the pattern holds.

More Remainder Practice Problems

Don’t forget to take a look at the Get 800 collection of test prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

Hard Remainder Problem

Students are always asking me to solve some difficult problems. Today I would like to give you a difficult remainder problem similar to one a student recently asked me about. Before attempting this problem you may want to read some of my older posts on remainders. You can find them by using the following links:

Can We Solve Remainder Problems Without Using Long Division?

The Cyclical Nature of Remainders

Remainders in Disguise

And now here is a challenging problem for you to try. This problem is probably a little more difficult than any that would actually show up on a standardized test, but it’s always worth struggling with these harder problems a bit to help raise your level of mathematical maturity. Feel free to post your attempted solutions in the comments. I will provide a complete solution tomorrow.

Level 6 Remainder Problem

Find the remainder when 2¹²⁰ is divided by 3.

More Remainder Practice Problems

Don’t forget to take a look at the Get 800 collection of test prep books.

If you think your friends would like to try this problem, please share:

Speak to you soon!

General Graphing Calculator Advice for the SAT/ACT

• I always recommend that you use a TI-84 or comparable graphing calculator for the SAT or ACT.
• It is important that you are comfortable with your calculator on test day, so make sure that you are consistently practicing with the calculator you plan to use.
• Make sure that your calculator has fresh batteries the day of the test. Nobody will supply a calculator for you if yours dies.
• You may have to switch between DEGREE and RADIAN modes during the test. If you are using a TI-84 (or equivalent) calculator press the MODE button and scroll down to the third line when necessary to switch between modes.

Graphing Calculator Features You Should Know for the SAT/ACT

Below are the most important things you should practice on your graphing calculator.

(1) Practice entering complicated computations in a single step, and know when to insert parentheses. In general, there are 4 instances when you should use parentheses in your calculator. Around numerators of fractions Around denominators of fractions Around exponents Whenever you actually see parentheses in the expression

• Around numerators of fractions
• Around denominators of fractions
• Around exponents
• Whenever you actually see parentheses in the expression

Examples: We will substitute a 5 in for x in each of the following examples.

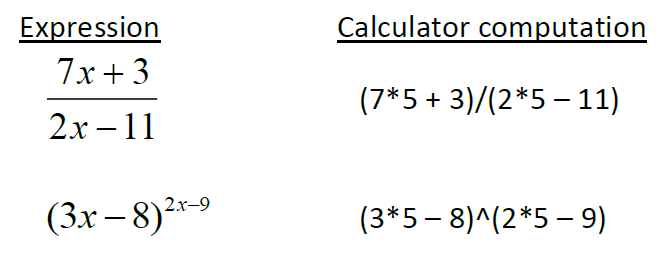
(2) Clear the screen before using it in a new problem. The big screen allows you to check over your computations easily.

(3) Press the ANS button (2^nd (-) ) to use your last answer in the next computation.

(4) Press 2^nd ENTER to bring up your last computation for editing. This is especially useful when you are plugging in answer choices, or guessing and checking.

(5) You can press 2^nd ENTER over and over again to cycle backwards through all the computations you have ever done.

(6) Know where the ,√ ,π and ^ buttons are so you can reach them quickly.

(7) Change a decimal to a fraction by pressing MATH ENTER ENTER.

(8) Press the MATH button – in the first menu that appears you can take cube roots and nth roots for any n.

(9) Know how to use the SIN, COS and TAN buttons as well as SIN^-1, COS^-1 and TAN^-1.

ACT only

The following features are necessary for the ACT only.

(10) Press the MATH button. Scroll right to NUM and you have lcm( and gcd(. Scroll right to PRB and you have nPr, nCr, and ! to compute permutations, combinations and factorials very quickly.

(11) Know where  LOG button is so you can reach it quickly.

Advanced Features

The following items are less important but can be useful for both the SAT and ACT.

(12) Press the Y= button to enter a function, and then hit ZOOM 6 to graph it in a standard window.

(13) Practice using the WINDOW button to adjust the viewing window of your graph.

(14) Practice using the TRACE button to move along the graph and look at some of the points plotted.

(15) Pressing 2nd TRACE (which is really CALC) will bring up a menu of useful items. For example selecting ZERO will tell you where the graph hits the x-axis, or equivalently where the function is zero. Selecting MINIMUM or MAXIMUM can find the vertex of a parabola. Selecting INTERSECT will find the point of intersection of 2 graphs.

And now it’s time to start practicing lots of math problems. For this you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

See you tomorrow!

Remainder Problems – Part 3

Welcome to the third and final part of this thread on remainder problems. In the first part we discussed some calculator algorithms for finding remainders. You can review that article here: SAT Remainder Problems – Part 1

Yesterday we discussed the cyclical nature of remainders. You can review that article here: SAT Remainder Problems – Part 2

I decided to spend three posts on this subject because many of my students in a mid-level scoring range seem to have a difficult time with ACT and GRE remainder questions.

Solution To Last Week’s Remainder Problem

So where were we? I left you with an ACT math problem to solve using the information I provided regarding the cyclical nature of remainders. Let’s find out how you did.

The problem again:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

Solution: We first find the least positive integer greater than 4 that is divisible by both 6 and 8. This is the least common multiple of 6 and 8 which is 24.

We now simply add the remainder.

24 + 4 = 28.

Thus, the answer is 28.

If you don’t know how to find the least common multiple of two numbers, it’s okay. If you’re taking the ACT, you can just let your TI-84 calculator do it for you. In your calculator press MATH, scroll right to NUM, and press 8 for lcm. Then type 6,8) and you will get an output of 24. So lcm(6,8)=24.

If you are taking the GRE, or you just want to learn other ways to compute the lcm, see the following article: Greatest Common Divisor (GCD) And Least Common Multiple (LCM)

Remainders In Disguise

Test makers’ love to put their remainder problems in disguise. In fact, many remainder problems on standardized tests do not even have the word “remainder” in the question! So how can you be expected to know when to find a remainder? The answer is quite simple. If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Remember this and you will recognize a remainder problem every time. In fact, this is such a key point I am going to repeat this in bold for you!

If the problem mentions some kind of sequence that keeps repeating over and over, then the problem may be asking you to find a remainder.

Let’s take a look at a standard example of such a question:

Example

Cards numbered from 1 through 2013 are distributed, one at a time, into nine stacks. The card numbered 1 is placed on stack 1, card number 2 on stack 2, card number 3 on stack 3, and so on until each stack has one card. If this pattern is repeated, each time beginning with stack one, on which stack will the card numbered 2013 be placed?

A. 3^rd stack
B. 4^th stack
C. 5^th stack
D. 6^th stack
E. 7^th stack

Solution: We are actually being asked to find the remainder when 2013 is divided by 9. Let’s do this using the first calculator algorithm that I showed you.

Step 1: Perform the division in your calculator

2013/9 ~ 223.667

Step 2: Multiply the integer part of this answer by the divisor:

9*223 = 2007

Step 3: Subtract this result from the dividend to get the remainder:

2013 – 2007 = 6.

So the card numbered 2013 will be placed on the 6^th stack, choice D.

Notice that the word remainder is never mentioned in this problem. The giveaway that this is a remainder problem in disguise is at the beginning of the last sentence where it says “If this pattern is repeated…”

So this is the end of this three part thread on remainders.

More Remainder Problems with Explanations

If you are preparing for the ACT, the GRE, or an SAT math subject test, you may want to take a look at one of the following books.

If you liked this article, please share it with your Facebook friends:

Remainder Problems – Part 2

Last week I introduced the idea of solving remainder problems without using long division. We may as well take advantage of the fact that we can use a calculator on the ACT (a TI-84 or equivalent) and GRE (the basic calculator they give you) to solve seemingly difficult math questions with ease. If you haven’t done so already, please read part 1 before continuing with this article: Remainder Problems – Part 1

Solution To Yesterday’s Problem

Yesterday I left you with a cliffhanger of a problem to solve with your calculator. Below is the solution. Let’s see if you got the problem correct and which method you used to solve the problem.

Here is the question again:

What is the remainder when 15,216 is divided by 73?

If you recall I gave three methods to solve such a problem, the first of which is by using long division. Since this post is about solving problems without using long division, let’s skip that method and jump straight to the much quicker and more efficient calculator algorithms – great for use on test day!

Method 2 – First Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Multiply the integer part of this answer by the divisor:

73*208 = 15,184

Step 3: Subtract this result from the dividend to get the remainder:

15,216 – 15,184 = 32.

And here is an alternative:

Method 3 – Second Calculator Algorithm:

Step 1: Perform the division in your calculator:

15,216/73 ~ 208.438

Step 2: Subtract off the integer part of this result:

ANS – 208 ~ .438

Step 3: Multiply this result by the divisor:

73*ANS = 32.

Did you get this problem correct? Which method did you use? Try using both methods and then choose the one that you will be most comfortable with on the day of your standardized math test. And remember: the best way to get comfortable with a new technique is to practice with it!

The Cyclical Nature Of Remainders

Today let’s talk a bit about the cyclical nature of remainders. If you can understand this, then solving many ACT and GRE remainder problems will become second nature to you.

Let’s see what happens when we divide various positive integers by the number 3.

When we divide 3 by 3 we get a quotient of 1 and a remainder of 0. In other words,

3 = 3(1) + 0.

When we divide 4 by 3 we get a quotient of 1 and a remainder of 1. In other words,

4 = 3(1) + 1.

When we divide 5 by 3 we get a quotient of 1 and a remainder of 2. In other words,

5 = 3(1) + 2.

Now we have to be careful. When we divide 6 by 3, the quotient is now 2 and the remainder is 0. That is, 6 = 3(2) + 0.

So the remainders start over. When dividing by 3, the remainders cycle from 0 to 2 then back to 0.

0, 1, 2, 0, 1, 2, 0, 1, 2…

The easiest way to find a positive integer that has a certain remainder is to start with one that is evenly divisible, and then add the remainder. For example, suppose we want to find a positive integer that has a remainder of 7 when divided by 9. We can start with a number evenly divisible by 9, such as 9 itself, and then add 7. Since 9 + 7 = 16, we see that 16 is such a number. In fact,

16 = 9(1) + 7.

That is, when we divide 16 by 9 the quotient is 1 and the remainder is 7.

Since 18 is also divisible by 9, 18 + 7 = 25 is another positive integer that has a remainder of 7 when divided by 9. There are infinitely many possibilities!

Note that 0 is actually divisible by 9 as well. Indeed, we have

0 = 9(0) + 0.

Thus, 0 + 7 = 7 is a number that gives a remainder of 7 when divided by 9. In other words, we can actually just use the remainder itself!

Exercise

Now let’s see if you can apply this information to an actual ACT math problem. Here is a nice medium difficulty problem I like to give to my own ACT math students:

What is the least positive integer greater than 4 that leaves a remainder of 4 when divided by both 6 and 8?

Do you know how to go about solving this? You can find the answer in part 3 of this article here: Remainder Problems – Part 3

More Remainder Problems with Explanations

If you are preparing for the ACT, the GRE, or an SAT math subject test, you may want to take a look at one of the following books.

And if you liked this article, please share it with your Facebook friends: