500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Right Triangle Trigonometry

Today I would like to begin talking about right triangle trigonometry. If you will be taking the ACT or one of the SAT math subject tests, and you are going for a very high score, then it is important that you understand the material covered here.

Let’s begin by focusing on angle A in the following picture: 

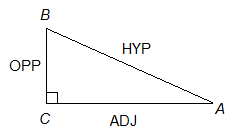
Note that the hypotenuse is ALWAYS the side opposite the right angle.

The other two sides of the right triangle, called the legs, depend on which angle is chosen. In this picture we chose to focus on angle A. Therefore the opposite side is BC, and the adjacent side is AC. 

Now you should simply memorize how to compute the six trig functions:

Here are a couple of tips to help you remember these:

(1) Many students find it helpful to use the word SOHCAHTOA. You can think of the letters here as representing sin, opp, hyp, cos, adj, hyp, tan, opp, adj.

(2) The three trig functions on the right are the reciprocals of the three trig functions on the left. In other words, you get them by interchanging the numerator and denominator. It’s pretty easy to remember that the reciprocal of tangent is cotangent. For the other two, just remember that the “s” goes with the “c” and the “c” goes with the “s.” In other words, the reciprocal of sine is cosecant, and the reciprocal of cosine is secant.

Note that if you are preparing for the ACT or Level 1 SAT math subject test, then it is not that important for you to know the reciprocal trig functions given in the right hand column, but it also couldn’t hurt to be somewhat familiar with them.

Example 1

To make sure you understand this, compute all six trig functions for each of the angles (except the right angle) in the triangle below.

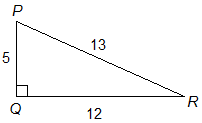
I suggest you try this yourself before looking at the answers:

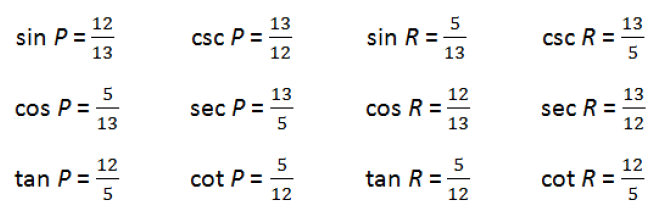
Example 2

In the right triangle pictured below, a, b, and c  and  are the lengths of its sides. What is the value of cos A ?

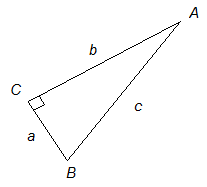
It’s quite easy if you know the rules.

Next week I will continue this thread by providing you with some more difficult examples.

More Trigonometry Practice Problems

If you are preparing for the ACT, SAT or an SAT math subject test, you may want to take a look at one of the books from the Get 800 collection of test prep books.

The Arithmetic Sequence Formula

Welcome back. Today I would like to conclude our discussion on arithmetic sequences that we began a few days ago. I recommend that you reread the first two posts on this topic before you move on to this one. Here are the links:

Arithmetic Sequences – Part One

Arithmetic Sequences – Part Two

Recall that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to give a very formal method for solving problems involving arithmetic sequences. Note that it is not necessary to learn this material in order to answer these types of questions on the ACT or SAT math subject tests, but every now and then the method given here gives a quicker way to solve a problem.

The arithmetic sequence formula

More advanced students may already know the arithmetic sequence formula:

In this formula a_n is the nth term of the sequence. For example, a₁ is the first term of the sequence.

Example 1

In the arithmetic sequence 20, 15, 10, 5, 0, -5, -10,… we have a₁ = 20 and d = -5. Therefore we have

So for example, the 50th term of this arithmetic sequence is

Let’s revisit the second example from last week, but this time we will give a solution using the arithmetic sequence formula.

Example 2

Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: Substituting 5 in for n and 33 in for a_n into the arithmetic sequence formula gives us

33 = a₁ + 4d.

Similarly, substituting 9 in for n and 97 in for a_n into the arithmetic sequence formula gives us

 97 = a₁ + 8d.

So we solve the following system of equations to find d.

97 = a₁ + 8d
33 = a₁ + 4d
64 =        4d

The last equation comes from subtraction. We now divide each side of this last equation by 4 to get

d = 16.

Finally, we add 16 to 97 three times to get 97 + 16(3) = 145.

Note that this solution is definitely more tedious than the previous solution from last week’s post. I usually prefer identifying arithmetic sequences with linear equations.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

Arithmetic Sequences and Linear Equations

Hello again. Today I would like to continue our discussion on arithmetic sequences from yesterday. I recommend that you reread yesterday’s post before you move on to this one. Here is the link: Arithmetic Sequences

Recall from last week that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to focus on the relationship between arithmetic sequences and linear equations.

Arithmetic sequences and linear equations

Recall the formula for the slope of a line:

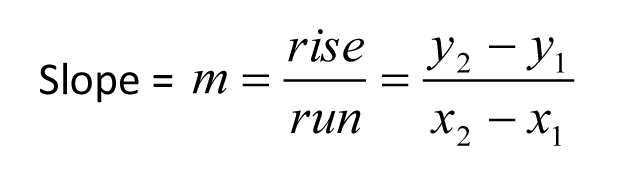
There is a natural correspondence between arithmetic sequences and linear equations. Each term of an arithmetic sequence can be naturally identified with a point on the corresponding line. Let’s go back to our first example of an arithmetic sequence from last week:

Example 1

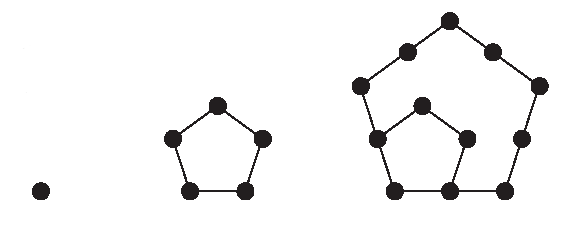
1, 4, 7, 10, 13, 16,…

We can identify terms of the sequence with points on a line where the x-coordinate is the term number and the y-coordinate is the term itself.

(1,1), (2,4), (3,7), (4,10), (5,13), (6,16),…

These points all lie on the same line, and we can compute the slope of this line by using any two of these points. For example, let’s use the points (2,4) and (6,16).

We have

m = (16 – 4)/(6 – 2) = 12/4 = 3

Do you recognize this number? That’s right! It’s the common difference of the sequence.

The identification of arithmetic sequences with linear equations gives us a nice method for finding the common difference of an arithmetic sequence as long as we know any 2 terms of the sequence.

Let’s try another example.

Example 2

Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: We identify the two given terms with the points (5,33) and (9,97). The common difference is then

d = (97 – 33)(9 – 5) = 64/4 = 16 

The twelfth term is then  97 + 16(3) = 145.

The information already covered in this post and the last is all you really need to know, but for completeness, tomorrow I’m going to talk about the arithmetic sequence formula.

More Problems Involving Arithmetic Sequences

If you are preparing for a standardized test, take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

And if you liked this article, please share it with your Facebook friends:

320 SAT Math Subject Test Problems – Huge Sale! 

Just $5.54 On Amazon

Today I would like to announce a huge sale on my book 320 SAT Math Subject Test Problems arranged by Topic and Difficulty Level for the Level 2 test.

The paperback is now on sale on Amazon for only $5.54.

This sale may last for only a few hours, and once the sale ends the price will go up to $34.99. Amazon will automatically raise the price once a predetermined number of copies has been sold. If you want to take advantage of the sale price I strongly recommend you purchase the book now.

Click the following link to get to the book’s Amazon page:

320 SAT Math Subject Test Problems – Level 2

As an extra incentive to buy this book from Amazon I want to offer you an additional book for FREE as a downloadable PDF file. You can choose ANY of my other books. So if you would like a different book, go ahead and purchase this one, forward me your Amazon confirmation email and let me know which of my books you would like for free. You will be provided with a link to download your additional free book. This offer is available until midnight of May 31, 2016.

You can forward your Amazon confirmation to

steve@SATPrepGet800.com

Take a look at my product page to see all of my books: Get 800 Product Page

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

Thank you all for your continued support!

Arithmetic Sequences

Hello everyone. Today I would like to talk about arithmetic sequences. Questions involving arithmetic sequences appear on the ACT, GRE and SAT math subject tests.  Here is an example of an arithmetic sequence.

Example 1

1, 4, 7, 10, 13, 16,…

Note that the first term of this sequence is 1, the second term of this sequence is 4, and so on.

So what makes this sequence arithmetic?

Well notice that to get from 1 to 4 we need to add 3. To get from 4 to 7 we also add 3. To get from 7 to 10 we also add 3. In other words, the sequence is arithmetic because we always add the same number to get from any term to the next term. This special number is called the common difference of the arithmetic sequence.

So why is this number called the common difference? Well another way to compute the common difference is to note that when we subtract any term from the next term we always get the same number, in this case that number is d = 3.

In other words we have 4 – 1 = 3, 7 – 4 = 3, and so on.

An arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence.

Let’s try a simple example.

Example 2

The second term of an arithmetic sequence is 15 and the third term is 10. What is the first term?

A.  –15
B.  –10
C.    1/15
D.    10
E.    20

Solution: Moving backwards, to get from the third term to the second term we add 5. Therefore we add 5 more to get to the first term. So the first term is

15 + 5 = 20.

This is choice E.

Note that in an arithmetic sequence, you always add (or subtract) the same number to get from one term to the next. This can be done by moving forwards or backwards through the sequence.

Note also that the common difference of this sequence is  d = 10 – 15 = –5.

Many students might mistakenly say that the common difference is 5.

This particular problem was pretty simple, so we were able to solve it just by “counting.” In other words we didn’t really have to worry about the formalities of whether the common difference was positive or negative. But in harder questions we might need to be more careful.

Alternate solution: Note that the terms of the sequence are getting smaller so that the first term must be larger than 15. So the answer must be choice E.

In my next post we will learn a special technique that makes many seemingly difficult problems involving arithmetic sequences very easy to solve. Check it out here: Arithmetic Sequences and Linear Equations

More Practice with Arithmetic Sequences

If you are preparing for a standardized test, you may want to take a look at the Get 800 collection of test prep books. Click on the picture below for more information.

 

Integers, Prime Numbers And Prime Factorizations

I would like to begin today with a few simple definitions of terms that appear in number theory problems on the ACT , GRE and SAT math subject tests.

Definitions

The integers are the counting numbers together with their negatives.

…,-4, -3, -2, -1, 0, 1, 2, 3, 4,…

The positive integers consist of the positive numbers from the above list.

1, 2, 3, 4,…

Next we have prime numbers.

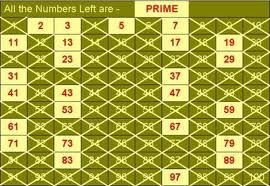
A prime number is a positive integer that has exactly two factors (1 and itself). Here is a list of the first few primes:

2, 3, 5, 7, 11, 13, 17, 19, 23,…

Note that 1 is not prime. It has only one factor.

A little trick:

Here is a quick trick for determining if a large number is prime: take the square root of the integer and check if the integer is divisible by each prime up to this square root. If not, the number is prime.

For example let’s try to figure out if 3001 is a prime number. Note that when we take the square root of 3001 in our calculator we get approximately 54.8. Now with our calculators we divide 3001 by 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, and 53 (all the prime numbers below 54.8). Since none of these are integers, 3001 is prime.

The Fundamental Theorem of Arithmetic

The fundamental theorem of arithmetic says “every integer greater than 1 can be written “uniquely” as a product of primes.”

The word “uniquely” is written in quotes because prime factorizations are only unique if we agree to write the primes in increasing order.

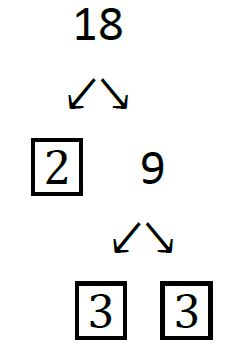
For example, 6 can be written as 2 · 3 or as 3 · 2. But these two factorizations are the same except that we changed the order of the factors. To make things as simple as possible we always agree to use the canonical representation. The word “canonical” is just a fancy name for “natural,” and the most natural way to write a prime factorization is in increasing order of primes. So the canonical representation of 6 is 2 · 3. As another example, the canonical representation of 18 is 2 · 3 · 3. We can tidy this up a bit by rewriting 3 · 3 as 3². So the canonical representation of 18 is 2 · 3². If you are new to factoring, you may find it helpful to draw a factor tree. For example here is a factor tree for 18:

To draw this tree we started by writing 18 as the product 2 · 9. We put a box around 2 because 2 is prime, and does not need to be factored anymore. We then proceeded to factor 9 as 3 · 3. We put a box around each 3 because 3 is prime. We now see that we are done, and the prime factorization can be found by multiplying all of the boxed numbers together. Remember that we will usually want the canonical representation, so write the final product in increasing order of primes.

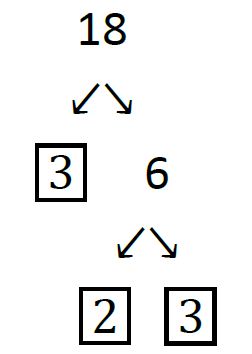
By the Fundamental Theorem of Arithmetic above it does not matter how we factor the number – we will always get the same canonical form. For example, here is a different factor tree for 18:

For practice, why don’t you try to draw a factor tree for 6137? Note that this is much more challenging than any number you will have to factor on a standardized test. I’ll have the solution for you tomorrow, so we can compare notes then. Remember, I am not looking for artistic merit – just make your factors clear in your drawing.

How many prime numbers are there?

This is going off on a bit of a tangent, but there are an infinite number of prime numbers. This was first proved by the ancient Greek mathematician Euclid.

Interestingly, the largest prime number found so far is  2^57,885,161 – 1. That’s a number with 17 million digits! I dare you to find the next one greater than that.

In the meantime, if you want to learn mathematical strategies to efficiently answer math questions on standardized tests, I would suggest that you take a look at the Get 800 collection of test prep books. Click on the picture below for more information about these books.

 

When to Use the Most Common Math Strategies

There are three very basic math strategies for standardized tests that every high school student should know: Plugging In Answer Choices, Taking Guesses, and Picking Numbers. Take a look at these links before you continue with this message, as the information below will make more sense after a quick review of these strategies.

Sometimes students get confused about when to use which of these strategies. Although there are no definite rules I can give you that will work 100 percent of the time, today I will provide you with some general guidelines.

Plugging In

Let’s begin with the strategy of plugging in answer choices:

This strategy can only be used for multiple choice questions. You simply plug each answer choice into the question until you find the one works. It is always best to start with choice C as your first attempt, unless there is a specific reason not to (on the new SAT you can start with choice B or C, as there are now just four choices). An example of such a reason would be that the word “least” appears in the problem. In this case start with the smallest answer choice (which will usually be choice A or E). Similarly, if the word greatest appears in the problem, start with the largest answer choice.

Plugging in can be used on problems from every topic and difficulty level. It’s often a great way to avoid having to perform messy algebra.

This strategy is most useful when the last part of the question says “What is_____” where the blank contains a single quantity.

Here are some examples:

(1) What is the value of x?
(2) What is the length of the original rectangle?
(3) What is the second number in the list?
(4) Which of the following is a perfect cube?
(5) What is the least such value of x?

For the first four of these examples you would start with choice C. For the fifth example you should start with the smallest answer choice.

This strategy is generally NOT useful when you are asked to find a more complicated expression. For example, do not try to plug in answer choices if the question ends with

“What is the value of x + y?”

In this case you will probably want to use the strategy of “Taking a guess,” or possibly “Picking numbers.”

During your SAT math practice sessions, you should try to apply this strategy on every multiple choice question. The more you attempt to use it, the easier it will be to detect when it can be applied.

Here is a straightforward example of a Level 1 Number Theory problem where “starting with choice C” is a useful strategy.

Three consecutive integers are listed in increasing order. If their sum is 138, what is the second integer in the list?

A. 45
B. 46
C. 47
D. 48
E. 49

I suggest you try to solve this problem in 3 ways:

• by starting with choice C
• algebraically
• using the fact that in a list of consecutive integers, the arithmetic mean is equal to the median.

And here is a Level 4 Geometry problem where this strategy is effective:

The sum of the areas of two squares is 85. If the sides of both squares have integer lengths, what is the least possible value for the length of a side of the smaller square?

A. 1
B. 2
C. 6
D. 7
E. 9

You should solve this problem by starting with choice A.

There are more examples in my original blog post titled Plugging in Answer Choices.

Taking Guesses

Next let’s talk about the strategy of taking a guess:

This strategy is similar to plugging in, except with this one you are not using the answer choices. The reason you are not using the answer choices is either because it is a grid in problem (so there are no answer choices), or the question is asking for a more complicated expression such as “the value of x + y,” or “the perimeter of a geometric figure.” In the first case you may want to take a guess for x or y, and in the second case you may want to take a guess for the width of a side of the figure. For examples of applying this strategy see my original blog post titled Taking A Guess. For a more difficult example, see my blog post titled Taking a Guess – A More Difficult Example.

Picking Numbers

And finally, let’s talk about the strategy of picking numbers:

This strategy is applied by choosing specific values for the unknown quantities in the problem. A new problem is formed that is easier to solve. After solving this easier problem, you must then plug the specific values you have picked into every answer choice, and eliminate any answer choices that do not come out correct. If more than one answer choice has not been eliminated, you can try picking new numbers to eliminate more choices.

Here are some occasions when the strategy of picking numbers will usually work:

• When one or more variables appear in the answer choices.
• When the word “percent” is in the problem (pick 100).
• When there is a variable in the problem, and it is implied that the answer does not depend on the value of the variable.

Here is an Algebra problem where “Picking numbers” can be used.

Which of the following is equal to (x + 66)/22 ?

A. (x+33)/11
B. x+3
C. 3x
D. x/22+3
E. (x+3)/11

Note that you usually want to avoid picking numbers that are too simple. For example, if you choose x = 0, then the answer to the question becomes 3. Now, if you plug a 0 in for x into every answer choice you get the following:

A. 3
B. 3
C. 0
D. 3
E. 3/11

Note that A, B and D are all correct.

See if you can solve this problem by picking a better number. You may also want to try to solve it algebraically.

For examples of applying this strategy see my original blog post on Picking Numbers.

Picking Numbers In Percent Problems

If the word “percent” appears in a problem it’s usually a great idea to choose the number 100. This often works even when there is no variable in the problem.

For examples of picking numbers in percent problems, see my blog post titled Picking Numbers In Percent Problems.

Summary

To summarize, here are some general guidelines for choosing which strategy to use:

• If the answer choices are all numbers, and you are being asked for a simple quantity, try plugging in first.
• If the answer choices are all numbers, and you are being asked for a more complicated quantity, try taking a guess.
• If the answer choices contain variables, try picking a number.
• Any question that mentions percents, pick the number 100.
• In grid in questions with variables, try taking a guess.

There is a lot of information in this blog post with links to many of my other posts, so take your time to read and digest the information. As always, the best way to internalize the concepts above is by practice. For daily practice you may want to check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

Plugging In Answer Choices

In many math problems on standardized tests such as the ACT, SAT, and GRE, you can get the answer simply by trying each of the answer choices until you find the one that works. Unless you have some intuition as to what the correct answer might be, then you should always start with choice C as your first guess (on the new SAT you can start with choice B or C because there are four choices instead of five). The reason for this is simple. Answers are usually given in increasing or decreasing order. So very often if choice C fails you can eliminate two of the other choices as well.

There are a few exceptions to this rule. If the word least appears in the problem, then start with the smallest number as your first guess. Similarly, if the word greatest appears in the problem, then start with the largest number as your first guess.

Examples

Let’s take a look at two math problems – one where we start with choice C and one where we do not.

Level 4 Geometry Question

When each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a side of the original square?

A) 3
B) 4
C) 5
D) 6
E) 7

Let’s start with choice (C). If the original length of a side of the square is 5, then the length becomes 8 when we increase it by 3. The original square has an area of 5²= 25 and the new square has area 8² = 64. So the area is increased by 64 – 25 = 39 square inches. Thus, we can eliminate choice (C), and most likely (A) and (B) as well.

We next try choice (D). We have 6² = 36, 9² = 81 and 81 – 36 = 45. Thus, the answer is choice (D).

Here is an algebraic solution for those of you that really want to see it.

Let x be the length, in inches, of a side of the original square. The length of a side of the new square is x + 3. The area of the original square is x², and the area of the new square is:

Thus, the answer is choice (D).

For this particular question, I prefer the solution by starting with choice C to the more tedious and confusing algebraic solution.

Level 3 Number Theory Question

What is the largest positive integer value of k for which 3^k divides 18⁴?

A) 2
B) 4
C) 6
D) 7
E) 8

Note: This type of question is no longer tested on the SAT, but it could show up on the ACT or GRE.

Pull out your calculator. Since the question has the word “largest” in it, we will start with the largest answer choice which is choice (E), and we will divide 18⁴ by 3⁸. We type 18^4 / 3^8 into our calculator and the output is 16. Since 16 is an integer, the answer is choice (E).

Note that all five answer choices give an integer, but 8 is the largest positive integer that works.

Here is a direct solution for those of you who really want to see it.

The prime factorization of 18 is 18 = 2·3². Therefore:

18⁴ = (2·3²)⁴ = 2⁴(3²)⁴ = 2⁴3⁸.

From this prime factorization it should be clear that 3⁸ divides 18⁴, but 3⁹ does not.

Again, for this particular question, most students will prefer the easier solution of starting with choice E (the largest answer choice) to the more confusing algebraic solution.

More Math Practice Problems

More information on this extremely useful strategy, as well as many more problems to practice with, can be found in the Get 800 collection of test prep books. Click on the picture below for more information about these books.

Plugging In – Part 1

 

Plugging In – Part 2

Speak to you soon!

Even and Odd Functions

A function f with the property that f(–x) = f(x) for all x is called an even function.

Example 1: f(x) = |x| is an even function because

f(–x) = |–x| = |x| = f(x).

A function f with the property that f(–x) = –f(x) for all x is called an odd function.

Example 2: g(x) = 1/x is odd because

g(–x) = 1/(–x) = –1/x = –g(x).

A polynomial function is a function for which each term has the form axⁿ where a is a real number and n is a positive integer.

Polynomial functions with only even powers of x are even functions. Keep in mind that a constant c is the same as cx⁰ , and so c is an even power of x.

Example 3: Here are some examples of polynomial functions that are even.

f(x) = x²

g(x) = 4

h(x) = 3x⁸ – 2x⁶+ 9

Polynomial functions with only odd powers of x are odd functions. Keep in mind that x is the same as x¹, and so x is an odd power of x.

Example 4: Here are some examples of polynomial functions that are odd.

f(x) = x³

g(x) = x

h(x) = 3x¹¹ – 2x⁵+ 9x

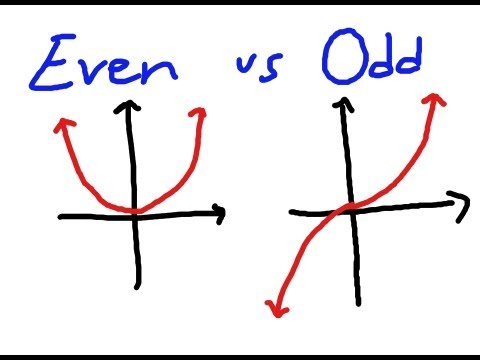
A quick graphical analysis of even and odd functions 

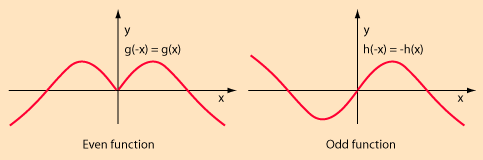
The graph of an even function is symmetrical with respect to the y-axis. This means that the y-axis acts like a “mirror,” and the graph “reflects” across this mirror.

The graph of an odd function is symmetrical with respect to the origin. This means that if you rotate the graph 180 degrees (or equivalently, turn it upside down) it will look the same as it did right side up.

So another way to determine if f(–x) = f(x) is to graph f in your graphing calculator, and see if the y-axis acts like a mirror (see the function g in the figure above).

Another way to determine if f(–x) = –f(x) is to graph f in your graphing calculator, and see if it looks the same upside down (see the function h in the figure above).

These two techniques will work for all functions (not just polynomials).

Check out the Get 800 collection of test prep books to learn how to apply this information to standardized test questions.

If you have any questions on this topic, then please post them in the comments below.

Speak to you soon!

Two Deadly Algebra Mistakes That You Need To Fix Right Now

Today I would like to go over two very common mistakes that students make when solving algebra problems that lead them to the wrong answer. These two errors are very basic and easily fixed. But surprisingly, even students in college calculus classes are still making these mistakes. Many students will make one of these mistakes on their SAT, ACT, or GRE, thus lowering their score. The good news is that if you just take a few minutes to read this article carefully, you will probably never make these two mistakes again. So please, don’t be another statistic. Read and absorb the information in this article right away. And if you want to discuss other common algebraic mistakes, please bring them up in the comments below.

Algebra Mistake Number 1

Let me start with a very simple math problem. What is –3² equal to?

Please take your time to answer this question yourself before looking at the answer.

Is the answer 9 or –9?

The answer is in fact –9.

Most of the time when I tell students the answer they say “but I thought when you square a negative number it becomes positive.”

And in fact, they are right. When you square a negative number it does become positive. But that is not what is going on here.

Don’t worry if you got this wrong. It does not mean you are not intelligent. It has nothing to do with your problem solving skills. It has only to do with a very small gap in knowledge which we will correct right now.

There are actually two issues that need to be addressed here.

Point 1: The first thing that you need to understand is that the expression –x is equivalent to the expression (–1)x. In other words, the operation of negation is equivalent to multiplication by –1.

Point 2: The second thing that you need to understand is the basic order of operations. In particular, exponentiation is always done before multiplication.

Note that the order of operations that we as humans currently use is a completely man-made construction. There is no really good reason that we do one operation before another one, except that a long time ago someone decided that this is the way we are going to do things.

So now, let’s get back to our computation.

By Point 1 above we have –3² = (–1)3². By Point 2, we must perform the exponentiation first. So we have –3² = (–1)3² =(–1)9 = –9.

Note: Although –3² = –9, we do have that (–3)² = 9. The reason is that in the latter case we are squaring a negative real number, and squaring a negative real number does always give a positive number.

Let’s try another example involving functions:

If f(x) = –x² + 5, then what is f(2)?

Solution: f(2) = –2² + 5 = –4 + 5 = 1.

Did you get that one correct? If not, reread this section until you can explain your error.

Try this similar question:

If f(x) = –x² + 5, then what is f(–2)?

Solution: f(–2) = –(–2)² + 5 = –4 + 5 = 1.

Note that the solution to this question is pretty much identical to the last one. This is because (–2)² is the same as 2². See the note above if you are still having trouble with this.

Algebra Mistake Number 2

Let’s look at another pretty basic math problem. Can you expand the expression –(x + 2)?

Again, please take your time to answer this question yourself before looking at the answer.

Did you get –x + 2, or –x – 2 ?

The answer is in fact –x – 2.

When negating an expression with two terms, many students forget to distribute the minus sign correctly.  In this case, both terms need to be negated.

If it helps you, you can rewrite –(x + 2) as (–1)(x + 2). Then we get

(–1)x + (–1)2 = –x – 2.

If you are okay with distributing in general, but only have trouble with this specific instance, then this might help. If this doesn’t help, then you need to go over the distributive property very carefully.

As another example, try to simplify this expression:

(x – 3) – (x – 5)

Let’s begin by removing the parentheses and distributing the subtraction symbol in the middle correctly:

x – 3 – x + 5

Finally we combine like terms to get an answer of 2.

Avoid Making Other Common Mistakes On Standardized Tests

If you want to learn how to avoid all the traps that occur in the math sections on standardized tests such as the SAT, ACT, and GRE, as well as learn all the most important math strategies, then take a look at the Get 800 collection of test prep books.  Click on the picture below for more information about these books.

If you have any questions on this topic, then please post them in the comments below.

Speak to you soon!