500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

More Arithmetic Sequences

Welcome back. Today I would like to conclude our discussion on arithmetic sequences that we began two weeks ago. I recommend that you reread the first two posts on this topic before you move on to this one. Here are the links:

Arithmetic Sequences – Part One

Arithmetic Sequences – Part Two

Recall that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to give a very formal method for solving problems involving arithmetic sequences. Note that it is not necessary to learn this material in order to answer these types of questions on the ACT or SAT, but every now and then the method given here gives a quicker way to solve a problem.

The arithmetic sequence formula

More advanced students may already know the arithmetic sequence formula:

In this formula a_n is the nth term of the sequence. For example, a₁ is the first term of the sequence.

Example 1:

In the arithmetic sequence 20, 15, 10, 5, 0, -5, -10,… we have a₁ = 20 and d = -5. Therefore we have

So for example, the 50th term of this arithmetic sequence is

Let’s revisit the second example from last week, but this time we will give a solution using the arithmetic sequence formula.

Example 2:

2. Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: Substituting 5 in for n and 33 in for a_n into the arithmetic sequence formula gives us

33 = a₁ + 4d.

Similarly, substituting 9 in for n and 97 in for a_n into the arithmetic sequence formula gives us

 97 = a₁ + 8d.

So we solve the following system of equations to find d.

97 = a₁ + 8d
33 = a₁ + 4d
64 =        4d

The last equation comes from subtraction. We now divide each side of this last equation by 4 to get

d = 16.

Finally, we add 16 to 97 three times to get 97 + 16(3) = 145.

Note that this solution is definitely more tedious than the previous solution from last week’s post. I usually prefer identifying arithmetic sequences with linear equations.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Arithmetic Sequences Continued

Hello again. Today I would like to continue our discussion on arithmetic sequences from last week. I recommend that you reread last week’s post before you move on to this one. Here is the link: Arithmetic Sequences

Recall from last week that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to focus on the relationship between arithmetic sequences and linear equations.

Arithmetic sequences and linear equations

Recall the formula for the slope of a line:

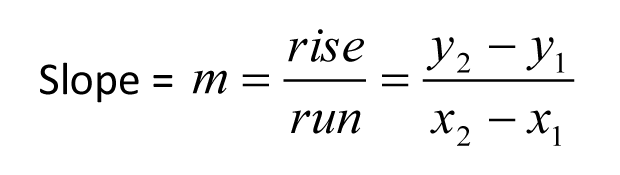
There is a natural correspondence between arithmetic sequences and linear equations. Each term of an arithmetic sequence can be naturally identified with a point on the corresponding line. Let’s go back to our first example of an arithmetic sequence from last week:

Example 1:

1, 4, 7, 10, 13, 16,…

We can identify terms of the sequence with points on a line where the x-coordinate is the term number and the y-coordinate is the term itself.

(1,1), (2,4), (3,7), (4,10), (5,13), (6,16),…

These points all lie on the same line, and we can compute the slope of this line by using any two of these points. For example, let’s use the points (2,4) and (6,16).

We have

Do you recognize this number? That’s right! It’s the common difference of the sequence.

The identification of arithmetic sequences with linear equations gives us a nice method for finding the common difference of an arithmetic sequence as long as we know any 2 terms of the sequence.

Let’s try another example.

Example 2:

2. Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: We identify the two given terms with the points (5,33) and (9,97). The common difference is then

The twelfth term is then  97 + 16(3) = 145.

 

The information already covered in this post and the last is all you really need to know, but for completeness, next week I’m going to talk about the arithmetic sequence formula.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Arithmetic Sequences

Hello everyone. Today I would like to talk about arithmetic sequences. Questions involving arithmetic sequences appear all the time on the ACT and SAT math subject tests, and once in a while on the SAT.  Here is an example of an arithmetic sequence.

Example 1:

1, 4, 7, 10, 13, 16,…

Note that the first term of this sequence is 1, the second term of this sequence is 4, and so on.

So what makes this sequence arithmetic?

Well notice that to get from 1 to 4 we need to add 3. To get from 4 to 7 we also add 3. To get from 7 to 10 we also add 3. In other words, the sequence is arithmetic because we always add the same number to get from any term to the next term. This special number is called the common difference of the arithmetic sequence.

So why is this number called the common difference? Well another way to compute the common difference is to note that when we subtract any term from the next term we always get the same number, in this case that number is d = 3.

In other words we have 4 – 1 = 3, 7 – 4 = 3, and so on.

An arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence.

Let’s try a simple example.

Example 2:

2. The second term of an arithmetic sequence is 15 and the third term is 10. What is the first term?

 

Solution: Moving backwards, to get from the third term to the second term we add 5. Therefore we add 5 more to get to the first term. So the first term is

15 + 5 = 20.

This is choice E.

Note that in an arithmetic sequence, you always add (or subtract) the same number to get from one term to the next. This can be done by moving forwards or backwards through the sequence.

Note also that the common difference of this sequence is  d = 10 – 15 = –5.

Many students might mistakenly say that the common difference is 5.

This particular problem was pretty simple, so we were able to solve it just by “counting.” In other words we didn’t really have to worry about the formalities of whether the common difference was positive or negative. But in harder questions we might need to be more careful.

Alternate solution: Note that the terms of the sequence are getting smaller so that the first term must be larger than 15. So the answer must be choice E.

In my next post we will learn a special technique that makes many seemingly difficult problems involving arithmetic sequences very easy to solve. So please check back next week.

More Practice with Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Two Deadly Algebra Mistakes

Today I would like to go over two very common mistakes that students make when solving algebra problems that lead them to the wrong answer. These two errors are very basic and easily fixed. But surprisingly, even students in college calculus classes are still making these mistakes. Many students will make one of these mistakes on their SAT or ACT, thus lowering their score. The good news is that if you just take a few minutes to read this article carefully, you will probably never make these two mistakes again. So please, don’t be another statistic. Read and absorb the information in this article right away. And if you want to discuss other common algebraic mistakes, please bring them up in the comments below.

Algebra Mistake Number 1:

Let me start with a very simple math problem. What is –3² equal to?

Please take your time to answer this question yourself before looking at the answer.

Is the answer 9 or –9?

The answer is in fact –9.

Most of the time when I tell students the answer they say “but I thought when you square a negative number it becomes positive.”

And in fact, they are right. When you square a negative number it does become positive. But that is not what is going on here.

Don’t worry if you got this wrong. It does not mean you are not intelligent. It has nothing to do with your problem solving skills. It has only to do with a very small gap in knowledge which we will correct right now.

There are actually two issues that need to be addressed here.

Point 1: The first thing that you need to understand is that the expression –x is the same as (–1)x. In other words, the operation of negation is equivalent to multiplication by –1.

Point 2: The second thing that you need to understand is the basic order of operations. In particular, exponentiation is always done before multiplication.

Note that the order of operations that we as humans currently use is a completely man-made construction. There is no really good reason that we do one operation before another one, except that a long time ago someone decided that this is the way we are going to do things.

So now, let’s get back to our computation.

By Point 1 above we have –3² = (–1)3². By Point 2, we must perform the exponentiation first. So we have –3² = (–1)3² =(–1)9 = –9.

Note: Although –3² = –9, we do have that (–3)² = 9. The reason is that in the latter case we are squaring a negative real number, and squaring a negative real number does always give a positive number.

Let’s try another example involving functions:

If f(x) = –x² + 5, then what is f(2)?

Solution: f(2) = –2² + 5 = –4 + 5 = 1.

Did you get that one correct? If not, reread this section until you can explain your error.

Try this similar question:

If f(x) = –x² + 5, then what is f(–2)?

Solution: f(–2) = –(–2)² + 5 = –4 + 5 = 1.

Note that the solution to this question is pretty much identical to the last one. This is because (–2)² is the same as 2². See the note above if you are still having trouble with this.

Algebra Mistake Number 2:

Let’s look at another pretty basic math problem. Can you expand the expression –(x + 2)?

Again, please take your time to answer this question yourself before looking at the answer.

Did you get –x + 2, or –x – 2 ?

The answer is in fact –x – 2.

When negating an expression with two terms, many students forget to distribute the minus sign correctly.  In this case, both terms need to be negated.

If it helps you, you can rewrite –(x + 2) as (–1)(x + 2). Then we get

(–1)x + (–1)2 = –x – 2.

If you are okay with distributing in general, but only have trouble with this specific instance, then this might help. If this doesn’t help, then you need to go over the distributive property very carefully.

As another example, try to simplify this expression:

(x – 3) – (x – 5)

Let’s begin by removing the parentheses and distributing the subtraction symbol in the middle correctly:

x – 3 – x + 5

Finally we combine like terms to get an answer of 2.

Avoid Making Other Common Mistakes On the SAT

If you want to learn how to avoid all the traps that occur in the math sections of the SAT, as well as learn all the most important SAT math strategies, then take a look at my 28 SAT Math Lessons Series. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the comments below.

Speak to you soon!

Right Triangle Trigonometry – Part 2

Last week I began going over the fundamentals of right triangle trigonometry. I suggest that you review the material in that post before continuing on with this one. You can find that post here: Right Triangle Trigonometry – Part 1

Let’s quickly review the six basic trigonometric functions: 

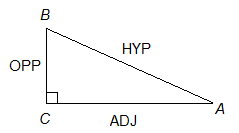
Very often in trigonometry problems on standardized tests the Pythagorean Theorem is needed to get the final answer.

The Pythagorean Theorem: If a right triangle has legs of length a and b, and a hypotenuse of length c, then c² = a² + b².

Example 3:

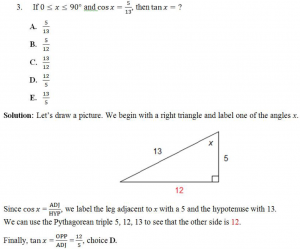
Notes: (1) The most common Pythagorean triples are 3,4,5 and 5, 12, 13. Two others that may come up are 8, 15, 17 and 7, 24, 25.

(2) If you don’t remember the Pythagorean triple 5, 12, 13, you can use the Pythagorean Theorem:

Here we have 5² + b² = 13². Therefore 25 + b² = 169. Subtracting 25 from each side of this equation gives b² = 169 – 25 = 144. So b = 12.

(3) The equation b² = 144 would normally have solutions b = 12 and b = –12. But the length of a side of a triangle cannot be negative, so we reject –12.

More Trigonometry Practice Problems

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Speak to you soon!