act math prep Archives - Page 2 of 3

500 New SAT Math Problems – Just 19.99 Today Only

June 30, 2024

$500 New SAT Math Problems$

500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

~~The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99.~~

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

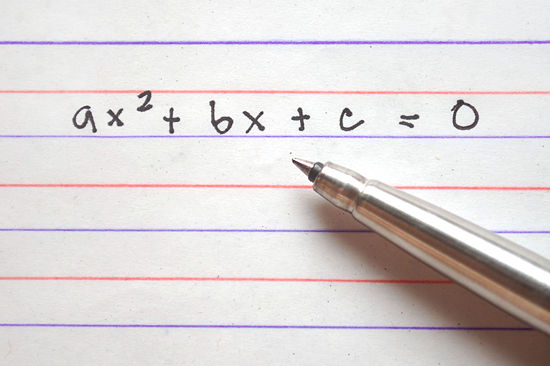
Hard SAT and ACT Math Problem with Solution – Quadratic Equations

November 16, 2016

Hard SAT and ACT Math Problem with Solution

Quadratic Equations

Today I would like to provide a solution to yesterday’s hard math problem involving quadratic equations. Here is the problem once again, followed by a solution.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x²– 70x + 25 = 0
B. 49x²+ 70x + 25 = 0
C. 49x²+ 35x + 25 = 0
D. 49x²+ 25 = 0
E. 49x²– 25 = 0

* If -5/7 is the only solution, then x + 5/7 is the only factor (by the factor theorem). So we have

(x + 5/7)(x + 5/7) = 0

x² + 5/7 x + 5/7 x + (5/7)² = 0

x² + 10/7 x + 25/49 = 0

49x² + 70x + 25 = 0

This is choice B.

Notes: (1) The factor theorem says that r is a root of the polynomial p(x) if and only if x – r is a factor of the polynomial.

(2) In factored form, a quadratic equation always has two factors. Since x + 5/7 is the only factor in this problem, it must appear twice.

(3) In going from the first equation to the second equation, we multiplied the two polynomials (x + 5/7 times itself). To do this you can use FOIL or any other method you like for multiplying polynomials.

(4) In going from the second equation to the third equation, we simply added 5/7 x + 5/7 x = 10/7 x.

(5) In going from the third equation to the last equation, we multiplied both sides of the equation by the least common denominator, which is 49. More precisely, on the left hand side we have

49(x² +10/7 x + 25/49)

= 49x² + 49(10/7 x) + 49(25/49)

= 49x² +7(10x) + 25

= 49x² +70x + 25.

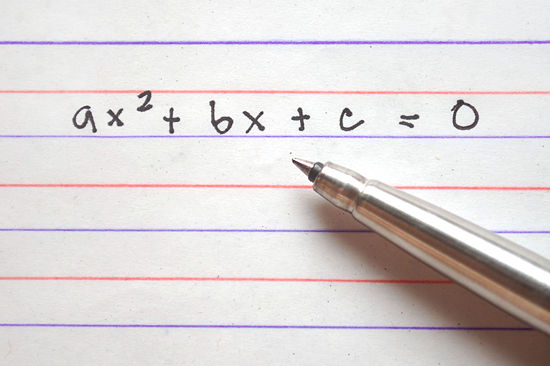
Hard SAT and ACT Math Problem

Quadratic Equations

Today I would like to give a hard math problem involving quadratic equations. This question type can show up on both the SAT and ACT. I will provide a full explanation for this problem soon. Feel free to leave your own solutions in the comments.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x²– 70x + 25 = 0
B. 49x²+ 70x + 25 = 0
C. 49x²+ 35x + 25 = 0
D. 49x²+ 25 = 0
E. 49x²– 25 = 0

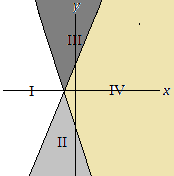
Hard SAT and ACT Math Problem with Solution

System of Inequalities

Today I would like to provide a solution to yesterday’s SAT/ACT problem involving a system of inequalities. Here is the problem once again, followed by a solution.

Level 5 System of Inequalities

y ≤ 2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

Solution: The line y = 2x + 2 has a slope of 2 > 0, and therefore the graph is the line that moves upwards as it is drawn from left to right.

The point (0,0) satisfies the inequality y ≤ 2x + 2 since 0 ≤ 2(0) + 2, or equivalently 0 ≤ 2 is true.

It follows that the graph of y ≤ 2x + 2 consists of sections II and IV.

The line y = –3x – 3 has a slope of –3 < 0, and therefore the graph is a line that moves downwards as it is drawn from left to right.

(0,0) satisfies the inequality y ≥ –3x – 3 since 0 ≥ –3(0) – 3, or equivalently 0 ≥ –3 is true.

It follows that the graph of y ≥ –3x – 3 consists of sections III and IV.

The intersection of the two solution graphs is section IV, choice B.

Note: For a more detailed explanation, see 28 New SAT Math Lessons – Advanced Course

Hard SAT and ACT Math Problem

System of Inequalities

Today I would like to give a hard math problem involving a system of inequalities. This type of question can show up on both the SAT and ACT. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 5 System of Inequalities

y ≤ 2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

Increasing Your SAT Math Score from 750 to 800

Recently I’ve been getting emails from students that are already scoring over 700 in math on SAT practice tests, but they are still struggling to get a perfect score. First, I’d like to point out that if you are already close to the mid 700’s, then there aren’t any universities that will exclude you based on your SAT math score. On the other hand, I do realize that there are many students out there that would still love to get a perfect score anyway.

The video above shows me completing an SAT math section perfectly in about one-third the time given. Even though this video was for the old SAT, if you are above a 700 in SAT math, it’s worth watching so you can compare what I’m doing to what you’re doing. I also have videos for the other two sections at the bottom of this post.

If you’re one of those students that is struggling to get those last few hard questions right, you may want to take a look at the following article: Stop Getting Those Last Few Hard SAT Math Questions Wrong

If you’re still making careless errors on some of the easier problems, then take a look here: Stop Making Careless Errors in SAT Math

Another possibility is that you’re running out of time, and you don’t have time to catch a careless error or two that you’re still making. Here are some long-term strategies for getting you to increase your speed without feeling rushed.

Don’t just try to solve each problem, figure out how many ways you can solve each problem – using multiple methods multiplies the value you get out of each problem.
After trying to solve each problem several different ways, ask yourself questions about each method: Which one was quickest for you? Which one should have been the quickest, if only you were better at it? Which one guarantees the right answer? Which one was tricky, but more effective once you got the hang of it.
Internalize strategies and methods – don’t just practice them, try to get to a point where they become a part of you.

The goal is to decrease the amount of time spent on each problem by knowing which method to use right away, and having practiced the method enough so that you can arrive at an answer fairly quickly. Never try to decrease the amount of time by physically speeding up! The speed will come with practice, internalizing the strategies, and gaining enough intuition to choose the best method for each individual problem.

The journey from a 750 to an 800 requires some time, some effort, and a lot of practice. Understanding strategies, concepts and methods is no longer enough – you have to make them a part of you so that the ideas form before you even have a chance to think about them. This requires a jump in your level of mathematical maturity. The good news is that if you put in the effort to do this now, then that experience will stay with you, and it will even make your college classes much easier.

SAT Math Practice Problems

For daily SAT math practice, check out the Get 800 collection of SAT math books. Click on the picture below for more information about these books.

And if you liked this article, please share it with your Facebook friends:

Hard ACT Math Probability Problem with Solution

August 20, 2016

Hard ACT Math Probability Problem with Solution

Today I will give a solution to yesterday’s ACT math probability problem. Here is the question again followed by a ful solution.

Level 5 Probability

Suppose that x will be randomly selected from the set

{–3/2, –1, –1/2, 0, 5/2}

and that y will be randomly selected from the set

{–3/4, –1/4, 2, 11/4}.

What is the probability that x/y < 0 ?

A. 1/100
B. 1/20
C. 3/20
D. 1/3
E. 2/5

Solution: There are 5 possible values for x and 4 possible values for y. By the counting principle, there are 5 ⋅ 4 = 20 possibilities for xy (possibly with some repetition).

In order for x/y < 0 to be true, x and y need to be opposite in sign. The number of ways for this to happen (possibly with repetition) is

3 ⋅ 2 + 1 ⋅ 2 = 6 + 2 = 8

So the desired probability is 8/20 = 2/5, choice E.

Notes: (1) In this question when we mention the possibilities for xy, we are ignoring the fact that there could be repeated values. For example, we have (0)(–3/4) = 0 and (0)(–1/4) = 0. Technically these two computations give a single value for xy. Nonetheless, to compute the desired probability we need to think of these as distinct possibilities.

(2) There are 3 negative values for x and 2 positive values for y. This gives us 3 ⋅ 2 = 6 negative values for xy.

There is 1 positive value for x and 2 negative values for y. This gives us 1 ⋅ 2 = 2 more negative values for xy.

So altogether there are 6 + 2 = 8 possibilities that lead to a negative value for xy.

Hard ACT Math Probability Problem

Today I would like to give a hard ACT math probability problem. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 5 Probability

Suppose that x will be randomly selected from the set

{–3/2, –1, –1/2, 0, 5/2}

and that y will be randomly selected from the set

{–3/4, –1/4, 2, 11/4}.

What is the probability that x/y < 0 ?

A. 1/100
B. 1/20
C. 3/20
D. 1/3
E. 2/5

ACT Math Number Theory Problem with Solutions

Today I will give a solution to yesterday’s ACT math number theory problem. Here is the question one more time followed by a full solution.

Level 3 Number Theory

What positive number when divided by its reciprocal has a result of 9/16?

A. 8/3
B. 3/8
C. 4/3
D. 3/16
E. 3/4

Solution by starting with choice C: Let’s start with 4/3 as our first guess. The reciprocal of 4/3 is 3/4, and when we divide 4/3 by 3/4, we get 16/9. This is not correct, but it is the reciprocal of what we are trying to get. So the answer is the reciprocal of 4/3, which is 3/4, choice E.

Notes: (1) The reciprocal of the fraction a/b is the fraction b/a. In other words, we get the reciprocal of the fraction by interchanging the number on top (the numerator) with the number on bottom (the denominator).

(2) We can divide 4/3 by 3/4 right in our TI-84 calculator by typing

(4 / 3) / (3 / 4) ENTER MATH ENTER ENTER

The output will be 16/9.

Pressing MATH ENTER ENTER at the end changes the decimal to a fraction.

(3) We can also do the computation by hand as follows:

$\frac{4}{3}\div\frac{3}{4}= \frac{4}{3}\cdot\frac{4}{3}= \frac{4\cdot 4}{3\cdot 3}=\frac{16}{9}$

(4) Let’s also just confirm that choice E is the answer. I’ll use the hand method, but you can also feel free to use your calculator.

$\frac{3}{4}\div\frac{4}{3}= \frac{3}{4}\cdot\frac{3}{4}= \frac{3\cdot 3}{4\cdot 4}=\frac{9}{16}$

* Algebraic solution: Let x be the positive number. We are given that

$x\div \frac{1}{x}=\frac{9}{16}$

$\frac{x\cdot x}{1}=\frac{9}{16}$

$x\cdot x=\frac{9}{16}$

$x^2=\frac{9}{16}$

$x=\pm \sqrt{\frac{9}{16}}=\pm \frac{\sqrt{9}}{\sqrt{16}}=\pm \frac{3}{4}$

Since we are given that x is a positive number, x = 3/4, choice E.

ACT Math Number Theory Problem

Today I would like to give an ACT math number theory problem. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 3 Number Theory

What positive number when divided by its reciprocal has a result of 9/16?

A. 8/3
B. 3/8
C. 4/3
D. 3/16
E. 3/4

The Arithmetic Sequence Formula

Welcome back. Today I would like to conclude our discussion on arithmetic sequences that we began a few days ago. I recommend that you reread the first two posts on this topic before you move on to this one. Here are the links:

Arithmetic Sequences – Part One

Arithmetic Sequences – Part Two

Recall that an arithmetic sequence is a sequence of numbers such that the difference between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to give a very formal method for solving problems involving arithmetic sequences. Note that it is not necessary to learn this material in order to answer these types of questions on the ACT or SAT math subject tests, but every now and then the method given here gives a quicker way to solve a problem.

The arithmetic sequence formula

More advanced students may already know the arithmetic sequence formula:

$a_n=a_1+(n-1)d$

In this formula a_n is the nth term of the sequence. For example, a₁ is the first term of the sequence.

Example 1

In the arithmetic sequence 20, 15, 10, 5, 0, -5, -10,… we have a₁= 20 and d = -5. Therefore we have

$a_n=20+(n-1)(-5)=20-5n+5=25-5n$

So for example, the 50th term of this arithmetic sequence is

$a_{50}=25-5(50)=-225$

Let’s revisit the second example from last week, but this time we will give a solution using the arithmetic sequence formula.

Example 2

Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: Substituting 5 in for n and 33 in for a_n into the arithmetic sequence formula gives us

33 = a₁ + 4d.

Similarly, substituting 9 in for n and 97 in for a_n into the arithmetic sequence formula gives us

97 = a₁ + 8d.

So we solve the following system of equations to find d.

97 = a₁ + 8d
33 = a₁ + 4d
64 = 4d

The last equation comes from subtraction. We now divide each side of this last equation by 4 to get

d = 16.

Finally, we add 16 to 97 three times to get 97 + 16(3) = 145.

Note that this solution is definitely more tedious than the previous solution from last week’s post. I usually prefer identifying arithmetic sequences with linear equations.

$500 New SAT Math Problems$