500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Hello everyone.

I have already spoken about solving algebraic equations both informally and formally in the past. The original article is here: Informal and Formal Algebra

Today I have uploaded a video to my YouTube channel that shows how to apply the strategy of “picking numbers” to ACT math problems. You can visit the YouTube page here: ACT Prep – Informal and Formal Algebra

For your convenience I have also embedded this video below:

If you liked this video, please share it with your Facebook friends:

Until next time…

The Contrapositive

A statement of the form “if p, then q” is known as a conditional statement. An example of such a statement is “If you are a cat, then you have fur.” Another common way to say this is “All cats have fur.”

There are 3 other statements that often come up in association with a conditional statement. Let’s use the example above to illustrate.

Conditional: If you are a cat, then you have fur.
Converse: If you have fur, then you are a cat.
Inverse: If you are not a cat, then you do not have fur.
Contrapositive: If you do not have fur, then you are not a cat.

The most important thing to know for the SAT is that the contrapositive is logically equivalent to the original conditional statement! The converse and inverse are not.

For example, suppose the conditional statement “All cats have fur” is true. You may want to rewrite this as “If you are a cat, then you have fur.” It follows that “If you do not have fur, then you are not a cat” is also true.

In particular, if you are given the statement “Skittles does not have fur,” you can infer “Skittles is not a cat.”

Note that neither the converse nor the inverse is logically equivalent to the original conditional statement, but they are equivalent to each other.

Example 1

1. If the statement above is true, which of the following statements must also be true?(A) If John cannot ski, then he is not Jim’s friend
   (B) If Jeff can ski, then he is not Jim’s friend.
   (C) If Joseph can ski, then he is Jim’s friend.
   (D) If James is Jim’s friend, then he cannot ski.
   (E) If Jordan is not Jim’s friend, then he cannot ski.

Solution: The given statement can be written in conditional form as “If you are Jim’s friend, then you can ski.” The contrapositive of this statement is “If you cannot ski, then you are not Jim’s friend. Replacing “you” with “John” gives the correct answer as choice (A).

Example 2

If the statement above is true, which of the following statements must also be true?

(A) If a beverage is listed in menu B, it is also in menu A.
(B) If a beverage is not listed in menu A, it is not listed in menu B.
(C) If a beverage is not listed in menu B, it is not listed in menu A.
(D) If a beverage is not listed in menu B, it is in menu A.
(E) If a beverage is listed in menu B, it is not listed in menu A.

Solution: Simply observe that the statement in choice (C) is the contrapositive of the given statement. So the answer is choice (C).

Conclusion

If you understand how to identify the contrapositive of a conditional statement, then you will be able to easily get most logic questions correct that appear on the SAT.  There are a couple of other types of logic questions that can appear on the SAT. I will address those in a future blog post.

If you liked this article, please share it with your Facebook friends:

More Arithmetic Sequences

Welcome back. Today I would like to conclude our discussion on arithmetic sequences that we began two weeks ago. I recommend that you reread the first two posts on this topic before you move on to this one. Here are the links:

Arithmetic Sequences – Part One

Arithmetic Sequences – Part Two

Recall that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to give a very formal method for solving problems involving arithmetic sequences. Note that it is not necessary to learn this material in order to answer these types of questions on the ACT or SAT, but every now and then the method given here gives a quicker way to solve a problem.

The arithmetic sequence formula

More advanced students may already know the arithmetic sequence formula:

In this formula a_n is the nth term of the sequence. For example, a₁ is the first term of the sequence.

Example 1:

In the arithmetic sequence 20, 15, 10, 5, 0, -5, -10,… we have a₁ = 20 and d = -5. Therefore we have

So for example, the 50th term of this arithmetic sequence is

Let’s revisit the second example from last week, but this time we will give a solution using the arithmetic sequence formula.

Example 2:

2. Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: Substituting 5 in for n and 33 in for a_n into the arithmetic sequence formula gives us

33 = a₁ + 4d.

Similarly, substituting 9 in for n and 97 in for a_n into the arithmetic sequence formula gives us

 97 = a₁ + 8d.

So we solve the following system of equations to find d.

97 = a₁ + 8d
33 = a₁ + 4d
64 =        4d

The last equation comes from subtraction. We now divide each side of this last equation by 4 to get

d = 16.

Finally, we add 16 to 97 three times to get 97 + 16(3) = 145.

Note that this solution is definitely more tedious than the previous solution from last week’s post. I usually prefer identifying arithmetic sequences with linear equations.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Arithmetic Sequences Continued

Hello again. Today I would like to continue our discussion on arithmetic sequences from last week. I recommend that you reread last week’s post before you move on to this one. Here is the link: Arithmetic Sequences

Recall from last week that an arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence. In this post I would like to focus on the relationship between arithmetic sequences and linear equations.

Arithmetic sequences and linear equations

Recall the formula for the slope of a line:

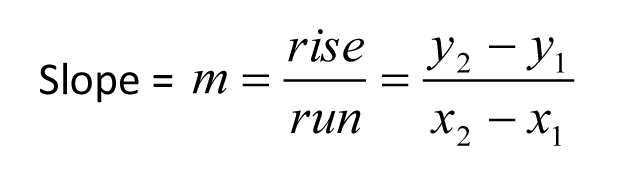
There is a natural correspondence between arithmetic sequences and linear equations. Each term of an arithmetic sequence can be naturally identified with a point on the corresponding line. Let’s go back to our first example of an arithmetic sequence from last week:

Example 1:

1, 4, 7, 10, 13, 16,…

We can identify terms of the sequence with points on a line where the x-coordinate is the term number and the y-coordinate is the term itself.

(1,1), (2,4), (3,7), (4,10), (5,13), (6,16),…

These points all lie on the same line, and we can compute the slope of this line by using any two of these points. For example, let’s use the points (2,4) and (6,16).

We have

Do you recognize this number? That’s right! It’s the common difference of the sequence.

The identification of arithmetic sequences with linear equations gives us a nice method for finding the common difference of an arithmetic sequence as long as we know any 2 terms of the sequence.

Let’s try another example.

Example 2:

2. Each term of a certain sequence is greater than the term before it. The difference between any two consecutive terms in the sequence is always the same number. If the fifth and ninth terms of the sequence are 33 and 97, respectively, what is the twelfth term?

Solution: We identify the two given terms with the points (5,33) and (9,97). The common difference is then

The twelfth term is then  97 + 16(3) = 145.

The information already covered in this post and the last is all you really need to know, but for completeness, next week I’m going to talk about the arithmetic sequence formula.

More Problems Involving Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Arithmetic Sequences

Hello everyone. Today I would like to talk about arithmetic sequences. Questions involving arithmetic sequences appear all the time on the ACT and SAT math subject tests, and once in a while on the SAT.  Here is an example of an arithmetic sequence.

Example 1:

1, 4, 7, 10, 13, 16,…

Note that the first term of this sequence is 1, the second term of this sequence is 4, and so on.

So what makes this sequence arithmetic?

Well notice that to get from 1 to 4 we need to add 3. To get from 4 to 7 we also add 3. To get from 7 to 10 we also add 3. In other words, the sequence is arithmetic because we always add the same number to get from any term to the next term. This special number is called the common difference of the arithmetic sequence.

So why is this number called the common difference? Well another way to compute the common difference is to note that when we subtract any term from the next term we always get the same number, in this case that number is d = 3.

In other words we have 4 – 1 = 3, 7 – 4 = 3, and so on.

An arithmetic sequence is a sequence of numbers such that the difference  between consecutive terms is constant. The number d is called the common difference of the arithmetic sequence.

Let’s try a simple example.

Example 2:

2. The second term of an arithmetic sequence is 15 and the third term is 10. What is the first term?

Solution: Moving backwards, to get from the third term to the second term we add 5. Therefore we add 5 more to get to the first term. So the first term is

15 + 5 = 20.

This is choice E.

Note that in an arithmetic sequence, you always add (or subtract) the same number to get from one term to the next. This can be done by moving forwards or backwards through the sequence.

Note also that the common difference of this sequence is  d = 10 – 15 = –5.

Many students might mistakenly say that the common difference is 5.

This particular problem was pretty simple, so we were able to solve it just by “counting.” In other words we didn’t really have to worry about the formalities of whether the common difference was positive or negative. But in harder questions we might need to be more careful.

Alternate solution: Note that the terms of the sequence are getting smaller so that the first term must be larger than 15. So the answer must be choice E.

In my next post we will learn a special technique that makes many seemingly difficult problems involving arithmetic sequences very easy to solve. So please check back next week.

More Practice with Arithmetic Sequences

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them in the Get 800 ACT/SAT prep forum:

I will answer your questions right away.

Speak to you soon!

Right Triangle Trigonometry – Part 2

Last week I began going over the fundamentals of right triangle trigonometry. I suggest that you review the material in that post before continuing on with this one. You can find that post here: Right Triangle Trigonometry – Part 1

Let’s quickly review the six basic trigonometric functions: 

Very often in trigonometry problems on standardized tests the Pythagorean Theorem is needed to get the final answer.

The Pythagorean Theorem: If a right triangle has legs of length a and b, and a hypotenuse of length c, then c² = a² + b².

Example 3:

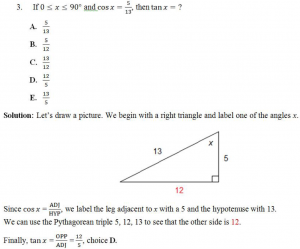
Notes: (1) The most common Pythagorean triples are 3,4,5 and 5, 12, 13. Two others that may come up are 8, 15, 17 and 7, 24, 25.

(2) If you don’t remember the Pythagorean triple 5, 12, 13, you can use the Pythagorean Theorem:

Here we have 5² + b² = 13². Therefore 25 + b² = 169. Subtracting 25 from each side of this equation gives b² = 169 – 25 = 144. So b = 12.

(3) The equation b² = 144 would normally have solutions b = 12 and b = –12. But the length of a side of a triangle cannot be negative, so we reject –12.

More Trigonometry Practice Problems

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Speak to you soon!

Right Triangle Trigonometry

Today I would like to begin talking about right triangle trigonometry. If you will be taking the ACT or one of the SAT math subject tests, and you are going for a very high score, then it is important that you understand the material covered here.

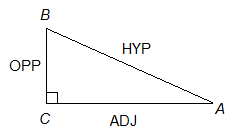
Let’s begin by focusing on angle A in the following picture: 

Note that the hypotenuse is ALWAYS the side opposite the right angle.

The other two sides of the right triangle, called the legs, depend on which angle is chosen. In this picture we chose to focus on angle A. Therefore the opposite side is BC, and the adjacent side is AC. 

Now you should simply memorize how to compute the six trig functions:

Here are a couple of tips to help you remember these:

(1) Many students find it helpful to use the word SOHCAHTOA. You can think of the letters here as representing sin, opp, hyp, cos, adj, hyp, tan, opp, adj.

(2) The three trig functions on the right are the reciprocals of the three trig functions on the left. In other words, you get them by interchanging the numerator and denominator. It’s pretty easy to remember that the reciprocal of tangent is cotangent. For the other two, just remember that the “s” goes with the “c” and the “c” goes with the “s.” In other words, the reciprocal of sine is cosecant, and the reciprocal of cosine is secant.

Note that if you are preparing for the ACT or Level 1 SAT math subject test, then it is not that important for you to know the reciprocal trig functions given in the right hand column, but it also couldn’t hurt to be somewhat familiar with them.

Example 1:

To make sure you understand this, compute all six trig functions for each of the angles (except the right angle) in the triangle below.

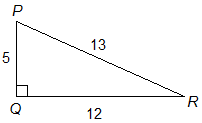
I suggest you try this yourself before looking at the answers:

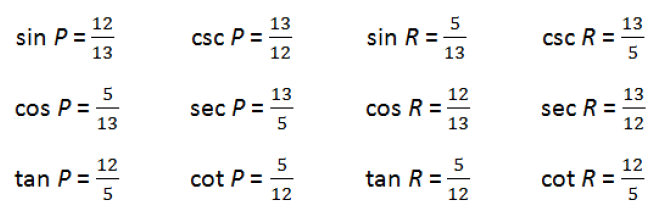
Example 2:

2. In the right triangle pictured below, a, b, and c  and  are the lengths of its sides. What is the value of cos A ?

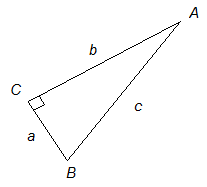
It’s quite easy if you know the rules.

Next week I will continue this thread by providing you with some more difficult examples.

More Trigonometry Practice Problems

If you are preparing for the ACT or an SAT math subject test, you may want to take a look at one of the following books:

If you liked this article, please share it with your Facebook friends:

And if you have any questions on this topic, then please post them on my Facebook wall:

I will answer your questions right away.

Speak to you soon!

The ACT and the SAT

The ACT and SAT are both standardized tests that are used for college admissions. Students should be aware that they have a choice in which standardized test they choose to take. As of 2014, the SAT seems to be the more popular choice on the east and west coasts, and the ACT is more popular throughout the rest of the country (with a few exceptions). But every student should realize that the final decision as to which test to focus on is entirely up to them. This article provides important information about the differences between the two tests so that you can make a more well-informed decision.

Test Length and Structure

The ACT consists of 5 sections. Only 4 of these sections must be completed. The fifth section – writing – is optional. For the required sections, there is a 45 minute english section, a 60 minute math section, a 35 minute reading section, and a 35 minute science section. You are given 30 minutes for the optional writing section. This gives a total required testing time of 45 + 60 + 35 + 35 = 175 minutes, or 2 hours and 55 minutes. With the optional writing section, the total testing time increases to 3 hours and 25 minutes.

The SAT is a longer test than the ACT. It consists of 10 sections, all required. There is one 25 minute essay, one 25 minute writing section, one 10 minute writing section, two 25 minute reading sections, one 20 minute reading section, two 25 minute math sections, one 20 minute math section, and one 25 minute experimental section which may be reading or math. This gives a total testing time of 7(25) + 2(20) + 10 = 225 minutes, or 3 hours and 45 minutes. If we add in the three 5 minute breaks, we get a total time of 4 hours from the beginning to the end of the test.

Note that on the SAT the essay is given at the beginning of the test, it must be completed, and it is factored into the final score.

On the ACT the essay is given at the end of the test, it is optional, and it is NOT factored into the final score.

Scoring

The ACT is graded out of 36 points. The overall score is the average of the scores on each of the 4 required sections. Each of these is also graded out of 36 points.

The SAT is graded out of 2400 points. The overall score is the sum of the scores for reading, writing and math each consisting of a total of 800 points.

Conversion charts are easy to find for comparing ACT and SAT scores. For example, take a look here: ACT/SAT Conversion Chart

Pacing

The ACT requires a faster pace than the SAT to get through each section. Let’s look at math as an example, and assume that a student is pacing themselves to answer every single math question. The student has an average of 1 minute to complete each math question on the ACT, compared to an average of 1 minute and 15 seconds per question on the multiple choice math sections on the SAT.

It should be noted that for many students it may be counterproductive to attempt every question on a standardized test, but this kind of advice lies outside the scope of this article.

Science Section

The ACT has a science section and the SAT does not. It should be noted that the science section is really more about reading comprehension and interpreting data found in charts, figures and tables. Very little knowledge of science is actually required (although it could be argued that students with a stronger science background are at an advantage here).

Free Response Questions

One of the math sections on the SAT has 10 free response questions, also known as “grid-ins.” In these questions the student must give a numerical answer without having any choices to choose from.

Guessing Penalty

The SAT penalizes students for guessing multiple choice questions incorrectly. One quarter of a point is deducted from the student’s raw score for each wrong answer. The final raw score is then rounded to the nearest integer before it is converted to a scaled score. Note that only multiple choice questions have a guessing penalty. There is no penalty for free response questions.

Difficulty versus Trickiness in Math

The ACT tests a few math topics that are more advanced than those found on the SAT, but SAT questions tend to be much trickier. It is often much easier to understand ACT questions upon a first reading, whereas SAT questions tend to seem more confusing at first.

ACT problems tend to be more straightforward, and may be easier for students with stronger algebra skills. On the SAT algebra and messy computations can usually be avoided by “outside the box” thinking.

Mathematics Covered

The ACT covers a few more advanced math topics that never appear on the SAT.

• Basic Trigonometry
• Laws of Sines and Cosines
• Logarithms

In addition, the ACT places a slightly higher emphasis on arithmetic and geometric sequences, complex numbers, rational functions, and basic algebra skills.

Final Note

The best way to decide which test you should focus on is to take a practice test for both the ACT and the SAT. I strongly recommend using official practice tests from the testmakers themselves, preferably an old actual exam from each. Use a score comparison chart to compare your scores and you will see firsthand where your strengths lie.

Once you decide which test you will focus on make sure you take some time to prepare. I always recommend preparing for 10 to 20 minutes per day over a period of 3 to 4 months.

If you decide that you will be taking the SAT, I suggest you take a look at my “Get 800” collection of SAT math prep books, and if you decide that you will be taking the ACT, check out the “ACT Prep Red Book.” Click the picture below for details.

If you liked this article, please share it with your Facebook friends:

Differences Between the ACT and SAT

Informal Algebra

Suppose we are asked to solve for x in the following equation:

x + 3 = 8

In other words, we are being asked for a number such that when we add 3 to that number we get 8. It is not too hard to see that 5 + 3 = 8, so that x = 5.

I call the technique above solving this equation informally. In other words, when we solve algebraic equations informally we are solving for the variable very quickly in our heads. I sometimes call this performing “mental math.”

Algebra The Formal Way

We can also solve for x formally by subtracting 3 from each side of the equation:

x + 3 = 8
     -3   -3
x        = 5

In other words, when we solve an algebraic equation formally we are writing out all the steps – just as we would do it on a test in school.

To save time on the SAT you should practice solving equations informally as much as possible. And although informal skills should take precedence during your SAT prep, you should also practice solving equations formally – this will increase your mathematical skill level.

Another Example

Let’s try another one:

5x = 30

Informally, 5 times 6 is 30, so we see that x = 6.

Formally, we can divide each side of the equation by 5:

5x = 30
5       5
x = 6

A Harder Example

Now let’s get a little harder:

5x + 3 = 48

We can still do this informally. First let’s figure out what number plus 3 is 48. Well, 45 plus 3 is 48. So 5x is 45. So x must be 9.

Here is the formal solution:

5x + 3 = 48
       -3      -3
5x        = 45
5               5
x         =  9

Exercise

Try this one on your own: 3^x + 4 = 31

And feel free to post your explanations in the comments.

If you liked this article, please share it with your Facebook friends:

I’ll see you next week…

Hello everyone.

As some of you know, my best-selling book on Amazon is 320 SAT Math Problems arranged by Topic and Difficulty Level.

One thing that I have noticed is that there are many students that purchase this book that really only want to work on the most difficult problems. It is because of this that I decided to release an abridged version of this book at a lower price.

This new abridged version of the 320 Problems book is called the SAT Prep Book of Advanced Math Problems.

This book contains 192 Level 3, 4, and 5 problems that are uniformly distributed across all topics and each of these three difficulty levels. This book is ideal for students scoring over a 600 that do not feel the need to practice additional Level 1 and 2 Problems. Any students that wish to practice the lower level problems as well should consider purchasing 320 SAT Math Problems arranged by Topic and Difficulty Level instead of this book.

Also remember that I have several other SAT math prep books available. In order for you to decide which of them is the best for you I recommend that you read the following blog post: Which SAT Math Prep Book Should I Use?

And please don’t forget to post any SAT math questions that you are having trouble with on my Facebook wall.

Best of luck to all of you that are taking the SAT. I’ll see you next week with some more great SAT math strategies…