500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Is Your SAT Math Score Above 600 But You Want To Get 800?

“28 SAT Math Lessons to Improve Your Score in One Month – Advanced Course – For Students Currently Scoring Above 600 in SAT Math and Want to Score 800.”

Click the image above to view the book’s page on Amazon.

SAT Exponential Growth Problem with Solution

Today I would like to give a solution to the SAT exponential growth problem presented in this post: Exponential Growth and Decay

Here is the problem once again, followed by a solution.

Level 4 SAT Exponential Growth 

On January 1, 2015, a family living on an island releases their two pet rabbits into the wild. Due to the short gestation period of rabbits, and the fact that the rabbits have no natural predators on this island, the rabbit population doubles each month. If P represents the rabbit population  years after January 1, 2015, then which of the following equations best models the rabbit population on this island over time?

A) P = 2^{t/12 + 1}
B) P = 2^{t + 1}
C) P = 2^12t
D) P = 2^{12t + 1}

Solution using the exponential growth model formula: As seen in example (4) from this post, a quantity that continually doubles over a fixed time period can be modeled by the exponential function P = a(2)^t/d  where a is the quantity at time t = 0, and d is the doubling time in years. In this case, there are initially 2 rabbits, so that a = 2, and the doubling time is every month, or every  1/12  year.

It follows that P = 2(2)^{t ÷ 1/12} = 2(2)^12t = 2¹2^12t = 2^{1 + 12t} = 2^{12t + 1}, choice (D).

Notes: (1) For a review of the laws of exponents used here, see the following post: Laws of Exponents

(2) For additional methods for solving this problem, you may want to take a look at 28 New SAT Math Lessons – Advanced Course

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Exponential Growth and Decay

The current version of the SAT gives problems on exponential growth and decay. Here are the basics that you should know if you want to get a perfect SAT score:

A general exponential function has the form f(t) = a(1 + r)^ct, where a = f(0) is the initial amount and r is the growth rate. If r > 0, then we have exponential growth and if r < 0 we have exponential decay.

Examples: (1) The exponential function  f(t) = 300(2)^t  can be used to model a population with a growth rate of 1 = 100% each year that begins with 300 specimens. The growth rate of 100% tells us that the population doubles each year.

(2) The exponential function  f(t) = 50(3)^2t  can be used to model a population with a growth rate of 2 = 200% every 6 months that begins with 50 specimens. The growth rate of 200% tells us that the population triples. Since c = 2, the tripling occurs every  1/2  year or 6 months.

(3) The exponential function  f(t) = 120(0.75)^t/3  can be used to model a substance which is decaying at a rate of 1 – 0.75 = 0.25 = 25% every 3 years. The initial amount of the substance might be 120 grams. Since c = 1/3, the 25% decay occurs every 3 years.

(4) A quantity that continually doubles over a fixed time period can be modeled by the exponential function f(t) = a(2)^t/d  where a is the quantity at time t = 0, and d is the doubling time in years.

Now try the following SAT math problem. I will post a solution after Thanksgiving, but feel free to post your own solutions in the comments meanwhile.

Level 4 SAT Exponential Growth 

On January 1, 2015, a family living on an island releases their two pet rabbits into the wild. Due to the short gestation period of rabbits, and the fact that the rabbits have no natural predators on this island, the rabbit population doubles each month. If P represents the rabbit population  years after January 1, 2015, then which of the following equations best models the rabbit population on this island over time?

A) P = 2^{t/12 + 1}
B) P = 2^{t + 1}
C) P = 2^12t
D) P = 2^{12t + 1}

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

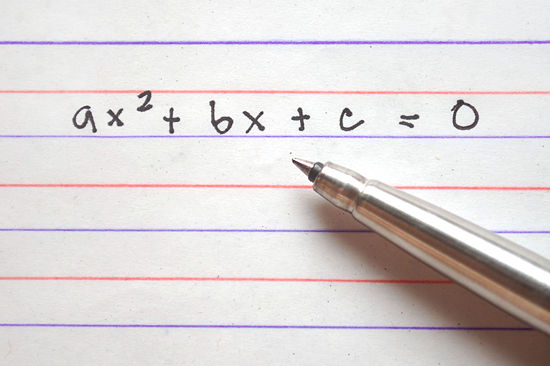
Hard SAT and ACT Math Problem with Solution

Quadratic Equations

Today I would like to provide a solution to yesterday’s hard math problem involving quadratic equations. Here is the problem once again, followed by a solution.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x² – 70x + 25 = 0
B. 49x² + 70x + 25 = 0
C. 49x² + 35x + 25 = 0
D. 49x² + 25 = 0
E. 49x² – 25 = 0

* If -5/7  is the only solution, then x + 5/7  is the only factor (by the factor theorem). So we have

(x + 5/7)(x + 5/7) = 0

x² + 5/7 x + 5/7 x + (5/7)² = 0

x² + 10/7 x + 25/49 = 0

49x² + 70x + 25 = 0

This is choice B.

Notes: (1) The factor theorem says that r is a root of the polynomial p(x) if and only if x – r is a factor of the polynomial.

(2) In factored form, a quadratic equation always has two factors. Since x + 5/7 is the only factor in this problem, it must appear twice.

(3) In going from the first equation to the second equation, we multiplied the two polynomials (x + 5/7  times itself). To do this you can use FOIL or any other method you like for multiplying polynomials.

(4) In going from the second equation to the third equation, we simply added  5/7 x + 5/7 x = 10/7 x.

(5) In going from the third equation to the last equation, we multiplied both sides of the equation by the least common denominator, which is 49. More precisely, on the left hand side we have

49(x² +10/7 x + 25/49)

= 49x² + 49(10/7 x) + 49(25/49)

= 49x² +7(10x) + 25

= 49x² +70x + 25.

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

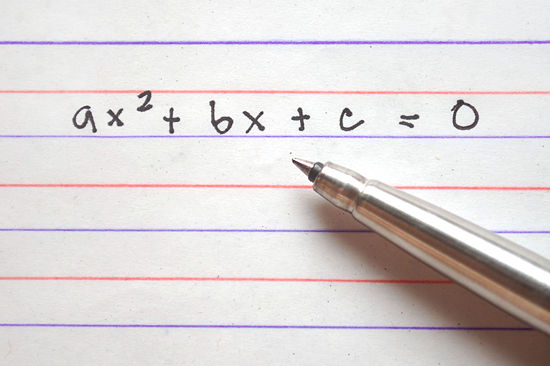
Hard SAT and ACT Math Problem

Quadratic Equations

Today I would like to give a hard math problem involving quadratic equations. This question type can show up on both the SAT and ACT. I will provide a full explanation for this problem soon. Feel free to leave your own solutions in the comments.

Level 5 Quadratic Equations

Which of the following is a quadratic equation that has –5/7 as its only solution?

A. 49x² – 70x + 25 = 0
B. 49x² + 70x + 25 = 0
C. 49x² + 35x + 25 = 0
D. 49x² + 25 = 0
E. 49x² – 25 = 0

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Hard SAT and ACT Math Problem with Solution

System of Inequalities

Today I would like to provide a solution to yesterday’s SAT/ACT problem involving a system of inequalities. Here is the problem once again, followed by a solution.

Level 5 System of Inequalities

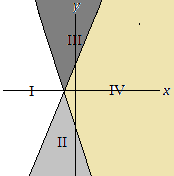
y ≤    2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

Solution: The line y = 2x + 2 has a slope of 2 > 0, and therefore the graph is the line that moves upwards as it is drawn from left to right.

The point (0,0) satisfies the inequality y ≤ 2x + 2 since 0 ≤ 2(0) + 2, or equivalently 0 ≤ 2 is true.

It follows that the graph of y ≤ 2x + 2 consists of sections II and IV.

The line y = –3x – 3 has a slope of –3 < 0, and therefore the graph is a line that moves downwards as it is drawn from left to right.

(0,0) satisfies the inequality y ≥ –3x – 3 since 0 ≥ –3(0) – 3, or equivalently 0 ≥ –3 is true.

It follows that the graph of y ≥ –3x – 3   consists of sections III and IV.

The intersection of the two solution graphs is section IV, choice B.

Note: For a more detailed explanation, see 28 New SAT Math Lessons – Advanced Course

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

Hard SAT and ACT Math Problem

System of Inequalities

Today I would like to give a hard math problem involving a system of inequalities. This type of question can show up on both the SAT and ACT. I will provide a full explanation for this problem tomorrow. In the meantime, feel free to leave your own solutions in the comments.

Level 5 System of Inequalities

y ≤    2x + 2
y ≥ –3x – 3

A system of inequalities and a graph are shown above (the graph is at the top of the post). Which section or sections of the graph could represent all of the solutions to the system?

A. Section I
B. Section IV
C. Sections II and III
D. Sections II and IV
E. Sections I, II and IV

More SAT and ACT Math Problems with Explanations

If you are preparing for the SAT or ACT, you may want to take a look at the Get 800 collection of test prep books.

And if you liked this article, please share it with your Facebook friends:

More On Careless Mistakes & Efficient Prepping

This post is based upon a question I was asked by a student in regards to being able to increase one’s math score by the next SAT.

In the same question the student states that most of his errors are just “careless” mistakes. I redirected him to my article on avoiding careless mistakes, but let me just repost our conversation here as it has information relevant to a lot of other students. I hope you find this useful…

Student: Hi Dr. Steve, I feel as if I have hit a plateau because I can’t really score higher than a 710. I always do practice sections from the College Board Blue Book and miss around 1-2 questions per section. The questions I get incorrect are usually medium questions and not hard. I believe I make careless mistakes… What should I do? I also tend to do A LOT of practice sections. Could this negatively affect my score? I would like to score 750+ (preferably an 800). Is increasing from a 700 to 750+ in just weeks impractical?

Dr Steve: The increase you are looking for is definitely possible. It sounds like all of your prep right now consists of doing practice tests from the College Board’s Blue Book. You should stop this and start prepping in a more efficient way. Now I also need to know what you mean by the word “usually” when you say that you usually get medium questions incorrect. Does that mean on any given practice test you get more medium questions wrong, or that you practically never get hard questions wrong at all? This distinction is important. Let me start with a few suggestions to get you on the right path.

1. If you haven’t done so already, read my article on avoiding careless errors here.
   
2. Go back through all the practice tests you took and start posting up the questions you got wrong here on my Facebook wall. Also explain what the error you made was, no matter how silly or careless you think the errors were. We can then discuss several different ways to solve these problems and how to avoid these errors in the future.
3. Are you proficient in the really basic strategies such as plugging in answer choices, picking numbers, taking guesses, etc. If not, then you need to start practicing lots of problems using these strategies even if you know more efficient ways to solve them. The Intermediate Course from my “28 New SAT Math Lessons” series emphasizes these strategies in a systematic way. The Advanced Course reviews these strategies very quickly in the first lesson, but still gives solutions using these techniques throughout the book. In your case, if you did decide to get one of these, I would probably recommend the Advanced, but make sure you are practicing solving as many of these problems as you can using both basic and advanced strategies. If you choose to continue using only the materials you already have, then again, make sure you are practicing both basic and advanced techniques.
4. Let me emphasize that as you practice solving SAT math questions, try to solve each one in 2 to 4 ways. Possibly using a basic strategy, a more advanced strategy, the way you would do it in school, and/or the quickest way you can think of. Remember – you will never see any specific math problem that you do on your SAT – it’s more important to learn techniques than it is to solve a specific problem.
5. To really improve your score do every problem you get wrong about once per week until you get that question right on your own without making any “careless” errors. Make sure you wait at least several days before reattempting a problem you have gotten wrong. You don’t want to get it right because you recall the mistake you made. You want to get it right because you are no longer falling into the trap you previously fell for.

Student: Well I can confidently say that I know most, if not all, of your strategies (I bought your book and went through the level 5 questions of your book since I got all level 4 questions correct) and that I know all the math involved in most, if not all problems. Out of all the sections I have ever taken, I have only been totally clueless in only like 2 problems. By “usually” I mean I practically never get a hard question wrong unless I make a silly mistake or get tricked, which is quite rare. Since I know not to follow my intuition on hard questions, I tend to check over my work like 2-3 times. On medium questions, however, I tend to work really fast through them. The reason I do this is because it can sometimes take me quite a while to solve some hard questions even if I’m using strategies. Another thing, the way I attack the SAT math section is by just going once through the whole section. Even if I feel that I got all the answers right, I somehow made a mistake in one without noticing. I have question: What is the maximum amount of questions I can miss and still get a 750 or higher? Or does that change from test to test?

Oh wow, I looked back to a problem that I was totally clueless on and solved it in less than 30 seconds.

Dr Steve: To guarantee a 750 you can only get 2 questions wrong. However, the scaling at the high end is very inconsistent, so this varies from test to test.

Based upon your last response, here are a few suggestions:

1. For at least the next week focus on one problem at a time (no full practice tests). Go back and pick out problems that have taken you more than 1 minute. Really take the time to work out the problem several different ways and try to really internalize these methods. Then pay special attention to the one that was quickest.
2. In about a week take another practice test and really focus on NOT RUSHING. Pace yourself correctly meaning if you are working on a problem for about 30 seconds and you’re still confused by it, mark it off and move on – come back to it later – don’t worry – you’ll get to it, and as long as you’re pacing yourself correctly you will have plenty of time to finish the section, go back and work on the ones you skipped, and you may even have several minutes to go back and redo many of the problems one more time. You may want to read this article.”

The student replied that he would look at the additional material.

I wish him and all other students taking the SAT the best of luck in achieving an exceptional math score.

If you are preparing for the SAT, you may want to check out this special deal on all 8 of my SAT math prep books:

Get Eight Books for the Price of Three

If you think your friends might be interested in the information presented here, please share this post with them on Facebook:

Thank you all for your continued support!

Get 800 YouTube Channel Videos

Don’t forget to subscribe to the Get 800 YouTube channel.

On my channel you can find lots of SAT and ACT math prep videos, including solutions to College Board questions, and special promotions.

Here are just a few of the videos you can find on my YouTube channel.

 

 

I hope you find all of my videos useful. I would really appreciate if you would ‘like’ each of the videos, share them, and make comments. Of course, please subscribe to the channel as well.

More On The Triangle Rule

Yesterday we discussed the triangle rule, and I provided a few problems from standardized tests where the triangle rule was extremely useful.  and it was not hard to see how this simple rule should be applied.

Recall that the triangle rule states that that the length of the third side of a triangle is between the sum and difference of the lengths of the other two sides.

This can be written symbolically as “difference < x < sum” where x is the third side of the triangle.

Today let us look at another type of problem that the triangle rule should be used to solve.

Problems involving distances between three points can often be solved using the triangle rule. After all, when you plot three points and look at the distances between each pair of points, you are looking at the lengths of the sides of a triangle.

Try plotting three points on a piece of paper and you you will immediately see what I mean.

There is a small catch however – sometimes when you plot three points, the points can be collinear: that is they all lie on the same line.

This means that the symbol “<” in the triangle rule should be replaced by the symbol “≤.”

In other words, this time we write “difference ≤ x ≤ sum.”

Let’s look at an example that could appear on a standardized math test.

Points Q, R and S lie in a plane. If the distance between Q and R is 18 and the distance between R and S is 11, which of the following could be the distance between Q and S?

A) I only
B) II only
C) III only
D) I and III
E) I, II and III

Solution: Okay, to solve this problem, of course we are going to use the triangle rule… In this case, if Q, R and S form a triangle, then the length of QS is between 18 – 11 = 7 and also 18 + 11 = 29. The extreme cases 7 and 29 form straight lines. In this problem that is fine, so the distance between Q and S is between 7 and 29, inclusive. Thus, the answer is choice (E).

You can see how quickly this problem can be solved when the triangle rule is used.

If you want more practice, then please check out the  Get 800 collection of test prep books. These have more examples of problems that need to use this rule for efficient and correct answering.

And if you liked this article, please share it with your Facebook friends: