500 New SAT Math Problems
Just 19.99 on Amazon

Hi everyone! The latest edition of 500 New SAT Math Problems is now available in paperback from Amazon. This edition just has been modified from the previous edition to account for the changes on the Digital SAT.

The paperback is now on sale on Amazon for only $19.99. Note that once the sale ends (by the end of today), the price of this book will go up to $42.99. 

The promotion has ended. Thanks to everyone who participated. The book is now available at its regular price here: 500 New SAT Math Problems

If you have any questions, feel free to contact me at steve@SATPrepGet800.com 

Thank you all for your continued support!

A Trick For Free Two Day Shipping

I would like to finish this post with a little trick you can use to get free 2 day shipping on any of the books you decide to purchase without making any additional purchases. If you have never used Amazon Prime you can sign up for a free month using the following link.

Sign Up For Amazon Prime For Free

If you have already had a free trial of Amazon Prime you can simply open up a new Amazon account to get a new free trial. It just takes a few minutes! You will need to use a different email address than the one you usually use.

This next part is very important! After you finish your transaction, go to your Account, select “Manage my prime membership,” and turn off the recurring billing. This way in a month’s time Amazon will not start charging you for the service.

After shutting off the recurring billing you will still continue to receive the benefit of free 2 day shipping for one month. This means that as long as you use this new Amazon account for your purchases you can do all of your shopping on Amazon for the next month without having to worry about placing minimum orders to get free shipping.

Just be aware that certain products from outside sellers do not always qualify for free shipping, so please always check over your bill carefully before you check out.

Well I hope you decide to take advantage of this very special offer, or at the very least I hope you will benefit from my Amazon “free 2 day shipping trick.” Here is the link one more time:

Sign Up For Amazon Prime For Free

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Thank you all for your continued support!

The Contrapositive

A statement of the form “if p, then q” is known as a conditional statement. An example of such a statement is “If you are a cat, then you have fur.” Another common way to say this is “All cats have fur.”

There are 3 other statements that often come up in association with a conditional statement. Let’s use the example above to illustrate.

Conditional: If you are a cat, then you have fur.
Converse: If you have fur, then you are a cat.
Inverse: If you are not a cat, then you do not have fur.
Contrapositive: If you do not have fur, then you are not a cat.

The most important thing to know for standardized tests such as the SHSAT is that the contrapositive is logically equivalent to the original conditional statement! The converse and inverse are not.

For example, suppose the conditional statement “All cats have fur” is true. You may want to rewrite this as “If you are a cat, then you have fur.” It follows that “If you do not have fur, then you are not a cat” is also true.

In particular, if you are given the statement “Skittles does not have fur,” you can infer “Skittles is not a cat.”

Note that neither the converse nor the inverse is logically equivalent to the original conditional statement, but they are equivalent to each other.

Example 1

All of Jim’s friends can ski.

If the statement above is true, which of the following statements must also be true?

(A) If John cannot ski, then he is not Jim’s friend
(B) If Jeff can ski, then he is not Jim’s friend.
(C) If Joseph can ski, then he is Jim’s friend.
(D) If James is Jim’s friend, then he cannot ski.
(E) If Jordan is not Jim’s friend, then he cannot ski.

Solution: The given statement can be written in conditional form as “If you are Jim’s friend, then you can ski.” The contrapositive of this statement is “If you cannot ski, then you are not Jim’s friend. Replacing “you” with “John” gives the correct answer as choice (A).

Example 2

If a beverage is listed in menu A, it is also listed in menu B.

If the statement above is true, which of the following statements must also be true?

(A) If a beverage is listed in menu B, it is also in menu A.
(B) If a beverage is not listed in menu A, it is not listed in menu B.
(C) If a beverage is not listed in menu B, it is not listed in menu A.
(D) If a beverage is not listed in menu B, it is in menu A.
(E) If a beverage is listed in menu B, it is not listed in menu A.

Solution: Simply observe that the statement in choice (C) is the contrapositive of the given statement. So the answer is choice (C).

Conclusion

If you understand how to identify the contrapositive of a conditional statement, then you will be able to easily get most logic questions correct that appear on standardized tests.

If you will be taking the ACT, you may want to check out my series of ACT math prep books:

If you liked this article, please share it with your Facebook friends:

Heart of Algebra Problem with Solution

from 320 SAT Math Problems

Today I’d like to provide you with a solution to the last Heart of Algebra problem I gave you. Here is the question one more time, followed by a complete explanation.

Level 4 Heart of Algebra

2x + 5 + k = 7x
2y + 5 + t = 7y

In the equations above, k and t are constants. If t is k minus 1/3, which of the following is true?

(A) x is y minus 1/3
(B) x is y minus 1/15
(C) x is y plus 1/3
(D) x is y plus 1/15

* Solution using the elimination method: We begin by replacing t by k – 1/3, and interchanging the order of the two equations.

2y + 5 + k – 1/3 = 7y

2x + 5 + k          = 7x

We then subtract the bottom equation from the top equation.

2y – 2x – 1/3 = 7y – 7x

We solve this equation for x by adding 7x, subtracting 2y, and adding  1/3  to each side of the equation,

5x = 5y + 1/3

Finally, we multiply each side of this last equation by  1/5  to get

x = 1/5 (5y + 1/3) = 1/5 ⋅ 5y + 1/5 ⋅ 1/3 = y + 1/15

So x is y plus 1/15, choice D.

If you liked this post, please share it with your Facebook friends:

And don’t forget to check out my social media pages:

320 SAT Math Problems

The promotion has ended. Thanks to all of you that participated. Click on the following image for a very special offer on the Get 800 collection of SAT math books.

If you think your friends might be interested in this special offer, please share it with them on Facebook:

Heart of Algebra Problem

from 320 SAT Math Problems

Today I’d like to give you a problem from 320 SAT Math Problems arranged by Topic and Difficulty Level. This one is a Level 4 Heart of Algebra problem. I will provide a solution tomorrow.

Level 4 Heart of Algebra

2x + 5 + k = 7x
2y + 5 + t = 7y

In the equations above, k and t are constants. If t is k minus 1/3, which of the following is true?

(A) x is y minus 1/3
(B) x is y minus 1/15
(C) x is y plus 1/3
(D) x is y plus 1/15

If you liked this post, please share it with your Facebook friends:

And don’t forget to check out my social media pages:

 

Hard Problem with Solution

from 320 SAT Math Problems

Today I’d like to provide you with solutions to the difficult Passport to Advanced Math problem I posted yesterday. This problem is from the new edition of 320 SAT Math Problems. You can click the image of the book above to view the book on Amazon. Here is the problem one more time with two complete solutions.

Level 5 Passport to Advanced Math

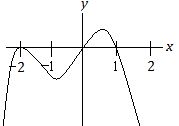
Which of the following could be an equation for the graph shown in the xy-plane above?

(A) y = x(x + 2)(1 – x)
(B) y = x²(x + 2)(x – 1)
(C) y = x(x + 2)²(1 – x)
(D) y = x²(x + 2)³(x – 1)²

Solution by process of elimination: The answer choices show us that the answer must be a polynomial.

Since there are 3 turning points, the polynomial must have degree at least 4. We can therefore eliminate choice A (this polynomial has degree 3).

Since both “ends” of the graph go in the same direction (they both tend to –∞), the polynomial must have even degree. This eliminates choice D (this polynomial has degree 7). Note that we can also use this same reasoning to eliminate choice A.

We can eliminate choice B by observing that if we plug a very large value of x into y  = x²(x + 2)(x – 1), we will get a large positive value for y. But according to the graph we should get a negative value for y (since the graph is below the x-axis for large x).

So the answer is choice C.

Notes: (1) A polynomial has the form a_nxⁿ + a_n-1 x^n-1 + ⋅⋅⋅ + a₁x + a₀ where a₀, a₁, … , a_n are real numbers. For example, x² + 2x – 35 is a polynomial.

The degree of the polynomial is n. In other words, it is the highest power that appears in the expanded form of the polynomial.

(2) If a polynomial is in factored form, then we can get the degree of the polynomial by adding the degrees of the factors.

For example, the polynomial in choice A has degree 1 + 1 + 1 = 3.

Similarly, the polynomials in choices B, C and D have degrees 4, 4 and 7, respectively.

(3) The “end behavior” of the graph of a polynomial can tell you whether the polynomial has even or odd degree. If both ends of the graph head in the same direction (both up to ∞, or both down to –∞), then the polynomial must have even degree. If the ends head in different directions (one up and the other down), then the polynomial must have odd degree.

The graph shown in this problem is therefore for an even degree polynomial.

(4) The degree of a polynomial is at least one more than the number of “turning points” on its graph.

Since the graph in this problem has 3 turning points (at x = –2, –1, and approximately  1/2), the degree of the polynomial must be at least 4.

(5) Putting notes (3) and (4) together, we see that the possible degrees for the polynomial whose graph is shown are 4, 6, 8,…

* Quick solution: Since the graph does not pass through the x-axis at the zero x = –2, it follows that –2 is a zero with even multiplicity. Equivalently, the factor (x + 2) must appear an even number of times (or equivalently, it must have an even power). This eliminates choices A, B and D. So the answer is choice C.

Notes: (1) c is a zero of a polynomial p(x) if p(c) = 0. For example, all of the polynomials in the answer choices have the same zeros. They are –2, 0 and 1.

(2) p(c) = 0 if and only if x – c is a factor of the polynomial p(x).

(3) The multiplicity of the zero x is the degree of the factor x – c.

For example, in choice D, 0 and 1 have multiplicity 2, and –2 has multiplicity 3.

(4) If a zero c of a polynomial has odd multiplicity, then the graph of the polynomial passes through the x-axis at x = c.

From the graph given, we see that 0 and 1 are zeros of the polynomial with odd multiplicity.

(5) If a zero c of a polynomial has even multiplicity, then the graph of the polynomial touches the x-axis at x = c, but does not pass through it.

From the graph given, we see that –2 is a zero of the polynomial with even multiplicity.

(6) It might be tempting to try to plug in the zeros to try to eliminate answer choices in this problem. Unfortunately, all of the answer choices have polynomials with the same zeros.

If you liked this post, please share it with your Facebook friends:

And don’t forget to check out my social media pages:

 

Hard Problem From 320 SAT Math Problems

Today I’d also like to give you a difficult Passport to Advanced Math problem right from 320 SAT Math Problems arranged by Topic and Difficulty Level. Feel free to post your attempted solutions in the comments. I will provide my own solutions tomorrow.

Level 5 Passport to Advanced Math

Which of the following could be an equation for the graph shown in the xy-plane above?

(A) y = x(x + 2)(1 – x)
(B) y = x²(x + 2)(x – 1)
(C) y = x(x + 2)²(1 – x)
(D) y = x²(x + 2)³(x – 1)²

If you liked this post, please share it with your Facebook friends:

And don’t forget to check out my social media pages:

320 SAT Math Problems – Free Sample

The new edition of 320 SAT Math Problems arranged by Topic and Difficulty Level is almost ready. I will be releasing it in about a week at a promotional price of about $5.50. If you want to take advantage of this low price, make sure to get on the notification list by sending an email to  steve@SATPrepGet800.com with “Notify me” written in the subject line.

While you are waiting for the book to arrive, I have put together a free sample for you. Click the following link to open up the free sample in your browser. You can then save it to your computer or print it out if you wish:

320 SAT Math Problems – Free Sample

Take a look at my product page to see all of the other books from the Get 800 collection: Get 800 Product Page

If you think your friends might be interested in being notified of this special offer, please share it with them on Facebook:

Thank you all for your continued support!

Distance Rate Time Charts

Yesterday we discussed how to solve a certain type of rate problem very quickly simply by plugging numbers into a simple formula. In case you are interested you can find that post here: Xiggi’s formula.

In yesterday’s post we learned that Xiggi’s formula can be used to find an average rate when two individual rates for the same distance are known.

But what if we want to find the distance or time instead?

If the two distances are the same, then Xiggi’s formula can still be used but the solution will require a little more work. In this case however Xiggi’s formula is probably not the most efficient way to solve the problem.

Also, what if we want to solve a rate problem where the two (or more) distances are different?

Well in this case we certainly cannot use Xiggi’s formula. Another method will be needed.

In this blog post I would like to go over a method of solution that will work for any math problem involving distances, rates and times that show up on standardized tests such as the SAT, ACT and GRE. Today we will carefully go over how to set up a “distance = rate · time” chart.

Let’s start right away with an example.

Marco drove from home to work at an average speed of 50 miles per hour and returned home along the same route at an average speed of 46 miles per hour. If his total driving time for the trip was 4 hours, how many minutes did it take Marco to drive from work to home?

Let’s solve this problem by writing out a “distance = rate · time” chart.

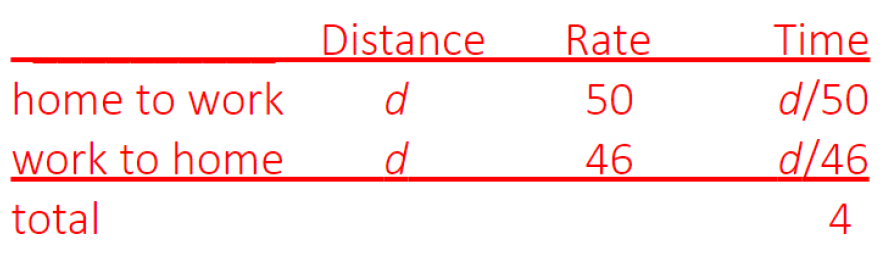
Note that although we do not know either distance, we do know that they are the same, so we can call them both “d.” Also, since

distance = rate · time,

we have that

We use this to get the first two entries in column three. The total time is given in the question. So we have

46d + 50d  = 4 · 50 · 46

96d = 4 · 50 · 46

We want the time it takes Marco to drive from work to home, that is we want to compute d/46.

In hours, this is equal to

To convert to minutes we multiply by 60.

Let’s also try to solve this problem using Xiggi’s formula.

We have

Finally to convert from hours to minutes we multiply by 60 and get 125.

Notice that this particular problem was not so straightforward to solve using Xiggi’s formula. Compare this to the problem in yesterday’s blog post. Do you see the difference? In last week’s question we were being asked to find a rate, whereas in this question we were asked to find a time.

Toward the end of yesterday’s post you were asked to solve the following problem:

Jason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?

Let’s first solve this problem using Xiggi’s formula.

So we can grid in 8.55 or 8.56.

And now here is a solution using a “distance = rate · time” chart.

So we grid in 8.55 or 8.56.

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

Xiggi’s Formula – An Advanced Math Strategy

Hello everyone. This post is mostly for more advanced students that are trying to get an 800 in SAT math (or close to it). That said, the strategy I will be describing here is actually very easy to apply. So even if you are not going for an 800, it will not take too much effort to learn this technique.

Today I would like to talk about Xiggi’s formula.

First of all, some of you may want to know who Xiggi is. Well Xiggi is a frequent poster on the SAT preparation forum of College Confidential.  If you are preparing for the SAT I highly recommend that you utilize this forum as a resource.

The formula I will be discussing in this post is actually called the harmonic mean formula, but on the College Confidential site we all call it Xiggi’s formula. The reason for this is because Xiggi has become well known for helping students on the forum to solve this particular type of problem.

So when should one use Xiggi’s formula? Well, Xiggi’s formula can be used to find an average rate when two individual rates for the same distance are known.

Here is the formula:

Important notes:  (1) Xiggi’s Formula works only when the two distances are the same.

(2) Even though the distance is often given in these types of problems, note that the formula does not use the distance. It uses only the two rates.

(3) For these types of SAT problems, the words “rate” and “speed” are interchangeable.

Here is an example of a problem where Xiggi’s formula is the best way to go:

An elephant traveled 7 miles at an average rate of 4 miles per hour and then traveled the next 7 miles at an average rate of 1 mile per hour. What was the average speed, in miles per hour, of the elephant for the 14 miles?

Let’s solve this problem using Xiggi’s formula. We have

Just to compare, let’s also solve this problem in the more traditional way – by writing out a “distance = rate · time” chart.

Note that we computed the times by using “distance = rate · time” in the form

Finally, we use the formula in the form

Note: To get the total distance we add the two distances, and to get the total time we add the two times. Be careful – this doesn’t work for rates!

SAT, ACT and GRE math problems of this type are always Level 5 problems. But if you know Xiggi’s formula, you can solve this type of question in just a few seconds. So in my opinion, it is well worth committing this one to memory.

Here is another math question where Xiggi’s formula can be useful. Give this one a try on your own.

Jason ran a race of 1600 meters in two laps of equal distance. His average speeds for the first and second laps were 11 meters per second and 7 meters per second, respectively. What was his average speed for the entire race, in meters per second?

See if you can solve this problem using Xiggi’s formula. And then also try to solve it with a “distance = rate · time” chart.

I will provide both solutions in tomorrow’s post. But feel free to leave your own solutions in the comments.

Remember that Xiggi’s formula should only be used when the two distances are the same! Should it ALWAYS be used when the distances are the same? We will address this question in next week’s post where we will look at distance, rate, time problems where Xiggi’s formula is not as useful.

Until then, I will leave you with the following “Challenge Problem.”

Use the formula d = rt to derive Xiggi’s formula.

More Hard Practice Problems

For many more hard problems like these, each with several fully explained solutions, check out the Get 800 collection of test prep books. Click on the picture below for more information about these books.

If you liked this article, please share it with your Facebook friends:

Speak to you soon!

Hard GRE Math Arithmetic Problems with Solutions

Yesterday I posted some really hard GRE Arithmetic problems, and today I would like to give you solutions to those problems. Please feel free to post your own solutions or attempted solutions in the comments below as well. If you still want further explanation after reading the below solutions please do not hesitate to ask.

Level 5 GRE Arithmetic Problems with Solutions

1. If n is a positive integer such that the units (ones) digit of n² + 4n is 7 and the units digit of n  is not 7, what is the units digit of n + 3?

Solution: By plugging in values for n, we find that for n = 9,

n² + 4n = 92 + 4 ⋅ 9 = 81 + 36 = 117.

So n = 9 works, and n + 3 = 9 + 3 = 12. So the units digit of n + 3 is 2.

Advanced solution showing the independence of n:

n² + 4n = n(n + 4).

So we are looking at positive integers 4 units apart whose product ends in 7. Since 7 is odd, n must be odd. So n must end in 1, 3, 5, or 9. Note that we skip n = 7 since the problem forbids us from using it.

If n ends in 1, then n + 4 ends in 5, and n(n + 4) ends in 5.
If n ends in 3, then n + 4 ends in 7, and n(n + 4) ends in 1.
If n ends in 5, then n + 4 ends in 9, and n(n + 4) ends in 5.
If n ends in 9, then n + 4 ends in 13, and n(n + 4) ends in 7.

So n ends in a 9, and n + 3 ends in a 2.

2. The sum of the positive odd integers less than 200 is subtracted from the sum of the positive even integers less than or equal to 200. What is the resulting difference?

We write out each sum formally, line them up, and subtract term by term.

2 + 4 + 6 + … + 200
1 + 3 + 5 + … + 199
1 + 1 + 1 + … + 1

Now notice that we’re adding 1 to itself 100 times. So the answer is 100.

Note: It is easiest to see that we are adding 100 ones by looking at the sum of the positive even integers less than or equal to 200. There are 200/2 = 100 terms in this sum.

Quick solution: Once you get a little practice with this type of problem you can simply compute 100•1 = 100.

Solution using the sum feature on your graphing calculator: (This solution cannot be used on the GRE, but it could for other standardized tests where a graphing calculator is allowed) Press the 2nd button followed by the List button (same as Stat button).
Go to Math and select 5: sum( or press 5.
Press 2nd followed by List again.
Go to Ops and select 5: seq( or press 5.
Enter x, x, 1, 199, 2)).
The display should look like this: sum(seq(x, x, 1, 199, 2)).
Press Enter and you should get the answer 10,000.
Next enter sum(seq(x, x, 2, 200, 2)) and you should get the answer 10,100. Finally, 10,100 – 10,000 = 100.

Note: In the expression sum(seq(x, x, 2, 200, 2)) the last 2 indicates the step size. Here we are adding every other number.

3. The positive number k is the product of four different positive prime numbers. If the sum of these four prime numbers is a prime number greater than 20, what is the least possible value for k?

Solution: Let’s begin listing sequences of 4 prime numbers, and checking if their sum is also prime, beginning with the smallest primes.

2, 3, 5, 7          Sum = 17      too small
2, 3, 5, 11        Sum = 21      not prime
2, 3, 7, 11        Sum = 23      prime
2, 3, 5, 13        Sum = 23      prime

Now, (2)(3)(7)(11) = 462, and (2)(3)(5)(13) = 390. Since 390 is smaller,  k = 390.

More Hard GRE Math Practice Problems

For many more hard GRE math problems like these, each with several fully explained solutions, check out 320 GRE Math Problems arranged by Topic and Difficulty Level. 

And if you think your friends would like to try these problems, please share:

Talk soon!